Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Лубенцова Е.В. 1 Ожогова Е.В. 1 Лубенцов В.Ф. 1 Шахрай Е.А. 1 Масютина Г.В. 2

---

1 ФГБОУ ВО «Кубанский государственный технологический университет»

2 Институт сервиса, туризма и дизайна (филиал) ФГАОУ ВО «Северо-Кавказский федеральный университет»

Проведен анализ оценивания отношения согласованности при обработке информации матриц парных сравнений. Учитывая независимость высказываемых экспертами суждений при индивидуальном подходе заполнения матриц, необходимым условием дальнейшей обработки информации является проверка выставленных ими оценок на непротиворечивость. В практических задачах эту проверку производят по величине отношения согласованности, которое считают показателем качества совокупности экспертных оценок. Однако в случае несогласованности мнений экспертов не существует единого правила корректировки значений элементов матрицы. Целью данной работы является разработка метода достижения согласованности матриц парных сравнений на основе корректировки их собственных значений. Положительным моментом метода является отсутствие необходимости пересмотра всех значений матрицы для улучшения ее согласованности. Сущность метода основана на анализе компонентов максимального собственного значения матрицы. Численными примерами показано, что чем больше отклонение i-й компоненты от единицы, тем больше влияние i-го элемента в комплексе всех элементов матрицы на ухудшение согласованности. Наличие такого свойства делает удобным использование отношения согласованности для проверки качества экспертных оценок. Метод не вызывает затруднений при программной реализации в составе алгоритмов решения задач выбора и сравнения альтернатив для поддержки принятия решения. Экспериментальные исследования предложенного метода подтвердили его правомочность для проверки качества экспертных оценок.

Статья в формате PDF

0 KB

отношение согласованности

матрица парных сравнений

экспертные оценки

наибольшее собственное значение матрицы

1. Саати Т.Л. Принятие решений при зависимостях и обратных связях: аналитические сети. М.: ЛИБРОКОМ, 2009. 360 с.

2. Саати Т.Л. Принятие решений. Метод анализа иерархий. М.: Радио и связь, 1993. 320 с.

3. Тихомирова А.Н., Сидоренко Е.В. Модификация метода анализа иерархий Т. Саати для расчета весов критериев при оценке инновационных проектов // Современные проблемы науки и образования. 2012. № 2. [Электронный ресурс]. URL: http://science-education.ru/ru/article/view?id=6009 (дата обращения: 24.05.2020).

4. Анализ согласованности матриц парных сравнений на основе их собственных чисел [Электронный ресурс]. URL: https://studme.org/279799/informatika/analiz_soglasovannosti_ matrits_parnyh_sravneniy_osnove_sobstvennyh_chisel (дата обращения 24.05.2020).

5. Системы поддержки принятия решения / Под ред. В.Г. Халина, Г.В. Черновой. М.: Изд-во Юрайт, 2017. 494 с.

6. Бугаев Ю.В., Медведкова И.Е., Бабаян М.К. Методы проверки транзитивности индивидуальных экспертных предпочтений // Вестник ФГУНТ. 2014. № 2. С. 77–82.

7. Огурцов А.Н., Староверова Н.А. Алгоритм повышения согласованности экспертных оценок в методе анализа иерархий // Вестник «ИГЭУ». 2013. Вып. 5. С. 81–84.

Многие аналитические задачи выбора и сравнения альтернатив требуют использования независимых суждений (мнений), что может быть достигнуто только привлечением экспертов. Эти суждения должны быть непротиворечивы, т.е. выставленные ими оценки (баллы) должны быть проверены на согласованность и только после этого информацию, полученную от экспертов, можно считать приемлемой для принятия решений.

Область применения экспертных методов в анализе достаточно широка. К наиболее распространенным можно отнести следующие задачи:

– определение альтернативных вариантов решения проблемы (задачи) с оценкой их предпочтения;

– определение и ранжирование по заданному критерию наиболее существенных факторов, влияющих на выбор и сравнение альтернатив;

– выявление рисков в управлении процессами и производствами;

– определение потенциально опасных производственных объектов для построения рациональных схем противоаварийной защиты, например в нефтепереработке, нефтехимии, и другие.

Более простыми, но менее надежными методами опроса экспертов по сравнению с коллективными, являются индивидуальные методы. Они позволяют эксперту высказывать свое мнение независимо от других. Однако при этом требуется согласование мнений всех экспертов. После сбора информации используются различные методы обработки данных. Одним из распространенных является метод парных сравнений [1]. В этом случае каждый эксперт оформляет свой результат в форме квадратной матрицы, элементы которой формируются по шкале относительной важности [2].

В практических задачах согласованность матрицы парных сравнений может не достигаться, поскольку суждения эксперта нельзя выразить точной формулой. При заполнении матрицы эксперт пользуется оценками относительной важности предпочтений по шкале интенсивности от 1 до 9 [3], которые без дополнительной корректировки могут приводить к несогласованности. Несогласованность матрицы парных сравнений может быть вызвана как личными предпочтениями эксперта, так и степенью неопределенности объекта оценки. Поэтому несогласованность матрицы является результатом взаимодействия этих факторов. Поскольку неопределенность является свойством изучаемого объекта оценки, то величину отношения согласованности (ОС) можно считать показателем качества совокупности экспертных оценок. Если для матрицы парных сравнений ОС превышает пороговое значение (>10 %), то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы. В этом случае эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить ее согласованность. Значение ниже порогового (< 10 %) считается допустимым, т.е. отклонения элементов матрицы парных сравнений от приемлемых величин не столь велики, чтобы заметно нарушить согласованность. По результатам заполнения матрицы экспертные оценки, как правило, подлежат проверке. Для этого обычно применяются различные числовые индексы, разработанные как для групповых, так и для индивидуальных опросов, но единого правила выбора такого индекса пока нет [4]. Так, например, эксперт может изменить попарные оценки сравнения методом перебора, однако правила по изменению одной или одновременно нескольких оценок пока нет. Причем недостатком метода перебора значений всех элементов матрицы является то, что в нем не находит своего отражения варьирование наиболее значимых элементов матрицы. Поэтому вопрос о достижении наименьшего значения ОС является актуальным.

Формулировка цели и постановка задачи

Целью данной работы является разработка метода достижения согласованности матриц парных сравнений на основе корректировки их собственных значений, а также реализация его в алгоритме сравнения альтернатив, выполняемом экспертами или одним экспертом. Поставленная цель требует решения задачи по обоснованию предложенного условия и использованию его для корректировки компонентов максимального собственного значения матрицы. Использование результатов решения данной задачи позволит учитывать суждения эксперта и провести более тонкое ранжирование рассматриваемых альтернатив по степени предпочтительности [5]. В конечном итоге применение метода будет способствовать повышению эффективности принятия решений при оценке перспективности и реализуемости инновационных проектов [6, 7].

Метод достижения согласованности матриц парных сравнений на основе корректировки их собственных значений

Поскольку человеческие ощущения нельзя выразить точной формулой, то при сравнении нескольких объектов транзитивная (порядковая) и кардинальная (количественная) однородности могут быть нарушены. Для оценки однородности суждений в методе парных сравнений после заполнения матрицы определяются веса факторов и находится приоритет фактора, рассчитываются наибольшее собственное значение матрицы λ_max, индекс согласованности (ИС) и отношение согласованности (ОС). Суждения экспертов считаются непротиворечивыми, если ОС < 10 % [1]. Индекс согласованности определяется по формуле [3]:

ИС = (λ_max – n)/(n – 1),

где λ_max – наибольшее собственное значение обратно симметричной матрицы; n – количество столбцов и строк матрицы.

Максимальное (наибольшее) собственное значение λ_max определяется по формуле

λ_max = λ_1max + λ_2max + … + λ_{n max} =

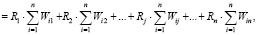
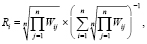
где λ_{i max} – компоненты максимального (наибольшего) собственного значения матрицы; i – индекс строки матрицы, i = 1,2, … n; j – индекс столбца матрицы, j = 1,2, … n; Wij – экспертные оценки.

Отношение согласованности вычисляют делением ИС на величину случайного индекса (СИ) матрицы соответствующего порядка по формуле [1]:

ОС = ИС/СИ.

В нашем случае всегда λ_max > n. Отсюда следует, что при невыполнении согласованности хотя бы одна из компонент максимального собственного числа матрицы λ_{i max} будет больше остальных и будет приводить к нарушению условия (λ_max – n) = 0. Тогда для достижения согласованности суждений эксперта необходимо найти максимальное отклонение компоненты λ_{i max} от единицы, т.е. max /?i /= /1– ?i max / и использовать это отклонение для корректировки первоначальной оценки, введенной экспертом. Это может быть записано в виде условия

max/?/ = /1– ?i max / > aij .

Чем больше отклонение ?i i-й компоненты от единицы, тем больше влияние i-го элемента в комплексе всех элементов матрицы на ухудшение согласованности. Наличие такого свойства делает удобным использование ОС для проверки качества экспертных оценок, особенно при программной реализации данной методики. Как показывают нижеприведенные примеры, выполнение условия ?i = min (/1– ?i max /) позволяет получить значение ОС < 10 % и далее минимизировать его.

Экспериментальные исследования предложенного метода

Рассмотрим матрицу парных сравнений 5х5 с числовыми оценками для критериев A, B, C, D, E, приведенную в табл. 1.

Используя рассчитанные оценки критериев (табл. 1), получено отношение согласованности ОС1 = 13,68 % для матрицы А1, которое не является приемлемым, т.е. уровень согласованности очень мал. Требуется, чтобы ОС было меньше 10 %. Необходимо скорректировать приведенную матрицу суждения. Значение максимальной составляющей равно ?3max = 1,6789 (в табл. 1 выделено темным цветом), максимальное отклонение равно ?i = 0,6789, что указывает на необходимость корректировки третьего элемента первой строки матрицы в табл. 1, т.е. a13 = 5. Уменьшим значение a13 на единицу. Матрица с корректированным значением a13 приведена в табл. 2.

Результаты, полученные аналогичными вычислениями, показывают, что коррекция элемента a13 позволила уменьшить ОС в 1,34 раза. Проводя дальнейшие вычисления, получены следующие результаты, характеризующие уменьшение ОС:

при a13 = 3, ? i max = {0,9591163; 0,9617182; 1,365; 1,069; 0,946},

max /?/ = max{0,0222681; 0,044684; 0,52344; 0,06166; 0,06007} = 0,52344,

ОС2 = 6,71 %;

при a13 = 2, ? i max = {0,9451337; 0,9674979; 1,205521; 1,075; 0,952},

max /?/ = max{0,0548663; 0,032502; 0,205521; 0,075199; 0,048085} = 0,205521,

ОС3 = 3,24 %;

при a13 = 1, ? i max = {0,9683669; 0,9683669; 1,06025; 1,076164; 0,953},

max /?/ = max{0,031633; 0,031633; 0,060205; 0,076164; 0,04723} = 0,076164,

ОС4 = 0,58 %.

Таблица 1

Числовые оценки матрицы парных сравнений А1 для критериев

Таблица 2

Числовые оценки матрицы парных сравнений А2 с корректированным значением третьего элемента в первой строке

Следует заметить, что, несмотря на улучшение ?max в 23,5 раза, корректировка осуществлялась только на один из элементов матрицы a13, что, в общем случае, могло нарушить исходную ранжировку качественных предпочтений эксперта в сторону, отличную от реальной ситуации. Для устранения такого недостатка, т.е. для исключения нарушения логичности суждений эксперта, проведем анализ согласованности матрицы парных сравнений на основе перебора различных компонент ее максимального собственного числа. Пусть матрица 5?5 определена выражением, представленным в табл. 3. Отношение согласованности ОС1 = 15,32 % > 10 %, что является неприемлемым и свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, т.е. уровень их согласованности очень мал. Вторая компонента максимального собственного числа равна ?2max = 1,6324 и указывает на необходимость корректировки второго элемента в первой строке матрицы a12 (табл. 3). Последовательное изменение aij приводит к улучшению ОС, что подтверждено полученными следующими данными:

при max /?/ = 0,398, a15 = 5, ОС = 10,93 %;

при max /?/ = 0,396, a12 = 3, ОС = 11,0 %:

при max /?/ = 0,405, a15 = 4, ОС = 6,82 %;

при max /?/ = 0,369, a15 = 3, ОС = 7,2 %.

Анализ согласованности матриц парных сравнений показал, что дальнейшее изменение значений ее элементов приводит к незначительному изменению ОС, всего лишь в 6,98/6,82 = 1,02 раза, и позволяет остановиться на матрице табл. 4.

Судя по нормализованным оценкам векторов, данный вариант матрицы не нарушает логичности первоначальных суждений эксперта для критериев С, D, Е и ранжирования качественных предпочтений. Причем в данном варианте матрицы по сравнению с матрицей, имеющей ОС = 6,98 %, исключается компромисс между суждениями, так как лингвистическая оценка предпочтений согласно девятибалльной шкале записана нечетными числами, а не промежуточными (четными). Рисунок иллюстрирует результаты минимизации ОС при последовательной корректировке значений оценок для двух элементов матрицы сравнений пяти критериев при использовании шкалы от 1 до 9.

Таблица 3

Числовые оценки матрицы парных сравнений А3 для критериев

Таблица 4

Числовые оценки матрицы парных сравнений А4 для критериев

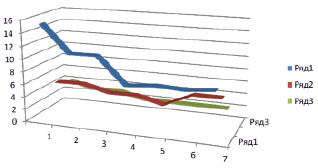
График минимизации ОС (ряд 1) c использованием значений а15 = (5, 5, 4, 4, 3, 5, 6), (ряд 2) и а12 = (4, 3, 3, 2, 2, 2, 2) (ряд 3) в интервале экспертных оценок аij = [1-7]: по оси абсцисс – значения ОС

Установлено, что при отклонении суждений эксперта от однородности одна из компонент собственных значений матрицы будет больше единицы. Таким образом, для достижения необходимой согласованности суждений эксперта необходимо использовать отклонение (1 – ?i max). Результаты исследования показали, что коррекция элемента матрицы, соответствующего максимальному значению компонента максимального собственного значения матрицы, позволяет уменьшить ОС. Если использовать воздействие на различные компоненты максимального собственного числа матрицы, то можно достигнуть не только приемлемого значения ОС, но и осуществить минимизацию ОС, поскольку дальнейшее изменение значений ее элементов не приводит к значительному изменению ОС.

Заключение

В данной статье предложен метод достижения приемлемой согласованности при решении задачи сравнения нескольких вариантов на основе экспертных оценок. Суть метода состоит в том, что в диалоге с компьютером лицо, принимающее решение, либо компьютерная программа, на основе анализа компонент максимального собственного числа матрицы изменяет оценки значимости критериев таким образом, чтобы получить наименьшее значение отношения согласованности. Корректировка оценки осуществляется по следующему принципу: вычисляется отклонение i-й компоненты от единицы и чем больше модуль отклонения, тем меньший приоритет выставляется элементу аij в матрице. С помощью предложенного метода осуществлен сравнительный анализ пяти вариантов. Показано, что использование данной методики позволяет целенаправленно проводить корректировку экспертных оценок, обеспечивая более грамотную ранжировку качественных предпочтений лица, принимающего решение.

Библиографическая ссылка