Подсчет запасов углеводородов выполняется в условиях неопределенности геофизических данных, что приводит к необходимости определения достоверности подсчитанных параметров. Оценка достоверности служит инструментом, который позволяет определять коммерческие риски разработки месторождений [1, 2].
Традиционно для оценки достоверности геологических моделей и определения рисков бурения планируемых скважин используется метод перекрестной проверки (также известный как кросс-проверка, cross-validation) или метод стохастического моделирования, позволяющий оценивать неопределенность (uncertainty assessment) [3]. Оба метода основаны на концепции, что все проблемы неоднородности заключены в данных, заданных с ошибкой. Чтобы уйти от этой концепции и включить в правила преобразования данных возможность того, что сами эти правила зависят от особенностей данных, следует использовать методы нечеткого прогнозирования. Предложенные методы позволяют выполнять построение нечетких петрофизических моделей, которые отражают нечеткость исходных данных [4].
Согласно теории нечеткого моделирования, рассмотренной в статье [5], оптимальной моделью для представления исходных петрофизических взаимосвязей в форме функции принадлежности является экспоненциальная модель. Но ранее использовались данные, полученные в результате петрофизических исследований, которые образовывали полигон рассеяния и не анализировались связи, заданные аналитически, что и является предметом данной статьи.
Цель исследования: рассмотреть и провести сравнительный анализ математических методов построения функции принадлежности по данным, представляющим функциональную зависимость между петрофизическими параметрами, с целью получения дифференцированной оценки достоверности.
Материалы и методы исследования
К петрофизическим связям, заданным аналитически, относятся такие отношения, как отношения параметров «коэффициент нефтенасыщенности», «коэффициент газонасыщенности» и параметра «коэффициент водонасыщенности».
Определение коэффициентов нефтенасыщенности и/или газонасыщенности является неотъемлемым этапом при подсчете запасов нефти и газа и проектировании разработки.
Под коэффициентом нефтенасыщенности Кн (газонасыщенности Кг) подразумевается отношение объема нефти (газа), содержащегося в открытом пустотном пространстве пород, к общему объему пустотного пространства.
Коэффициент нефтенасыщенности (газонасыщенности) не может быть определен путем исследования образцов керна, так как при выбуривании породы из образца вытесняется часть нефти (газа), а также в результате понижения давления (от пластового к атмосферному) при подъеме образца объем нефти (газа) увеличивается и часть выходит из образца, к тому же при понижении давления из нефти отделяется растворенный газ, из-за которого также из образца выходит часть нефти.
В отличие от коэффициентов нефтенасыщенности и газонасыщенности коэффициент водонасыщенности меньше зависит от внешних факторов, что позволяет с достаточной точностью рассчитывать значения данного коэффициента. Учитывая данные обстоятельства, значение коэффициента нефтенасыщенности (газонасыщенности) принято рассчитывать через определение коэффициента водонасыщенности.
Под коэффициентом водонасыщенности Кв подразумевается отношение объема воды, содержащейся в открытом пустотном пространстве пород, к суммарному объему пустотного пространства.
Коэффициенты нефтенасыщенности и газонасыщенности зависят от коэффициента водонасыщенности следующим образом:
в нефтенасыщенном коллекторе
Кн = 1 – Кв;
в газонасыщенном коллекторе
Кг = 1 – Кв;
в нефтегазонасыщенном коллекторе
Кн + Кг = 1 – Кв.
Иногда данные коэффициенты выражают в процентах [6].
Функция принадлежности μ(x, y) описывает нечеткое отношение между параметрами x и y и является оценкой достоверности одновременного появления двух (четких) значений (x, y) [7]. Данная функция принадлежности строится как выражение реальных экспериментальных данных измерения пар значений (xi, yi).
Надграфиком будем называть функцию принадлежности для отношения параметров, зависимость между которыми задана функционально.
Конструирование функции принадлежности может выполняться на базе различных моделей. В статье построение надграфиков функциональных зависимостей выполняется по двум моделям:
1. Экспоненциальная модель:
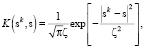
где ζ – эффективный параметр рассеяния.
2.
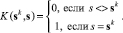
Назовем данную модель импульсной.
K(sk, s) – элемент аппроксимации, на базе которого выполняется конструирование функции принадлежности, s – сетка, на которой выполняется построение функции принадлежности, sk – координаты расположения источников исходных данных. Более подробно формирование функций принадлежности описано в статье [5].
Рассмотрим результаты построения надграфиков функциональных зависимостей по двум моделям и их влияние на результат прогноза петрофизических параметров. В качестве исходных данных были использованы одновременно измеренные значения параметров пористости по керну и остаточной водонасыщенности (рис. 1, а) и функциональная зависимость нефтенасыщенности от водонасыщенности (Кн = 1 – Ков).
Прогноз петрофизических параметров выполняется по правилам логического вывода Мамдани (композиции) нечетких отношений. В данном случае взаимосвязь между параметрами «нефтенасыщенность» и «пористость по керну» была рассчитана по формуле
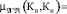
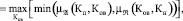
где Кп, Ков, Кн – коэффициенты пористости, остаточной водонасыщенности и нефтенасыщенности соответственно,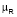 
(Ков, Кн) – надграфик функциональной зависимости нефтенасыщенности от водонасыщенности.
Принципы нечеткого логического вывода развиты в [8], а основы теории нечетких множеств изложены в [9].
Результаты исследования и их обсуждение
Результат построения функции принадлежности нечеткого отношения «пористость по керну – остаточная водонасыщенность» по экспоненциальной модели при ζ = 1,25 представлен на рис. 1, б.
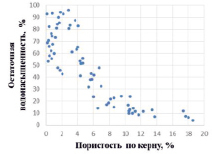
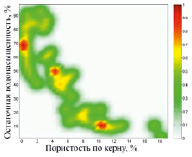
а) б)
Рис. 1. Исходные данные (одновременно измеренные значения параметров пористости по керну и остаточной водонасыщенности) (а); функция принадлежности нечеткого отношения «пористость по керну – остаточная водонасыщенность» (б)
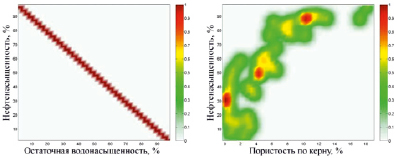
а) б)
Рис. 2. Надграфик функциональной зависимости «остаточная водонасыщенность – нефтенасыщенность», построенный по экспоненциальной модели при ζ = 0,01 (а); функция принадлежности нечеткого отношения «пористость по керну – нефтенасыщенность», полученная в результате композиции (б)
Надграфик функциональной зависимости параметра «нефтенасыщенность» от параметра «остаточная водонасыщенность», построенной по экспоненциальной модели при значении эффективного параметра 0,01, и результат композиции данного надграфика и нечеткого отношения «пористость по керну – остаточная водонасыщенность» представлены на рис. 2.
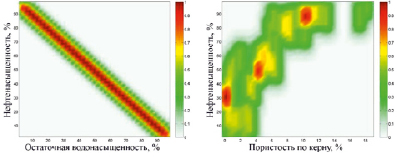
Надграфик функциональной зависимости параметра «нефтенасыщенность» от параметра «остаточная водонасыщенность», построенной по экспоненциальной модели при значении эффективного параметра 1,5, и результат композиции данного надграфика и нечеткого отношения «пористость по керну – остаточная водонасыщенность» представлены на рис. 3.
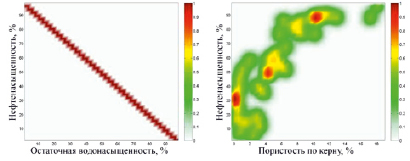
Надграфик функциональной зависимости параметра «нефтенасыщенность» от параметра «остаточная водонасыщенность», построенной по импульсной модели, и результат композиции данного надграфика и нечеткого отношения «пористость по керну – остаточная водонасыщенность» представлены на рис. 4.
а) б)
Рис. 3. Надграфик функциональной зависимости «остаточная водонасыщенность – нефтенасыщенность», построенный по экспоненциальной модели при ζ = 1,5 (а); функция принадлежности нечеткого отношения «пористость по керну – нефтенасыщенность», полученная в результате композиции (б)
а) б)
Рис. 4. Надграфик функциональной зависимости «остаточная водонасыщенность – нефтенасыщенность», построенный по импульсной модели (а); функция принадлежности нечеткого отношения «пористость по керну – нефтенасыщенность», полученная в результате композиции (б)
а) б)
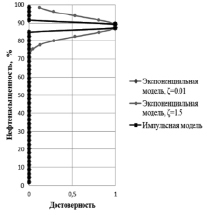
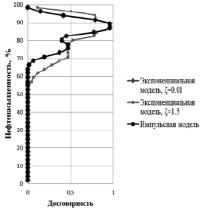
Рис. 5. Срез надграфиков функциональных зависимостей «остаточная водонасыщенность – нефтенасыщенность» при значении параметра «остаточная водонасыщенность» равном 12 (а); срез функции принадлежности нечеткого отношения «пористость по керну – нефтенасыщенность» при значении параметра «пористость по керну» равном 10 (б). Легенда на диаграммах указывает параметры моделирования, при которых были получены данные результаты
Для более наглядного представления рассмотрим срез надграфиков функциональных зависимостей и функций принадлежности, полученных в результате композиции нечетких отношений «пористость по керну – остаточная водонасыщенность» и надграфиков функциональных зависимостей «остаточная водонасыщенность – нефтенасыщенность». На рис. 5, а, представлен срез надграфиков функциональных зависимостей «остаточная водонасыщенность – нефтенасыщенность» при значении параметра «остаточная водонасыщенность» равном 12. Первым в легенде графика указан срез надграфика, построенный по экспоненциальной модели при ζ = 0,01, вторым – срез надграфика, построенный по экспоненциальной модели при ζ = 1,5, третьим – срез надграфика, построенный по импульсной модели. На рис. 5, б, представлен срез функции принадлежности нечеткого отношения «пористость по керну – нефтенасыщенность» при значении параметра «пористость по керну» равном 10. Первым в легенде графика указан срез функции принадлежности нечеткого отношения, полученной при композиции с надграфиком, построенным по экспоненциальной модели при ζ = 0,01, вторым – срез функции принадлежности нечеткого отношения, полученной при композиции с надграфиком, построенным по экспоненциальной модели при ζ = 1,5, третьим – срез функции принадлежности нечеткого отношения, полученной при композиции с надграфиком, построенным по импульсной модели.
Заключение
Результаты композиции с надграфиком функциональной зависимости показывают, что использование экспоненциальной модели при значительном эффективном параметре для функциональных зависимостей приводит к возрастанию диффузии, таким образом возрастает и мера нечеткости данных. Чтобы избежать данного эффекта, для построения надграфиков стоит использовать экспоненциальную модель при небольшом значении эффективного параметра либо импульсную модель.
Библиографическая ссылка
Кожевникова П.В., Дорогобед А.Н., Кунцев В.Е. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НАДГРАФИКОВ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ // Современные наукоемкие технологии. – 2020. – № 7. – С. 62-67;URL: https://top-technologies.ru/ru/article/view?id=38135 (дата обращения: 21.11.2024).