Интуиция, в рамках философского учения, формулируется нестрогим, неаналитическим путем, но в то же время при непосредственном усмотрении знаний, их постижимости. Знание, получаемое таким образом, т.е. без строгого обоснования, без логических доказательств, с помощью интуитивных предчувствий, интуитивности, может становиться теперь осознанным, обоснованным умственной деятельностью.
С другой стороны, в рамках обработки интеллектуальной информации, рассматривая процесс интуитивной догадки, сталкиваемся с противоречием непосредственности постижения истин, информации, так как ему предшествует значительная работа, и именно интеллектуальная работа по обработке получаемой информации. Сам интуитивный процесс восприятия и осознания обладает несколькими основными чертами, а именно: предложением альтернативы воздействий, высказыванием гипотез, оценкой результата в ходе протекания ситуации, возможности предвидения развития ситуации или ее последствий, после принятия решения [1].
Математическое образование и, в частности, геометрическое, бесспорно, играет значимую роль в становлении мышления и познания человеком окружающей действительности. Об этом напрямую высказывается И.Ф. Шарыгин: «Геометрия может и должна стать предметом, с помощью которого мы можем сбалансировать работу головного мозга, улучшить функциональное взаимодействие между полушариями. Геометрия – витамин для мозга» [2].
Можно выделить несколько компонентов математических способностей:
– быстроту мысли;
– остроумие;
– сильную память.
Таким образом, скорость протекания неосознанного мышления гораздо выше, чем у мышления сознательного.
Цель исследования: представить интуитивный компонент геометрической подготовки учащихся в виде интерпретирующей модели и охарактеризовать входящие в ее состав компоненты.
Материалы и методы исследования
Всё развитие математического творчества тесно связано в науке с понятием интуитивности. Интуитивность, ее элементы присутствуют в каждом, пусть самом незначительном по времени, но весьма важном по сути математическом рассуждении, не говоря уже об открытии. Исследователь в области научных математических дисциплин в начале своего пути формулирует мысль, сгенерированную им в процессе интуитивной работы своего мозга, а далее происходит ее обоснование, подтверждение с помощью строгих математических доводов с использованием символьных обозначений.
В математическом исследовании, в широком понимании этого процесса, крайне неоднозначно то место, которое занимает интуиция, интуитивность, интуитивное мышление, но все сходятся во мнении, что она сильно влияет на самого исследователя, математика, его характер, стиль мышления, а также особенности его деятельности. От этого напрямую зависит и его выбор подходов для решения поставленных задач. В этом случае можно утверждать о формировании стиля мышления, математического с интуитивной составляющей, которая обязательно входит в перечень системообразующих данного процесса. И уже в ходе этого мыслительного процесса наступает момент «озарения», он может возникнуть неожиданно, в результате свершается открытие, но нужно обязательно отметить, что этому «озарению» предшествовало довольно продолжительное обдумывание поставленной задачи, проблемы [3, 4].
Образным представлением творческого математического процесса мышления, зачастую в большей своей части являющегося неосознаваемым, может служить распутывание клубка из переплетений умозаключений, с помощью выстраивания логически правильных и выверенных рассуждений, в ясную и структурированную форму доказательности. То, что деятельность интуиции скрыта в подсознании, обуславливает всю сложность протекания этого процесса, крайне тяжело переформатируются полученные в ходе интуитивного умозаключения выводы и способы решения, потому что осознаваемым оказывается только ее результат.
Во время всего процесса мышления, мышления творческого, математического, происходит преобразование, логическое выстраивание всех ранее неосознаваемых образов. А затем подобное претерпевают и дискурсивные рассуждения, и уже совместно всё это формирует явное знание, которое и вербализуется. После чего это полученное знание формализуется символьно, в математических формулах и терминах.
М. Бунге систематизировал первоначальные представления о самом понятии интуитивности, интуитивном процессе восприятия, скорости протекания данного процесса, что явно выделяет его на фоне других, но в то же время не теряется чёткое понимание сути самого процесса. Также М. Бунге описывает интуитивность с точки зрения воображения, способности достраивать элементы в своем сознании. Далее им приводится, как один из важнейших компонентов, изобретательность, генерирование новых идей, способность созидания нового, в широком смысле. В завершение приводятся стадии интуиции, такие как интуитивные разум и оценка. Это, несомненно, является вершиной данных суждений, так как стремительный скачок в процессе размышления над проблемой или задачей, от одной линии рассуждений к другой, третьей, а в дальнейшем и умение оценить вклад той или иной составляющих в общий процесс решения требуют максимальных умственных усилий.
Рассмотрение интуитивности мышления в психологии всегда наталкивалось на недоверие и неприятие данного процесса умственной деятельности. Интуитивность сопоставлялась с чем-то мистическим и необъяснимым и зачастую не приводившим к верному решению.
Мы придерживаемся мнения многих философов о разбиении понятия интуитивного мышления на три ветви, а именно интуитивности чувственной, интеллектуальной и инсайту.
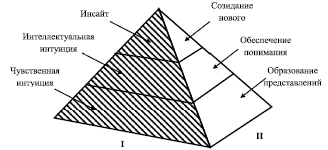
Рис. 1. Структура I и II граней интерпретирующей модели интуитивного компонента
Это послужило толчком к проработке данного вопроса и разработке интерпретирующей модели, с указанием видов интуиции и их занимаемых в этой модели мест. Структурно данная интерпретирующая модель представляет собой пирамиду с четырьмя боковыми гранями, каждой грани была присвоена определяющая ее направленность, что повлекло за собой соответствующее структурированное заполнение данной грани. Также каждая грань разбита горизонтально на три сегмента, которым в рамках уже обозначенной выше направленности придаются уровни сформированной этой самой направленности.
Так, первая грань получила название философской, а составляющие ее сегменты, по мере приближения к вершине, что соответствует повышению уровня и увеличению степени значимости, в рамках данного исследования были названы соответственно чувственной интуицией, интеллектуальной интуицией и инсайтом, что представлено на рис. 1 (I грань).
К сожалению, нет полного единения в разъяснении самого определения сути интуитивности, как термина и как заключенного в него понимания об интуитивном процессе мышления. Но большинство исследователей в данном вопросе сходятся на противопоставлении такому процессу строго логического и аналитического типов мышления. Также интуитивности приписываются креативная и творческая сущности в процессе мышления [1, 5].
Важным моментом интуитивного мышления, заслуживающим особого рассмотрения, является затратность умственных ресурсов в его использовании, так как при прекращении, пусть временном, сознательного обдумывания проблемы и поиска ее решения этот процесс не останавливается, а переходит на неосознанный «уровень», поиск решения продолжается, но уже несознательно. Итогом будет служить найденный путь решения поставленной задачи или проблемы [2, 6].
Ещё одним немаловажным фактором интуитивного мышления, безусловно, является, «предвосхищение», чувство скорого обнаружения способа решения, приближения к моменту нахождения верного ответа или способа решения поставленной задачи, что базируется на всём накопленном до этого момента опыте в данном вопросе.
Образное мышление, в рамках данного исследования, соотносится с интуитивностью чувственной, оперирующей образами уже воспринимавшимися ранее в человеческом сознании. Само же выявление из множества представленных вариантов истинного, верного решения будет соотноситься с интуитивностью, уже интеллектуальной. Высшая же стадия интеллектуальной интуитивности – инсайт – будет тождественна открытиям, сделанным учеными и изобретателями.
Всё вышеизложенное послужило основой формирования второй грани предлагаемой интерпретирующей модели, отвечающей уже за психологическую составляющую, которая, в соответствии с уже установленным для первой грани порядком, имеет такие же три сегмента, обозначенные как «образование представлений», «обеспечение понимания» и самого важного, стоящего на вершине этой грани – «созидание нового» представлено (рис. 1 (II грань)).
При дальнейшем рассмотрении компонентов, входящих в описываемую интерпретирующую модель интуитивного компонента геометрической подготовки учащихся, необходимо обратиться к самой теории и методике обучения математике и, как её составляющей, теории и методике обучения геометрии. Проделанный анализ позволил наполнить интерпретирующую модель интуитивного компонента геометрическими терминами, понятиями, категориями, участвующими в самом процессе обучения геометрии. Что легло в основу третьей грани предлагаемой интерпретирующей модели интуитивного компонента, призванной отвечать за содержание математической деятельности, а именно геометрическую его составляющую, согласно предлагаемой модели три, соответствующих элемента, а именно – геометрические закономерности, геометрические зависимости и геометрические представления, что и видно на рис. 2 (III грань).
Простейшие знания о геометрических фигурах могут складываться в процессе разбора заданий вариативно-позиционной направленности. Выполнение же заданий ситуационно-динамического плана призвано усилить формирование представлений о геометрических зависимостях. И, наконец, на вершине этой четвертой грани, которую в интерпретирующей модели занимает методико-инструментальная грань, располагаются динамико-эвристические задания, способствующие формированию представлений о геометрических закономерностях (свойствах), что нашло отражение на рис. 2 (IV грань).
Представленная структура интуитивного компонента геометрической подготовки учащихся в виде интерпретирующей модели (пирамиды) наглядно демонстрирует все уровни связей, как в рамках одной грани, так и сегментов одного уровня в соседних гранях. Множество этих взаимосвязей между сегментами интерпретирующей модели (пирамиды) описывают мыслительные переходы одних образных представлений к другим, а также взаимопереходы между логическими умозаключениями. Но особую ценность представляют переходы от наглядных образов к логическим умозаключениям. В этом и есть сущность самого формирования описанного выше интуитивного компонента и представленной интерпретирующей его модели. Что является важным для дальнейшего использования в процессе обучения как геометрии, так и всем математическим и смежным с ними дисциплинам.
Результаты исследования и их обсуждение
В качестве результатов может быть использована приведенная на рис. 3 структура интуитивного компонента геометрической подготовки учащихся, со всеми входящими в ее состав элементами.
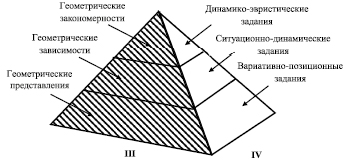
Рис. 2. Структура III и IV граней интерпретирующей модели
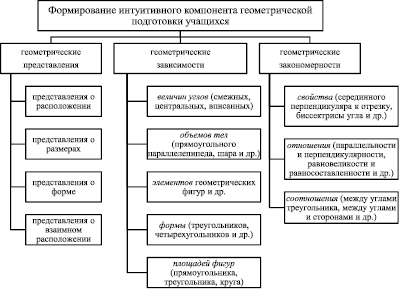
Рис. 3. Содержательные элементы интуитивного компонента геометрической подготовки учащихся
Заключение
В статье приведен системный анализ представлений о сущности и роли интуитивности, используемой в процессе освоения новых знаний. Также охарактеризованы основные виды интуиции: чувственная, интеллектуальная, инсайт. Представлена интерпретирующая модель интуитивного компонента геометрической подготовки учащихся, даны характеристики каждой из составляющих предложенной интерпретирующей модели. Описаны взаимосвязи между элементами интерпретирующей модели интуитивного компонента геометрической подготовки учащихся, уровни связей как в рамках одной грани, так и сегментов одного уровня в соседних гранях. Также данная модель описывает мыслительные переходы одних образных представлений к другим, а также взаимопереходы между логическими умозаключениями. Но особую ценность представляют переходы от наглядных образов к логическим умозаключениям. Далее приведены содержательные элементы интуитивного компонента геометрической подготовки учащихся, с помощью которых можно обновлять объём практических заданий для решения в процессе обучения математическим дисциплинам.
Библиографическая ссылка
Курдин Д.А., Фролов И.В. СОДЕРЖАТЕЛЬНЫЕ ЭЛЕМЕНТЫ ИНТЕРПРЕТИРУЮЩЕЙ МОДЕЛИ ИНТУИТИВНОГО КОМПОНЕНТА ГЕОМЕТРИЧЕСКОЙ ПОДГОТОВКИ УЧАЩИХСЯ // Современные наукоемкие технологии. 2020. № 6-2. С. 348-352;URL: https://top-technologies.ru/ru/article/view?id=38114 (дата обращения: 01.01.2026).
DOI: https://doi.org/10.17513/snt.38114



