Излагаемая работа является непосредственным продолжением работы [1]. В [1] представлены основные понятия, определения, принципы подхода, конструкции алгоритмов и примеры программ. Ниже эта информация не дублируется. Метод из [1] позволяет по инвариантной программе находить нули и экстремумы различных функций, в том числе корни полиномов от одной действительной переменной в произвольно заданной области. При этом границы поиска задаются произвольно, начальные положения нулей и экстремумов не указываются, программа автоматически идентифицирует одновременно все нули и локальные экстремумы с произвольным априори заданным радиусом локализации. Ниже данный метод переносится на случай функции двух действительных переменных. Поиск нулей функции комплексной переменной сводится к этому случаю путем умножения функции на комплексно сопряженное значение. В частности, так находятся корни полиномов от одной комплексной переменной с комплексными коэффициентами. Предложенная программная реализация в своей основе сохраняет инвариантность во всех рассматриваемых применениях с точностью до специфики задания входных функций и полиномов. В частности, программа находит все корни характеристического полинома матрицы с учетом кратности, результаты интерпретируются в аспекте анализа устойчивости линейной системы обыкновенных дифференциальных уравнений (ОДУ) с данной матрицей коэффициентов. Программа строится на основе сортировки, все вычислительные операции заменяются операциями сравнения, в результате достигается точность приближения нулей и экстремумов без потери значащих цифр в формате представления данных. Рассматриваемые вопросы актуальны [2, 3], практически значимы, метод позволяет обойти вычислительную неустойчивость решения данных задач, представляющую собой одну из основных трудностей [4, 5] их решения. В аспекте анализа устойчивости систем линейных ОДУ результаты применения метода отличаются [6] инвариантностью относительно вида матрицы коэффициентов. В целом от известных методов поиска нулей и экстремумов предложенный способ отличается [7, 8] по своему построению, свойствами вычислительной устойчивости и минимизации погрешности, включая случай, когда экстремумы априори не локализованы. Метод преобразуется к максимально параллельной форме, даны соответствующие оценки временной сложности. Конкретно в работе ставится задача построить на основе сортировки метод безусловной численной оптимизации и одновременно решения задач вычислительной линейной алгебры, инвариантный относительно задачи с точностью до вида входной функции, программно реализовать метод, раскрыть его качество минимизации погрешности и на основе численного эксперимента указать систему ограничений.
В работе ставится цель исследовать и обосновать возможность построения инвариантного метода компьютерной идентификации нулей и экстремумов функций двух действительных и одной комплексной переменных на основе устойчивой адресной сортировки. Инвариантность относится к виду входной функции, к области поиска одновременно всех нулей и экстремумов без их априорной локализации. Требуется представить единую программную реализацию метода, исключив элементы эвристичности (что не достигалось в прототипе [9]), провести численный эксперимент в основных аспектах применения, который иллюстрировал бы свойства вычислительной устойчивости и минимизации погрешности. Требуется показать реализуемость метода с приемлемыми оценками времени на персональном компьютере и указать преобразование к параллельной форме с оценками временной сложности. Исследование акцентируется на свойстве метода выполнять численную оптимизацию без априорного указания области нулей и экстремумов, структуры их расположения, без локализации начальных приближений, дополнено аналитическими оценками области корней полиномов и характеристических чисел матрицы.
Идентификация комплексных корней полинома с комплексными коэффициентами в прямоугольной области
Изложенный в [1] метод распространяется на идентификацию комплексных корней полинома с комплексными коэффициентами с помощью перехода к модулю полинома как функции двух действительных переменных. После выполнения перехода последовательно используется первоначальный [1] способ по каждой действительной переменной по отдельности. При этом имеют место следующие особенности. Полином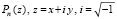 
преобразуется в неотрицательную действительную функцию двух действительных переменных посредством умножения на комплексно сопряженное значение. Полученная функция 
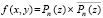поступает на вход метода. Согласно следствию принципа минимума точками минимумов этой функции на декартовой плоскости могут быть ее нули (корни полинома Pn(z)) и только они [10]. При этом ноль, идентифицированный по одной переменной, означает, что ему однозначно соответствует ноль по второй переменной, соответственная пара нулей дает действительную и мнимую часть корня полинома. Пусть требуется выполнить идентификацию корней в квадратной (прямоугольной) области. Вся область покрывается равномерной квадратной (прямоугольной) сеткой со сторонами квадрата длины H (прямоугольника 
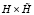). В программной реализации длина H будет обозначаться hh. Каждый горизонтальный слой сетки обходится слева направо аналогично тому, как описано для функции одной переменной [1], однако при фиксированном значении другой переменной. Последовательность всех горизонтальных слоев обходится сверху вниз. Каждый квадрат H×H в свою очередь покрывается мелкой квадратной сеткой со стороной квадрата h. При обходе горизонтального слоя квадрата H×H выполняется идентификация каждого минимума по текущей переменной аналогично идентификации минимума функции одной действительной переменной. Как и в случае одной переменной, выбор h определяет длину стороны квадрата H(hh) – с учетом числа nn0 элементов сортируемого массива: hh:=nn0*h; Радиус локализации [1] eps0 должен быть меньше половины расстояния между проекциями по крайней мере на одну из осей координат ближайших друг к другу корней. Согласно численному эксперименту шаг h должен быть меньше eps0/40, например h=eps0/43. Особенная часть этого процесса состоит в том, что вначале в качестве текущего элемента сортируемого массива берется наименьшее по всем элементам сетки с шагом h внутри квадрата H×H значение при фиксированной ординате 
:
{формирование входного массива для сортировки}
for r:=1 to nn0 do begin x:=x0+r*h;
ykk0:=y0; y:=y0; tty:=n00; hy:=h; miny (x,y,min,ee1); a1[r]:=min end;
После этого среди элементов сформированного массива идентифицируется локальный минимум:
{идентификация локального минимума по переменной x}
sort( nn0, a1, e3); k:=1; while k<= nn0 do begin for r := 1 to k-1 do
if abs(e3[k]-e3[k-r]) <=eps0/h then goto 23; xk:= x0+e3[k]*h; …
Другая особенность состоит в том, что, как только сформирован (в данном дискретном приближении) локальный минимум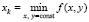 
, он фиксируется, и непосредственно при этом значении абсциссы, теперь уже в полной аналогии случаю одной действительной переменной, на данной равномерной сетке с шагом h изложенным в [1] способом (в рассматриваемом приближении) идентифицируется минимум по другой переменной 
:
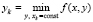{идентификация локального минимума по переменной y}
k1:=1; while k1<= nn0 do begin for r := 1 to k1-1 do
if abs(e33[k1]-e33[k1-r])<=eps0/h then goto 22; yk:= y0+e33[k1]*h; …
При фиксированном xk процесс рекуррентно продолжает поиск yk по всем квадратам H×H соответственного вертикального слоя. Приближение точки минимума определяют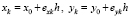 
. Здесь exk, eyk – входные индексы элементов, запомненные на выходе сортировки (устойчивая адресная сортировка слиянием, использованная в [1]), x0 и y0 – начальные координаты на границах текущего квадрата H×H. Приближение (xk, yk) уточняется путем описанного для случая одной переменной спуска [1], причем по каждой переменной отдельно, и с чередованием выполняется двукратное повторение такого спуска. Данный процесс рекуррентно продолжает поиск xk+1 при фиксированном yk, затем (xk+1, yk+1), и т.д. В текущем квадрате H×H процесс заканчивается после идентификации всех корней c находящимися в нем их мнимыми частями, соответственными проверяемой действительной части. При достижении границ квадрата выполняется переход к следующему сверху вниз квадрату. На границах выполняется проверка идентифицированного наименьшего значения на локальную минимальность по аналогии со случаем функции одной переменной [1]. После окончания прохода по одному вертикальному слою выполняется переход к следующей локализованной действительной части верхнего квадрата с новым соответственным проходом по всему вертикальному слою. После исчерпания идентифицированных в квадрате действительных частей с соответственными им мнимыми частями во всем вертикальном слое совершается переход к следующему квадрату горизонтального слоя. После каждого перехода от одного квадрата к другому полностью воспроизводятся действия по изложенной схеме. После исчерпания квадратов верхнего слоя области выполняется переход к следующему сверху вниз горизонтальному слою с полным анализом соответственного полного вертикального слоя. Процесс продолжается до обхода всей априори заданной области.
Пример 1. Пусть требуется идентифицировать корни полинома 18-й степени в квадрате 16×16 с центром в начале декартовых координат на комплексной плоскости. Для проверки правильности программы корни задаются в разделе констант этой программы. Отдельно задается массив действительных частей корней a[i] (в программе b[i]) и в соответственной последовательности – массив мнимых частей b[i] (в программе b1[i]). Комплексный корень определяется действительной и мнимой частью с равными индексами: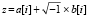 
. Полиномы восстанавливаются из двух данных массивов подпрограммой-функцией func (x,y). В приводимой ниже программе и в других программах, предназначенных для экспериментальной проверки метода, квадрат модуля полинома задается по формуле, составленной из значений действительных и мнимых частей корней [9]:
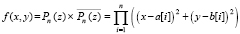. (1)
PROGRAM korkompmin;
{$APPTYPE CONSOLE}
uses
SysUtils;
label 21,22,23;
{параметры: граница погрешности, радиус локализации, шаг, число сортируемых элементов}
const eps=1.1e-44; eps0=0.049; h=eps0/43; n00=1024;
{область поиска} x00=-8; x11=8; y00=-8; y11=8; mm=4; np1=18;
type vect1=array [1..4*n00] of extended; vect2=array [1..4*n00] of longint;
vect3=array [1..np1] of extended;
const
b: vect3 =
(-2.1,-2,-1,0.102,0.203,0.302,0.401,0.505,0.602,0.701,0.805,1.5,1.6,2,6,6.1,7,7.1);
b1: vect3 =
(2.1,2,-1,0.107,0.203,0.309,0.404,0.503,0.603,0.702,0.806,1.5,1.6,-2,4,5,6,7);
var i,j,k,k1,r,ee,ee1,tty,nn0: longint; c,a1: vect1; e,e3, e33: vect2;
aaa, x,x0,xk,xk0,xk1,hx,hy,min,eps1,eps11,eps12,eps13,z,z1: extended;
bbb, y,y0,yk,yk0,yk1,ykk0,hh,yz,yz1: extended;
{задание квадрата модуля полинома степени np1}
function func (x,y:extended):extended;
var p: extended; i1: integer;
begin
p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func:=abs(p);
{func:=abs(Ln(1+abs(p)));}
{func:=exp(sin(x*y))-exp(-1)-9;}
end;
{процедуры выбора наименьшего значения}
procedure minx (var x,y,min:extended;var ee:integer);
begin min:=func(x,y); ee:=0; for i:=1 to mm do begin x:=xk0+i*hx;
if min > func(x,y) then begin min:=func(x,y); ee:=i end end end;
procedure miny (var x,y,min:extended;var ee1:integer);
begin min:=func(x,y); ee1:=0; for i:=1 to tty do begin y:=ykk0+i*hy;
if min > func(x,y) then begin min:=func(x,y);ee1:=i end end end;
{процедура сортировки слиянием}
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
type vecc=array[0..4*n00] of longint;
var ab: integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;
begin
p:= trunc(ln(nn0)/ln(2)); if p <> ln(nn0)/ln(2) then p := p+1;
n:= round(exp(p*ln(2)));
for l := 1 to n do if l<=nn0 then e[l] := l else ab:=1;
for r := 1 to p do begin m :=round(exp(r*ln(2))); nm:=n div m;
for k := 0 to nm-1 do begin
for l := 1 to m div 2 do begin
if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab := l
else e1[l] := e[k * m + l];
if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab := 1
else e2[l] := e[k * m + m div 2 + l] end;
i := 1; j := 0;
while i + j <= m do begin
if i = m div 2 + 1 then ab := -1;
if j = m div 2 then ab := 1 ;
if (k * m + i > nn0) or (e[k * m + i]>nn0)
or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)
then ab:=1;
if (i <= m div 2) and (j <= m div 2 -1) and (k * m + i<= nn0)
and (k * m + m div 2 + j <= nn0-1)
then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab := 1 else
begin if c[e2[j + 1]] - c[e1[i]]= 0 then ab := 0;
if c[e2[j + 1]] - c[e1[i]]> 0 then ab := 1;
if c[e2[j + 1]] - c[e1[i]]< 0 then ab := -1
end; if ab >= 0 then
begin e[k * m + i + j] := e1[i]; i := i + 1 end
else begin e[k * m + i + j] := e2[j + 1]; j := j + 1 end
end end end end;
{процедуры спуска для уточнения корня}
procedure spuskx( var eps1, xk0,xk1,hx,y: extended);
begin while abs(eps1) > eps do begin x:=xk0; minx (x,y,min,ee); eps1:=eps1/1.2;
xk0:=xk0+ee*hx-eps1;xk1:=xk0+eps1;hx:=abs(2*eps1)/mm end end;
procedure spusky(var eps11,yk0,yk1,hy,x: extended);
begin while abs(eps11) > eps do begin ykk0:=yk0; y:=yk0; tty:=mm;
miny (x,y,min,ee1); eps11:=eps11/1.2; yk0:=yk0+ee1*hy-eps11; yk1:=yk0+eps11;
hy:=abs(2*eps11)/mm end end;
{раздел инструкций}
begin
aaa:=1e62; bbb:=1e62; x0:=x00; y0:=y00; nn0:=n00; hh:=nn0*h;
while x0 <= x11+hh do begin
while y0 <= y11+hh do begin
{формирование входного массива для сортировки}
for r:=1 to nn0 do begin x:=x0+r*h;
ykk0:=y0; y:=y0; tty:=n00;hy:=h; miny (x,y,min,ee1); a1[r]:=min end;
sort( nn0, a1, e3);
{идентификация локального минимума по переменной x}
k:=1; while k<= nn0 do begin
for r := 1 to k-1 do if abs(e3[k]-e3[k-r]) <=eps0/h then goto 23; xk:= x0+e3[k]*h;
for r:=1 to nn0 do begin y:=y0+r*h; a1[r]:=func(xk,y) end;
sort( nn0, a1, e33);
{идентификация локального минимума по переменной y}
k1:=1; while k1<= nn0 do
begin for r := 1 to k1-1 do if abs(e33[k1]-e33[k1-r])<=eps0/h then goto 22; yk:= y0+e33[k1]*h;
eps1:=eps0; eps11:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; hx:=abs(2*eps1)/mm; y:=yk;
spuskx(eps1,xk0,xk1,hx,y);
yk0:=yk-eps11; yk1:=yk+eps11; hy:=abs(2*eps11)/mm; x:=xk0+ee*hx+eps1;
spusky( eps11,yk0,yk1,hy,x); eps12:=eps0/2;
xk0:=x-eps12; xk1:=x+eps12; hx:=abs(2*eps12)/mm; y:=yk0+ee1*hy+eps11;
spuskx( eps12, xk0,xk1,hx,y); eps13:=eps0/2;
yk0:=yk0+ee1*hy-eps13; yk1:=yk0+2*eps13; hy:=abs(2*eps13)/mm; x:=xk0+ee*hx+eps12;
spusky( eps13,yk0,yk1,hy,x);
if func(xk,yk)= 0 then begin x:=xk; yk0:=yk; goto 21 end;
{склеивание границ текущих квадратов}
for i:= 1 to 2 do begin z:=x+i*h; if func(x,yk0) >= func(z,yk0) then goto 23; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x,yk0) >= func(z1,yk0) then goto 23; end;
for i:= 1 to 2 do begin yz:=yk0+i*h; if func(x,yk0) >= func(x,yz) then goto 22; end;
for i:= 1 to 2 do begin yz1:=yk0-i*h; if func(x,yk0) >= func(x,yz1) then goto 22; end;
if abs(aaa-x)<=1e-50 then goto 23; if abs(bbb-yk0)<=1e-50 then goto 22;
21: if func(x,yk0)<=1e-30 then begin
writeln (' ', x:30,' '); writeln (' ', yk0:30,' ', func(x,yk0)); writeln; aaa:=x; bbb:=yk0;
end;
22: k1:=k1+1 end;
23: k:=k+1 end;
{циклическое прохождение области поиска}
y0:=y0+hh end; x0:=x0+hh; y0:=y00 end;
readln;
end.
В данной программе операторы if func(x,yk0)<=1e-30 then … используются, чтобы исключить вывод менее точных приближений искомых корней. Операторы if abs(aaa-x)<=1e-50 then goto 23; if abs(bbb-yk0)<=1e-50 then goto 22; исключают последовательный повтор выводимых значений. Эти операторы, используемые для наглядности выводимых значений, могут «фильтровывать» искомые корни, в общем случае желательно ими не пользоваться (но тогда будет выводиться много лишних и повторяющихся приближений). Результат работы программы:
-1.00000000000000000E+0000 -2.00000000000000000E+0000
2.00000000000000000E+0000 0.0000….0000 -1.00000000000000000E+0000 0.0000…0000
-2.10000000000000000E+0000 1.02000000000000000E-0001
2.10000000000000000E+0000 0.0000…0000 1.07000000000000000E-0001 0.0000…0000
4.01000000000000000E-0001 5.05000000000000000E-0001
4.04000000000000000E-0001 0.0000…0000 5.03000000000000000E-0001 0.0000…0000
6.02000000000000000E-0001 3.02000000000000000E-0001
6.03000000000000000E-0001 0.0000…0000 3.09000000000000000E-0001 0.0000…0000
7.01000000000000000E-0001 2.03000000000000000E-0001
7.02000000000000000E-0001 0.0000…0000 2.03000000000000000E-0001 0.0000…0000
8.05000000000000000E-0001 2.00000000000000000E+0000
8.06000000000000000E-0001 0.0000…0000 -2.00000000000000000E+0000 0.0000…0000
1.50000000000000000E+0000 1.60000000000000000E+0000
1.50000000000000000E+0000 0.0000…0000 1.60000000000000000E+0000 0.0000…0000
6.00000000000000000E+0000 6.10000000000000000E+0000
4.00000000000000000E+0000 0.0000…0000 5.00000000000000000E+0000 0.0000…0000
7.00000000000000000E+0000 7.10000000000000000E+0000
6.00000000000000000E+0000 0.0000…0000 7.00000000000000000E+0000 0.0000…0000
В левой колонке парами сверху вниз идут действительная и мнимая части комплексного корня, правой колонке – соответственное значение полинома. Таким образом, все комплексные корни полинома 18-й степени с комплексными коэффициентами идентифицированы без потери значащих цифр в формате вывода данных. При этом действительные или мнимые части некоторых корней априори взаимно отделялись на 0.1.
Идентификация области корней, структуры области и корней полинома
Если программу korkompmin примера 1 непосредственно применить к полиному с произвольным расположением корней на комплексной плоскости, то без априорной оценки эвристически заданные границы области корней могут оказаться либо избыточными, с неприемлемым замедлением работы программы, либо, напротив, узкими, что может привести к потере корней. Вместе с тем определить границы области можно из этой же программы, если априори взять заведомо избыточное начальное значение границ, при этом задать сравнительно большой радиус локализации (относительно выбора его величины сохраняются замечания, данные для случая одной действительной переменной [1]). Весь процесс поясняется на основе следующего примера.
Пример 2. Пусть требуется идентифицировать область корней, ее структуру и сами корни полинома 45-й степени. Полином задан согласно (1) значениями действительных и мнимых частей в разделе констант программы, по которым затем его модуль восстанавливается функцией func (x,y).
PROGRAM OBLASTIKORNI;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n00=1024; np1=45;
type vect1=array [1..4*n00] of extended; vect2=array [1..4*n00] of longint;
vect3=array [1..np1] of extended;
const b: vect3 =
(-4,4,0,0,0,0,0,0,-777.23, 777.23,-555.077,555.077,-111,111,-2.1,-2,
-1,0.102,0.203,0.302,0.401,0.505,0.602,0.701,0.805,1.5,1.6, 2, 77, 79.01, 8.09,19.010203,20,
-77,55.01,54.1,80.01,0.101,0.202, 8.109, 7.109, 7.109, 0, -1.000001, 0);
b1: vect3 =
(4,-4,2,-2,-5,-5.1,5,5.1,555.077,-555.077,777.23,-777.23,-111,111,2.1,2,
-1,0.107,0.203,0.309,0.404,0.503,0.603,0.702,0.806,1.5,1.6,-2,-55,-79.01, -4.03,19.0987,-20,
67,8.02,-4.11,0.906,54.101,80.202,-4.103,-4.103,-4.203,0.000001, 0, -1.000001);
var i,ii,j,k,kk,k1,r,ee,ee1,tty,nn0, mm: longint; c,a1,rex,imy: vect1; e,e3, e33: vect2;
aaa, x,x0,xk,xk0,xk1,hx,hy,min,eps1,eps11,eps12,eps13,z,z1: extended;
bbb, y,y0,yk,yk0,yk1,ykk0,hh,yz,yz1, x00, x11, y00, y11,eps0, h, eps00,eps:extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
{процедура сортировки слиянием без изменения скопирована
из программы korkompmin примера 1}
procedure identif1(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended;
var rex,imy: vect1;var kk:longint;var mm:longint);
label 21,22,23;
function func (x,y:extended):extended;
var p: extended; i1: integer;
begin
p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func:=abs(p);
end;
procedure minx (var x,y,min:extended;var ee:integer);
begin min:=func(x,y); ee:=0; for i:=1 to mm do begin x:=xk0+i*hx;
if min > func(x,y) then begin min:=func(x,y);ee:=i end end end;
procedure miny (var x,y,min:extended;var ee1:integer);
begin min:=func(x,y); ee1:=0; for i:=1 to tty do begin y:=ykk0+i*hy;
if min > func(x,y) then begin min:=func(x,y);ee1:=i end end end;
procedure spuskx( var eps1, xk0,xk1,hx,y: extended);
begin while abs(eps1) > eps do begin x:=xk0; minx (x,y,min,ee); eps1:=eps1/1.2;
xk0:=xk0+ee*hx-eps1;xk1:=xk0+eps1;hx:=abs(2*eps1)/mm end end;
procedure spusky(var eps11,yk0,yk1,hy,x: extended);
begin while abs(eps11) > eps do begin ykk0:=yk0; y:=yk0; tty:=mm;
miny (x,y,min,ee1); eps11:=eps11/1.2; yk0:=yk0+ee1*hy-eps11; yk1:=yk0+eps11;
hy:=abs(2*eps11)/mm end end;
begin
aaa:=1e62;bbb:=1e62;kk:=0; x0:=x00; y0:=y00; nn0:=n00; hh:=nn0*h;
while x0 <= x11+hh do begin while y0 <= y11+hh do begin
for r:=1 to nn0 do begin x:=x0+r*h;ykk0:=y0; y:=y0; tty:=n00;hy:=h;
miny (x,y,min,ee1); a1[r]:=min end; sort( nn0, a1, e3);
k:=1; while k<= nn0 do begin
for r := 1 to k-1 do if abs(e3[k]-e3[k-r]) <=eps0/h then goto 23; xk:= x0+e3[k]*h;
for r:=1 to nn0 do begin y:=y0+r*h; a1[r]:=func(xk,y) end; sort( nn0, a1, e33);
k1:=1; while k1<= nn0 do begin for r := 1 to k1-1 do
if abs(e33[k1]-e33[k1-r])<=eps0/h then goto 22; yk:= y0+e33[k1]*h; eps1:=eps0; eps11:=eps0;
xk0:=xk-eps1; xk1:=xk+eps1; hx:=abs(2*eps1)/mm; y:=yk; spuskx(eps1,xk0,xk1,hx,y);
yk0:=yk-eps11; yk1:=yk+eps11; hy:=abs(2*eps11)/mm; x:=xk0+ee*hx+eps1;
spusky( eps11,yk0,yk1,hy,x); eps12:=eps0/1.2; xk0:=x-eps12; xk1:=x+eps12;
hx:=abs(2*eps12)/mm; y:=yk0+ee1*hy+eps11; spuskx(eps12, xk0,xk1,hx,y); eps13:=eps0/1.2;
yk0:=yk0+ee1*hy-eps13; yk1:=yk0+2*eps13; hy:=abs(2*eps13)/mm;
x:=xk0+ee*hx+eps12; spusky( eps13,yk0,yk1,hy,x);
if func(xk,yk)= 0 then begin x:=xk; yk0:=yk; goto 21 end;
for i:= 1 to 2 do begin z:=x+i*h; if func(x,yk0) >= func(z,yk0) then goto 23; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x,yk0) >= func(z1,yk0) then goto 23; end;
for i:= 1 to 2 do begin yz:=yk0+i*h; if func(x,yk0) >= func(x,yz) then goto 22; end;
for i:= 1 to 2 do begin yz1:=yk0-i*h; if func(x,yk0) >= func(x,yz1) then goto 22; end;
if abs(aaa-x)<=1e-50 then goto 23; if abs(bbb-yk0)<=1e-50 then goto 22;
21: kk:=kk+1; rex[kk]:=x; imy[kk]:=yk0;
if func(x,yk0)<=1e-3{30} then begin writeln (' ', x:30,' ');
writeln (' ', yk0:30,' ', func(x,yk0):30); writeln; aaa:=x; bbb:=yk0; end;
22: k1:=k1+1 end;
23: k:=k+1 end; y0:=y0+hh end; x0:=x0+hh; y0:=y00 end; end;
begin
eps:=1e-44; mm:=4; x00:=-1000; x11:=1000; y00:=-1000; y11:=1000;
eps0:= 4.9; h:=eps0/43;eps00:= eps0;
writeln; writeln (' ','Приближения корней',' '); writeln;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней ',' '); writeln ;
eps0:= eps00/10; h:=eps0/43;
for ii:= 1 to kk do
begin
x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
end;
x00:=-200; x11:=200; y00:=-200; y11:=200; eps0:= 0.49; h:=eps0/43;eps00:= eps0;
writeln; writeln (' ','Приближения корней',' '); writeln ;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней',' '); writeln ;
eps0:= eps00/10; h:=eps0/43;
for ii:= 1 to kk do
begin
x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
end;
x00:=-20; x11:=20; y00:=-20; y11:=20; eps0:= 0.049; h:=eps0/43; eps00:= eps0;
writeln; writeln (' ','Приближения корней ',' '); writeln ;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней ',' '); writeln ;
eps0:= eps00/10; h:=eps0/43;
for ii:= 1 to kk do
begin
x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
end;
x00:=-2; x11:=2; y00:=-2; y11:=2; eps:=1e-144; mm:=32; eps0:= 0.0049; h:=eps0/43;eps00:= eps0;
writeln; writeln (' ','Приближения корней',' '); writeln ;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней',' '); writeln; eps0:= eps00/10;h:=eps0/43;
for ii:= 1 to kk do
begin
x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln; end.
Результат работы программы (исключены менее точные и повторяющиеся значения):
-7.77230000000000000E+0002 -5.55077000000000000E+0002
5.55077000000000000E+0002 0.0000…0000 7.77230000000000000E+0002 0.0000…0000
-7.70000000000000000E+0001 4.01000000000000000E-0001
6.70000000000000000E+0001 0.0000…0000 4.04000000000000000E-0001 0.0000…0000
-2.00000000000000000E+0000 7.10900000000000000E+0000
2.00000000000000000E+0000 0.0000…0000 -4.10300000000000000E+0000 0.0000…0000
8.09000000000000000E+0000 6.02000000000000000E-0001
-4.03000000000000000E+0000 0.0000…0000 6.03000000000000000E-0001 0.0000…0000
2.02000000000000000E-0001 7.90100000000000000E+0001
8.02020000000000000E+0001 0.0000…0000 -7.90100000000000000E+0001 0.0000…0000
5.41000000000000000E+0001 5.50100000000000000E+0001
-4.11000000000000000E+0000 0.0000…0000 8.02000000000000000E+0000 0.0000…0000
2.03000000000000000E-0001 8.00100000000000000E+0001
2.03000000000000000E-0001 0.0000…0000 9.06000000000000000E-0001 0.0000…0000
5.55077000000000000E+0002 7.77230000000000000E+0002
-7.77230000000000000E+0002 0.0000…0000 -5.55077000000000000E+0002 0.0000…0000
-1.11000000000000000E+0002 1.02000000000000000E-0001
-1.11000000000000000E+0002 0.0000…0000 1.07000000000000000E-0001 0.0000…0000
3.02000000000000000E-0001 5.05000000000000000E-0001
3.09000000000000000E-0001 0.0000…0000 5.03000000000000000E-0001 0.0000…0000
7.01000000000000000E-0001 1.50000000000000000E+0000
7.02000000000000000E-0001 0.0000…0000 1.50000000000000000E+0000 0.0000…0000
1.60000000000000000E+0000 8.05000000000000000E-0001
1.60000000000000000E+0000 0.0000…0000 8.06000000000000000E-0001 0.0000…0000
-1.00000000000000000E+0000 1.01000000000000000E-0001
-1.00000000000000000E+0000 0.0000…0000 5.41010000000000000E+0001 0.0000…0000
2.00000000000000000E+0001 7.10900000000000000E+0000
-2.00000000000000000E+0001 0.0000…0000 -4.20300000000000000E+0000 0.0000…0000
1.90102030000000000E+0001 7.70000000000000000E+0001
1.90987000000000000E+0001 0.0000…0000 -5.50000000000000000E+0001 0.0000…0000
1.11000000000000000E+0002 -4.00000000000000000E+0000
1.11000000000000000E+0002 0.0000…0000 4.00000000000000000E+0000 0.0000…0000
-2.10000000000000000E+0000 4.00000000000000000E+0000
2.10000000000000000E+0000 0.0000…0000 -4.00000000000000000E+0000 0.0000…0000
7.10900000000000000E+0000 -1.00000100000000000E+0000
-4.10300000000000000E+0000 0.0000…0000 0.00000000000000000E+0000 0.0000...0000
0.00000000000000000E+0000 0.00000000000000000E+0000
-5.00000000000000000E+0000 0.0000…0000 -5.10000000000000000E+0000 0.0000…0000
0.00000000000000000E+0000 0.00000000000000000E+0000
2.00000000000000000E+0000 0.0000…0000 5.00000000000000000E+0000 0.0000…0000
0.00000000000000000E+0000 2.00000000000000000E+0000
5.10000000000000000E+0000 0.0000…0000 -2.00000000000000000E+0000 0.0000…0000
8.75460310550294812E-0145 0.00000000000000000E+0000
1.00000000000000000E-0006 6.85390E-0203 -2.00000000000000000E+0000 0.0000…0000
0.00000000000000000E+0000
-1.00000100000000000E+0000 0.0000…0000
Найдены 45 различных комплексных корней полинома 45-й степени с комплексными коэффициентами без погрешности в формате представления данных. В числе корней те, действительные части которых взаимно отделены на 0.1, а мнимые части совпадают. У некоторых мнимые части отделены на 0.1, а действительные части равны. Представленная ранее программа korkompmin в рассматриваемом случае эквивалентно преобразована в процедуру identif1(eps, x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); В отличие от программы-прототипа, параметры процедуры, включая границы области поиска корней, границы абсолютной погрешности, радиусы локализации, количество элементов сетки спуска, определены как переменные. Это сделано для уточнения искомых корней посредством повторения процедуры на участке с переменными границами области корней. Действительные и мнимые части предварительно вычисленных корней запоминаются в качестве соответственных элементов массивов rex[kk]:=x; imy[kk]:=yk0; Их уточнение выполняется с отступами на радиус локализации, с которым эти корни были первоначально приближены: влево и вправо от действительной и мнимой части данного элемента массива. Такими отступами определяются границы, внутри которых затем выполняется поиск более точных значений (или значений, отделенных на меньшую величину). В новых границах выполняется обращение к процедуре identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0, rex,imy,kk,mm). Кроме того, обращение выполняется в цикле по всем элементам массива, при этом радиус локализации уменьшен в десять раз по сравнению с тем, который использован для нахождения первичных приближений корней. Входные границы области определялись как стороны квадрата длиной 2000 на комплексной плоскости с центром в начале координат. Следует заметить, что та же программа дала бы верные значения всех корней без изменения параметров предыдущей программы, при этом время вычисления уменьшилось бы. Однако один из корней в этом случае имел бы низкую точность приближения, именно:
2.49265564117508969E-0045
1.00000000000000000E-0006 5.55635185968440483E-0004
При рассмотрении программы OBLASTIKORNI необходимо принять во внимание, что последовательность обращений к процедуре определена с учетом структуры расположения корней. Получить предварительное представление о структуре можно посредством одного (или двух-трех с сокращением вдвое радиуса локализации) обращений к этой же процедуре:
eps:=1e-44; mm:=4; x00:=-1000; x11:=1000; y00:=-1000; y11:=1000; eps0:= 4.9; h:=eps0/43;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
В более простом случае, когда корни не выходят из квадрата со «средней» длиной стороны и они взаимно отделены в действительной или мнимой части на ≥0.1, для их вычисления достаточно одного обращения к процедуре identif1 (как в программе korkompmin примера 1). Это не исключает дополнительного циклического уточнения с помощью той же процедуры.
Пример 3. Пусть требуется найти корни полинома 10-й степени, заданного массивами действительных и мнимых частей корней в разделе констант программы:
PROGRAM prostojprimerPOLINOM;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n00=1024; np1=10;
type vect1=array [1..4*n00] of extended; vect2=array [1..4*n00] of longint; vect3=array [1..np1] of extended;
const b: vect3 =
(-4.1,4.21,-2.1,-2,-2.221,0.102,0.203,-77,55.01,55.1);
b1: vect3 =
(-44.33,-4,2,2.202,-5,-5.1,55.001,55.1,2.101,44.135);
{описание переменных скопировано из описания программы OBLASTIKORNI примера 2}
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
{процедура sort без изменений скопирована из программы korkompmin примера 1}
procedure identif1(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended; var rex,imy: vect1; var kk:longint; var
mm:longint);
{процедура identif1 полностью без изменений скопирована из программы OBLASTIKORNI примера 2}
begin
eps:=1e-44; mm:=4; x00:=-100; x11:=100; y00:=-100; y11:=100; eps0:= 0.49; h:=eps0/43;eps00:= eps0;
writeln; writeln (' ','Приближения корней',' '); writeln;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней',' '); writeln; eps0:= eps00/10; h:=eps0/43;
for ii:= 1 to kk do begin x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
{дальнейшая часть программы OBLASTIKORNI примера 2 не используется}
readln; end.
Результат работы программы:
-7.70000000000000000E+0001 -4.10000000000000000E+0000
5.51000000000000000E+0001 0.0000…0000 -4.43300000000000000E+0001 0.0000…0000
1.02000000000000000E-0001 -2.10000000000000000E+0000
-5.10000000000000000E+0000 0.0000…0000 2.00000000000000000E+0000 0.0000…0000
-2.00000000000000000E+0000 -2.22100000000000000E+0000
2.20200000000000000E+0000 0.0000…0000 -5.00000000000000000E+0000 0.0000…0000
4.21000000000000000E+0000 2.03000000000000000E-0001
-4.00000000000000000E+0000 0.0000…0000 5.50010000000000000E+0001 0.0000…0000
5.50100000000000000E+0001 5.51000000000000000E+0001
2.10100000000000000E+0000 0.0000…0000 4.41350000000000000E+0001 0.0000…0000
Здесь поиск корней выполняется в квадрате длиной стороны 200 на комплексной плоскости с центром в начале координат. Предыдущая программа OBLASTIKORNI взята практически без изменений. Исключение составляют: задание на входе полинома 10-й степени вместо бывшего полинома 45-й степени, область поиска – квадрат 200×200 вместо квадрата 2000×2000. Кроме того, в разделе инструкций из всех предыдущих обращений к процедуре identif1 оставлены только одно начальное и соответственное ему циклическое обращение для уточнения корней. В результате все корни в квадрате 200×200 идентифицированы без погрешности в формате представления данных, при этом действительные части некоторых корней попарно отделялись на 0.1, в частности при совпадении мнимых частей. Аналогично характеризуется попарная отделенность мнимых частей. В таком виде программа инвариантна в границах рассматриваемых ограничений и работает с приемлемой временной сложностью. Ниже будет представлен вариант ее максимального распараллеливания.
О временной сложности программы
Наибольшее замедление программы может вызвать неудачный выбор числовых параметров. В изложенных вариантах можно было бы использовать более высокую точность, например с границей погрешности eps=1.1e-144, а также большее количество элементов сетки при спуске, например mm=444; Однако фактически это не повысило бы точность идентификации корней, но существенно увеличило бы время работы программы. Примерно то же можно отнести к параметрам сужения окрестности корня при спуске, а также к количеству сортируемых элементов (nn0). Ключевым параметром программы, в частности в отношении длительности ее выполнения, является радиус локализации eps0 (ε0). Если его взять избыточно малым, то корни будут с необходимостью найдены, но время выполнения программы возрастет до неприемлемых значений, по крайней мере на персональном компьютере. Поэтому целесообразно придерживаться схемы, изложенной выше и реализованной для трех программ. Если степень полинома не совпадет с числом найденных корней, следует выполнить поиск корней в окрестности ранее найденных, взяв границы области вокруг действительной и мнимой части каждого с отступом на значение радиуса, при котором они были идентифицированы. Непосредственно поиск в этом случае нужно выполнять с радиусом локализации примерно в 10 раз меньше исходного. Если по-прежнему число корней меньше степени, процесс желательно повторить с учетом границ области корней и структуры их расположения. Если повторился тот же результат, требуется проверить кратность корней. Для проверки кратности изложенным способом идентифицируются все корни производной полинома, среди которых затем выполняется поиск совпадения с корнями исходного полинома. Проще подставить его корни в выражение производной.
Временная сложность параллельной идентификации корней полинома с комплексными коэффициентами
Приняты обозначения, использованные для схемы максимально параллельной идентификации действительных корней [1]. Ниже параллельное преобразование рассматривается для алгоритма, представленного программой korkompmin примера 1. В алгоритм внесено изменение: сортировка слиянием всюду заменена сортировкой подсчетом, описанной в [1]. Последовательная сортировка слиянием имеет временную сложность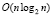 
, допускает преобразование к параллельной форме с временной сложностью 
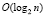. Сортировка подсчетом в максимально параллельной форме имеет единичную временную оценку 
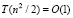, непосредственно ниже она именуется просто сортировкой.
Сначала формируется входной массив из дискретизированных наименьших значений. Наименьшее значение на каждом шаге определяется с помощью сортировки. Синхронно по всем шагам за время O(1) определяются n входных элементов (n=nn0). С учетом числа процессоров временная сложность данной операции оценится как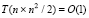 
или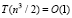 
. Вслед за тем локализуется абсцисса точки минимума. Очевидно, условие локализации можно применить взаимно независимо и синхронно к n входным индексам всех элементов полученного массива. Тогда множество всех абсцисс приближений точек минимумов идентифицируется с оценкой 
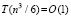. Для каждой локализованной абсциссы xk приближения точки минимума процесс повторяется одновременно для всех n дискретизированных ординат в каждом квадрате H×H. Для поиска соответственных xk ординат yk этот процесс требуется воспроизводить в каждом квадрате H×H фиксированного по значению xk вертикального слоя. В одном квадрате ординаты могут идентифицироваться одновременно по всем n шагам, ничто не мешает формальному выполнению такого же процесса одновременно во всех квадратах вертикального слоя. В отдельно взятом квадрате (теперь уже без априорной минимизации) это выполнимо с оценкой 
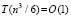. Синхронная обработка вертикальных срезов всех квадратов фиксированного слоя требует того же числа процессоров, умноженного на количество отрезков длины hh. Длина hh равна стороне квадрата, как и в случае действительных корней [1], искомое количество выразится через радиус локализации и составит 
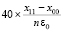. С таким коэффициентом оценка временной сложности максимально параллельной идентификации всех ординат yk для одной абсциссы xk примет вид:
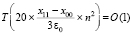. (2)
Для всех априори найденных абсцисс xk в одном квадрате H×H идентификацию ординат можно выполнить синхронно и взаимно независимо, процесс можно так же синхронно и взаимно независимо воспроизвести по всем квадратам соответственных вертикальных срезов. Множеству всех рассматриваемых абсцисс xk из одного квадрата соответствует произведение числа процессоров из (2) на количество квадратов вертикального слоя с коэффициентом n. Искомый множитель равен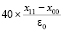 
. Сумма по всем квадратам горизонтального слоя увеличит множитель до 
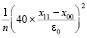. С таким множителем надо взять число процессоров в левой части (2). Отсюда максимально параллельная идентификация всех приближений корней (xk, yk) по идентифицированным абсциссам изменит оценку (2) в сторону следующего увеличения числа процессоров:
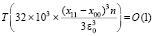. (3)
Уточняющий спуск к каждой точке приближения корня можно провести синхронно по всем приближениям (xk, yk), выбирая наименьшее значение на каждом шаге спуска с помощью сортировки применительно к m элементам сетки. Число r последовательных шагов спуска от локализованного минимума (по одной переменной) с радиусом ε0 к его приближению с заданной границей погрешности ε определяется сужением радиуса локализации в d > 1 раз на шаге. Отсюда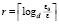 
, временная сложность отдельного спуска – 
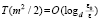. Спуск потребуется одновременно для всех приближений корней полинома, с учетом (3) оценку временной сложности всех операций параллельного спуска можно представить в виде
.
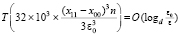Здесь число приближений корней и, соответственно, число процессоров в левой части завышено. Не умаляя общности, можно считать, что это число заведомо обеспечивает параллельный спуск, синхронно выполняемый в окрестности каждого приближения корня. Выражение правой части по величине порядка не изменится, несмотря на учет четырехкратного повтора операции спуска к каждому корню. Поэтому окончательная оценка временной сложности максимально параллельной идентификации всех комплексных корней полинома примет вид:
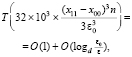
или
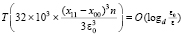. (4)
Оценка (4) дана для максимально параллельной формы. Для распараллеливания алгоритма с меньшим, в частности фиксированным, количеством процессоров имеются различные возможности. Одна из них – естественный параллелизм алгоритма по всем квадратам H×H.
Идентификация нулей функций двух действительных переменных и функций комплексной переменной
Чтобы идентифицировать нули рассматриваемых функций, можно воспользоваться программой примера 3. Изменения состоят в задании конкретной подпрограммы-функции и области поиска. Так, чтобы вычислить нули функции
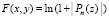, (5)
где Pn(z) – полином, заданный массивами действительных и мнимых частей в разделе констант программы prostojprimerPOLINOM данного примера, достаточно в этой программе задать функцию следующим образом:
function func (x,y:extended):extended;
var p: extended; i1: integer;
begin
p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func:=abs(Ln(1+abs(p)));
end;
Нули функции (5) по построению совпадают с корнями полинома примера 3. Действительно, результат работы программы полностью повторит результат программы примера 3: выдаст корни того же полинома с той же точностью. Аналогично идентифицируются нули функции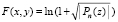 
. Такой результат, однако, никаким способом не удается получить для функций, которые в формате с плавающей точкой вычисляются с существенными потерями значащих цифр мантиссы. Так, для функции
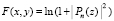(6)
по последней программе получатся все приближения корней, на которых достигаются нулевые (в формате представления данных) значения F(x, y). Но при этом приближения корней имеют в представлении мантиссы неправильные значащие цифры младших разрядов. Это затруднение можно преодолеть по аналогии со случаем одной действительной переменной [1], если известна другая функция, у которой корни совпадают с корнями исследуемой функции, но сама она при вычислении допускает идентификацию корней с более высокой точностью. В данном случае по отношению к функции (6) требуемую роль может играть функция (5). Помимо подпрограммы, реализующей вычисление основной функции (6) (в программе ниже она называется func1), организуется подпрограмма (func), которая полностью совпадет с прототипом для функции (5). Программа prostojprimerPOLINOM без изменений описанного выше примера вычисляет нули функции (5), а на выходе подставляет их значения в функцию (6), т.е. выводит func1 в найденных значениях. Результат снова повторит результат примера 3 и с той же точностью. Во избежание недоразумений модифицированная программа приводится полностью. Все изменения относительно прототипа выделены курсивом:
PROGRAM FUNCPOLINOMutochnenie;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n00=1024; np1=10;
type vect1=array [1..4*n00] of extended; vect2=array [1..4*n00] of longint; vect3=array [1..np1] of extended;
const b: vect3 =
(-4.1,4.21,-2.1,-2,-2.221,0.102,0.203,-77,55.01,55.1);
b1: vect3 =
(-44.33,-4,2,2.202,-5,-5.1,55.001,55.1,2.101,44.135);
var i,ii,j,k,kk,k1,r,ee,ee1,tty,nn0,mm: longint; c,a1,rex,imy: vect1;e,e3,e33: vect2;
aaa,x,x0,xk,xk0,xk1,hx,hy,min,eps1,eps11,eps12,eps13,z,z1,bbb,
y,y0,yk,yk0,yk1,ykk0,hh,yz,yz1,x00,x11,y00,y11,eps0,h,eps00,eps:extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
type
vecc=array[0..4*n00] of longint; var ab: integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;
begin
p:= trunc(ln(nn0)/ln(2)); if p <> ln(nn0)/ln(2) then p := p+1;
n:= round(exp(p*ln(2))); for l := 1 to n do if l<=nn0 then e[l] := l else ab:=1;
for r := 1 to p do begin m :=round(exp(r*ln(2))); nm:=n div m;
for k := 0 to nm-1 do begin for l := 1 to m div 2 do begin
if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab := l else e1[l] := e[k * m + l];
if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab := 1 else e2[l] := e[k * m + m div 2 + l]
end; i := 1; j := 0; while i + j <= m do begin if i = m div 2 + 1 then ab := -1; if j = m div 2 then ab := 1;
if (k * m + i > nn0) or (e[k * m + i]>nn0) or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)
then ab:=1; if (i <= m div 2) and (j <= m div 2 -1) and (k * m + i<= nn0) and (k * m + m div 2 + j <= nn0-1)
then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab := 1 else begin if c[e2[j + 1]] - c[e1[i]]= 0 then ab := 0;
if c[e2[j + 1]] - c[e1[i]]> 0 then ab := 1; if c[e2[j + 1]] - c[e1[i]]< 0 then ab := -1 end; if ab >= 0 then
begin e[k * m + i + j] := e1[i]; i := i + 1 end else begin e[k * m + i + j] := e2[j + 1]; j := j + 1 end
end end end end;
function func1 (x,y:extended):extended;
var p: extended; i1: integer;
begin
p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func1:=abs(Ln(1+sqr(abs(p))));
end;
procedure identif1(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended;
var rex,imy: vect1;var kk:longint;var mm:longint);
label 21,22,23;
function func (x,y:extended):extended;
var p: extended; i1: integer;
begin
p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func:=abs(Ln(1+abs(p)));
end;
procedure minx (var x,y,min:extended;var ee:integer);
begin min:=func(x,y); ee:=0; for i:=1 to mm do begin x:=xk0+i*hx;
if min > func(x,y) then begin min:=func(x,y);ee:=i end end end;
procedure miny (var x,y,min:extended;var ee1:integer);
begin min:=func(x,y); ee1:=0; for i:=1 to tty do begin y:=ykk0+i*hy;
if min > func(x,y) then begin min:=func(x,y);ee1:=i end end end;
procedure spuskx( var eps1, xk0,xk1,hx,y: extended);
begin while abs(eps1) > eps do begin x:=xk0; minx (x,y,min,ee); eps1:=eps1/1.2;
xk0:=xk0+ee*hx-eps1;xk1:=xk0+eps1;hx:=abs(2*eps1)/mm end end;
procedure spusky(var eps11,yk0,yk1,hy,x: extended);
begin while abs(eps11) > eps do begin ykk0:=yk0; y:=yk0; tty:=mm;
miny (x,y,min,ee1); eps11:=eps11/1.2; yk0:=yk0+ee1*hy-eps11; yk1:=yk0+eps11;
hy:=abs(2*eps11)/mm end end;
begin
aaa:=1e62; bbb:=1e62; kk:=0; x0:=x00; y0:=y00; nn0:=n00; hh:=nn0*h;
while x0 <= x11+hh do begin while y0 <= y11+hh do begin
for r:=1 to nn0 do begin x:=x0+r*h; ykk0:=y0; y:=y0; tty:=n00; hy:=h; miny (x,y,min,ee1); a1[r]:=min end;
sort( nn0, a1, e3); k:=1; while k<= nn0 do begin
for r := 1 to k-1 do if abs(e3[k]-e3[k-r]) <=eps0/h then goto 23; xk:= x0+e3[k]*h;
for r:=1 to nn0 do begin y:=y0+r*h; a1[r]:=func(xk,y) end;
sort( nn0, a1, e33); k1:=1; while k1<= nn0 do begin
for r := 1 to k1-1 do if abs(e33[k1]-e33[k1-r])<=eps0/h then goto 22; yk:= y0+e33[k1]*h;
eps1:=eps0; eps11:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; hx:=abs(2*eps1)/mm; y:=yk;
spuskx(eps1,xk0,xk1,hx,y); yk0:=yk-eps11; yk1:=yk+eps11; hy:=abs(2*eps11)/mm; x:=xk0+ee*hx+eps1;
spusky( eps11,yk0,yk1,hy,x); eps12:=eps0/1.2; xk0:=x-eps12; xk1:=x+eps12; hx:=abs(2*eps12)/mm;
y:=yk0+ee1*hy+eps11; spuskx( eps12, xk0,xk1,hx,y); eps13:=eps0/1.2;
yk0:=yk0+ee1*hy-eps13; yk1:=yk0+2*eps13; hy:=abs(2*eps13)/mm;
x:=xk0+ee*hx+eps12; spusky( eps13,yk0,yk1,hy,x);
if func(xk,yk)= 0 then begin x:=xk; yk0:=yk; goto 21 end;
for i:= 1 to 2 do begin z:=x+i*h; if func(x,yk0) >= func(z,yk0) then goto 23; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x,yk0) >= func(z1,yk0) then goto 23; end;
for i:= 1 to 2 do begin yz:=yk0+i*h; if func(x,yk0) >= func(x,yz) then goto 22; end;
for i:= 1 to 2 do begin yz1:=yk0-i*h; if func(x,yk0) >= func(x,yz1) then goto 22; end;
if abs(aaa-x)<=1e-50 then goto 23; if abs(bbb-yk0)<=1e-50 then goto 22;
21: kk:=kk+1; rex[kk]:=x; imy[kk]:=yk0;
if func(x,yk0)<=1e-3 then begin
writeln (' ', x:30,' '); writeln (' ', yk0:30,' ', func1(x,yk0):30); writeln; aaa:=x; bbb:=yk0; end;
22: k1:=k1+1 end;
23: k:=k+1 end; y0:=y0+hh end; x0:=x0+hh; y0:=y00 end;
end;
begin
eps:=1e-44; mm:=4; x00:=-100; x11:=100; y00:=-100; y11:=100; eps0:= 0.49; h:=eps0/43;eps00:= eps0;
writeln;
writeln (' ','Приближения корней',' '); writeln; identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней ',' '); writeln; eps0:= eps00/10; h:=eps0/43;
for ii:= 1 to kk do begin x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln;
end.
Результатом будет вычисление нулей функции (6), полностью совпадающее с вычислением нулей функции (5) и полинома примера 3 по программе prostojprimerPOLINOM:
-7.70000000000000000E+0001 -4.10000000000000000E+0000
5.51000000000000000E+0001 0.0000…0000 -4.43300000000000000E+0001 0.0000…0000
…………………………………………………………………………………………………………
5.50100000000000000E+0001 5.51000000000000000E+0001
2.10100000000000000E+0000 0.0000…0000 4.41350000000000000E+0001 0.0000…0000
Замечание 1. В качестве уточняющей функции может использоваться произвольная функция (func), имеющая искомые корни, которая дает правильную компьютерную идентификацию в формате представления данных. В частности, для функции (6) (func1) вместо функции (5) можно использовать функцию (1) при значениях из раздела констант. Менее тривиально применить прием для сложной суперпозиции с вложенной уточняющей функцией, или в случае, когда суперпозиция и вложение априори не известны, например появляются в неявном виде по ходу решения некоторой задачи.
Замечание 2. Если в программе FUNCPOLINOMutochnenie обе подпрограммы func и func1 взять одинаковыми, то программы FUNCPOLINOMutochnenie и prostojprimerPOLINOM окажутся построенными одинаково и дадут одинаковый результат для одной и той же входной функции func. В этом случае задавать дополнительно func1 излишне. Поскольку код FUNCPOLINOMutochnenie выше приведен полностью, то именно на эту программу будут дальнейшие ссылки с оговоркой относительно совпадения (или напротив) функций func и func1.
С точностью до замечания 2 данный прием не универсален, но во многих случаях его применение дает положительный результат.
Пример 4. Пусть требуется найти корни функции
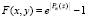, (7)
где Pn(z) по-прежнему из (1) со значениями корней из программы примера 3, использованными непосредственно выше. Если в программе FUNCPOLINOMutochnenie заменить функцию (6) (func1:=abs(Ln(1+sqr(abs(p))));) на функцию (7) (func1:=abs(exp(p)-1);), больше ничего не меняя, в частности сохранив func:=abs(Ln(1+abs(p))); то результат работы программы не изменится. Она выдаст 10 комплексных корней из примера 3 со всеми правильными значениями разрядов мантиссы в формате представления данных. Если же данным приемом не воспользоваться, а в процедуре identif1 непосредственно задать функцию (7) (func:=abs(exp(p)-1);) и выводить также значения func, то программа будет выдавать нулевые значения в корнях этой функции, но значащие цифры мантисс действительной и мнимой части корней изменятся до неузнаваемости. Хотя они все же сохранят не менее 6 верных значащих цифр.
Следующий пример относится к случаю, когда рассматриваемый прием неприменим.
Пример 5. Требуется найти нули функции комплексной переменной
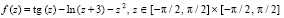. (8)
У функции (8) можно определить сумму квадратов 
и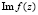 
(например, с помощью Maple):
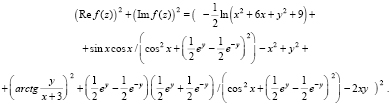(9)
Выражение (9) задается на входе программы FUNCPOLINOMutochnenie:
func:=sqr(-1/2*ln(x*x+6*x+9+y*y)+sin(x)*cos(x)/(cos(x)*cos(x)+sqr(1/2*exp(y)-1/2*exp(-y)))-x*x+y*y)+
sqr(-arctan(y/(x+3))+(1/2*exp(y)-1/2*exp(-y))*(1/2*exp(y)+1/2*exp(-y))/(cos(x)*cos(x)+
sqr(1/2*exp(y)-1/2*exp(-y)))-2*x*y);
func1 задается точно в таком же виде. Уточнение нулей будет происходить с использованием самой функции (9) согласно замечанию 2. Входные параметры в разделе инструкций:
eps:=1e-44; mm:=4; x00:=-pi/2; x11:=pi/2; y00:=-pi/2; y11:=pi/2; eps0:= 0.049; h:=eps0/43;eps00:= eps0;
Для наглядности расширен формат вывода данных:
writeln (' ', x:2:30,' '); writeln (' ', yk0:2:30,' ', func1(x,yk0):2:30);
Больше ничего в программе не меняется. Результат работы программы:
0.221997368779427950000000000000
-1.092838547912587950000000000000 0.000000000000000000000000000000
0.221997368779427950000000000000
1.092838547912587950000000000000 0.000000000000000000000000000000
1.249979418341933270000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
Приближенно найдены пара комплексно сопряженных корней и один действительный корень.
Идентификация корней характеристического полинома матрицы с приложением к анализу устойчивости
Собственные числа матрицы ниже вычисляются как корни характеристического полинома, коэффициенты которого определяются по методу Леверье решения полной проблемы собственных значений [6, 11, 12]. Пусть рассматривается однородная система
Ax = λx (10)
с матрицей A, n×n и требуется найти все λ, при которых решения системы (10) являются нетривиальными. Как известно, условием для этого является выполнение соотношения
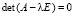. (11)
Характеристическое уравнение (11) для матрицы A записывается в форме уравнения, левая часть которого – характеристический полином с неопределенными коэффициентами
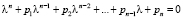. (12)
Для нахождения коэффициентов вычисляются следы всех степеней матрицы A
, 
, 
, 
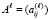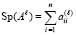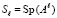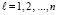, (13)
В (13) след матрицы Al, обозначаемый Sp(Al), – сумма ее диагональных элементов. Следы и искомые коэффициенты связаны уравнениями Ньютона
, 
.
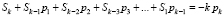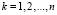Эти уравнения разворачиваются в рекуррентную систему
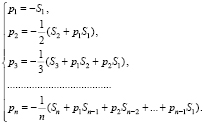(14)
Из (14) последовательно определяются искомые коэффициенты. Представленные компоненты этого метода запрограммированы ниже. Вычисление коэффициентов – часть программы. Как только коэффициенты найдены, для решения уравнения (12) можно применять идентификацию корней полинома на основе сортировки слиянием, ниже приводится программа. Ее параметры выбраны для примера, в случае полиномов с числовыми коэффициентами программа работает со всеми допустимыми соотношениями параметров, описанными выше.
program LeverieUtochnenie;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n1=6{4}; n00=1512;
type vect=array[0..n1] of extended; matr=array[1..n1,1..n1] of extended;
vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;
vect3=array [0..n1] of extended;
{примеры матриц, обрабатывается незакомментированная матрица}
const aa:matr ={ ((-1,-0.09, 0.077,-0.001),
(0.087,-0.9, 0.005, 0.019),
(-0.034,0.034,-0.2,-0.06),
(0,-0.022,0.092,-1.4)); }
{ ((1,-0.09, 0.077,-0.001),
(0.087,0.9, 0.005, 0.019),
(-0.034,0.034,0.2,-0.06),
(0,-0.022,0.092,1.4)); }
{ ((0, 1, 0, 0, 0, 0),
(0, 0, 1, 0, 0, 0),
(0, 0, 0, 1, 0, 0),
(0, 0, 0, 0, 1, 0),
(0, 0, 0, 0, 0, 1),
(4, 0, 7, 0, 2, 0)); } {(t^2+1)^2(t^2-4)}
((0, 1, 0, 0, 0, 0),
(0, 0, 1, 0, 0, 0),
(0, 0, 0, 1, 0, 0),
(0, 0, 0, 0, 1, 0),
(0, 0, 0, 0, 0, 1),
(-4, -16, -25, -20, -10, -4)); {(t+1)^4(t^2+4)}
var cc,cc1: matr; ep,pp: vect; c,a1,rex,imy: vect1; e,e3,e33: vect2; i,j,k,k1,r,ee,ee1,tty,nn0,mm: longint;
ii,jj,kk,ll,kratn: integer; bdv,bmv,bd,bm,da,db: vect3;
ss,ss1,a,b,a11,b11,ca,cb,y,y0,y1,yk,yk0,yk1,ykk0,hh,aaa,bbb, z,z1,yz,yz1,x,x0,x1,xk,xk0,xk1,
hx,hy,min,eps1,eps11,eps12,eps13,eps0,h,x00,x11,y00,y11,eps,eps00: extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
{процедура sort без изменений скопирована из программы FUNCPOLINOMutochnenie (korkompmin
примера 1)}
{аналог процедуры identif1 для характеристического полинома}
procedure identif11(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended; var rex,imy: vect1; var kk,mm:longint);
label 21,22,23;
var kk1:longint;
{комплексное умножение}
procedure um(var a,b,a11,b11: extended; var ca,cb: extended);
begin ca:=a*a11-b*b11; cb:=a*b11+b*a11 end;
{комплексное сложение}
procedure sum(var a,b,a11,b11: extended; var ca,cb: extended);
begin ca:=a+a11; cb:=b+b11 end;
{аналог схемы Горнера для вычисления комплексного значения полинома,
выделение его действительной и мнимой части, определение суммы квадратов
действительной и мнимой части, вычисление модуля полинома}
function func (var x,y: extended; var bdv, bmv: vect3): extended;
var i1: 0..n1; p1,p2,pp1,pp2,d1,d2,d3,d4:extended;
begin p1:=bdv[n1]; p2:=bmv[n1]; for i1:=1 to n1 do begin um(p1,p2,x,y,d1,d2);
pp1:=bdv[n1-i1];pp2:=bmv[n1-i1]; sum(pp1,pp2,d1,d2,d3,d4); p1:=d3; p2:=d4; end;
func:=sqrt(sqr(p1)+sqr(p2)); end;
procedure minx (var x,y,min:extended;var ee:longint);
begin min:=func(x,y,bdv,bmv); ee:=0; for i:=1 to mm do begin x:=xk0+i*hx;
if min > func(x,y,bdv,bmv) then begin min:=func(x,y,bdv,bmv); ee:=i end end end;
procedure miny (var x,y,min: extended; var ee1: longint);
begin min:=func(x,y,bdv,bmv); ee1:=0; for i:=1 to tty do begin y:=ykk0+i*hy;
if min > func(x,y,bdv,bmv) then begin min:=func(x,y,bdv,bmv); ee1:=i end end end;
procedure spuskx (var eps1, xk0,xk1,hx,y: extended);
begin while abs(eps1) > eps do begin x:=xk0; minx (x,y,min,ee); eps1:=eps1/1.2;
xk0:=xk0+ee*hx-eps1;xk1:=xk0+eps1;hx:=abs(2*eps1)/mm end end;
procedure spusky (var eps11,yk0,yk1,hy,x: extended);
begin while abs(eps11) > eps do begin ykk0:=yk0; y:=yk0; tty:=mm; miny (x,y,min,ee1);
eps11:=eps11/1.2; yk0:=yk0+ee1*hy-eps11; yk1:=yk0+eps11; hy:=abs(2*eps11)/mm end end;
{вычисление текущей степени матрицы A}
procedure ummatr (const aa:matr;var cc,cc1:matr);
var ss: extended; ii,jj,l1: integer;
begin for ii:=1 to n1 do for jj:=1 to n1 do begin ss:=0; for l1:=1 to n1 do
ss:=ss+cc[ii,l1]*aa[l1,jj]; cc1[ii,jj]:=ss; end; end;
{реализация метода Леверье}
begin
{степени матриц и их следы}
ss1:=0; for ii:=1 to n1 do ss1:=ss1+aa[ii,ii]; ep[1]:=ss1; for ii:=1 to n1 do for jj:=1 to n1 do cc[ii,jj]:=aa[ii,jj];
for kk1:=2 to n1 do begin ummatr (aa, cc,cc1); for ii:=1 to n1 do for jj:=1 to n1 do cc[ii,jj]:=cc1[ii,jj];
ss1:=0; for ii:=1 to n1 do ss1:=ss1+cc[ii,ii]; ep[kk1]:=ss1; end;
{рекуррентное нахождение коэффициентов характеристического полинома из уравнений Ньютона}
pp[1]:=-ep[1]; for kk1:=2 to n1 do
begin ss:=ep[kk1]; for ll:=1 to kk1-1 do ss:=ss+ep[kk1-ll]*pp[ll]; pp[kk1]:=-1/kk1*ss; end;
pp[0]:=1; for i:=0 to n1 do bd[i]:=pp[n1-i]; for i:=0 to n1 do bm[n1-i]:=0;
writeln; writeln (' ', 'koeffitcienti harakterist polinoma:',' ');writeln;
for kk1:=0 to n1 do writeln (' ':2,pp[kk1]:2:30); writeln;
{коэффициенты характеристического полинома (kratn:=1) и его производных
(kratn:=2; kratn:=3; kratn:=4) для учета кратности его корней}
kratn:=1;
case kratn of
1: begin for i:=0 to n1 do bdv[i]:=bd[i]; for i:=0 to n1 do bmv[i]:=bm[i];
writeln; writeln (' ', 'korni: '); writeln; end;
2: begin for i:=1 to n1 do bdv[i-1]:=i*bd[i]; for i:=1 to n1 do bmv[i-1]:=i*bm[i];
writeln; writeln (' ', 'koeffitcienti 1 proizv:',' '); writeln;
pp[0]:=1; for kk1:=0 to n1 do writeln (' ':2,(n1-kk1)*pp[kk1]:2:30); writeln;
writeln; writeln (' ', 'korni: '); writeln; end;
3: begin writeln; writeln (' ', 'koeffitcienti 2 proizv:',' '); writeln;
pp[0]:=1; for kk1:=0 to n1 do writeln (' ':2,(n1-kk1)*(n1-kk1-1)*pp[kk1]:2:30); writeln;
writeln; writeln (' ', 'korni: '); writeln;
for i:=2 to n1 do bdv[i-2]:=i*(i-1)*bd[i]; for i:=3 to n1 do bmv[i-2]:=i*(i-1)*bm[i];end;
4: begin writeln; writeln (' ', 'koeffitcienti 3 proizv:',' '); writeln;
pp[0]:=1; for kk1:=0 to n1 do writeln (' ':2,(n1-kk1)*(n1-kk1-1)*(n1-kk1-2)*pp[kk1]:2:30); writeln;
writeln; writeln (' ', 'korni: ');writeln;
for i:=3 to n1 do bdv[i-3]:=i*(i-1)*(i-2)*bd[i]; for i:=3 to n1 do bmv[i-3]:=i*(i-1)*(i-2)*bm[i]; end;
end;
{идентификация корней характеристического полинома (корней его производных)}
nn0:=n00; hh:=nn0*h; x0:=x00; x1:=x11; y0:=y00; y1:=y11;
while x0 <= x1+hh do begin while y0 <= y1+hh do begin
for r:=1 to nn0 do begin x:=x0+r*h; ykk0:=y0; y:=y0; tty:=n00;hy:=h; miny (x,y,min,ee1);
a1[r]:=min end; sort (nn0, a1, e3); k:=1; while k<= nn0 do begin
for r := 1 to k-1 do if abs (e3[k]-e3[k-r]) <= eps0/h then goto 23; xk:= x0+e3[k]*h;
for r:=1 to nn0 do begin y:=y0+r*h; a1[r]:=func (xk,y,bdv,bmv) end;
sort (nn0, a1, e33); k1:=1; while k1<= nn0 do begin
for r := 1 to k1-1 do if abs(e33[k1]-e33[k1-r]) <=eps0/h then goto 22; yk:= y0+e33[k1]*h;
eps1:=eps0; eps11:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; hx:=abs(2*eps1)/mm; y:=yk;
spuskx (eps1,xk0,xk1,hx,y); yk0:=yk-eps11; yk1:=yk+eps11; hy:=abs(2*eps11)/mm; x:=xk0+ee*hx+eps1;
spusky ( eps11,yk0,yk1,hy,x); eps12:=eps0/1.2; xk0:=x-eps12; xk1:=x+eps12; hx:=abs(2*eps12)/mm;
y:=yk0+ee1*hy+eps11; spuskx( eps12, xk0,xk1,hx,y); eps13:=eps0/1.2;
yk0:=yk0+ee1*hy-eps13; yk1:=yk0+2*eps13; hy:=abs(2*eps13)/mm;
x:=xk0+ee*hx+eps12; spusky( eps13,yk0,yk1,hy,x);
if func (xk,yk,bdv,bmv)= 0 then begin x:=xk; yk0:=yk; goto 21 end;
for i:= 1 to 2 do begin z:=x+i*h; if func (x,yk0,bdv,bmv) >= func (z,yk0,bdv,bmv) then goto 23; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func (x,yk0,bdv,bmv) >= func (z1,yk0,bdv,bmv) then goto 23; end;
for i:= 1 to 2 do begin yz:=yk0+i*h; if func (x,yk0,bdv,bmv) >= func (x,yz,bdv,bmv) then goto 22; end;
for i:= 1 to 2 do begin yz1:=yk0-i*h; if func (x,yk0,bdv,bmv) >= func (x,yz1,bdv,bmv) then goto 22; end;
kk:=kk+1; rex[kk]:=x; imy[kk]:=yk0;
if abs(aaa-x)<=1e-50 then goto 23; if abs(bbb-yk0)<=1e-50 then goto 22;
21: if abs( func(x,yk0,bdv,bmv))<=1e-3{15} then
begin writeln (' ', x:2:30,' '); writeln (' ', yk0:2:30,' ', func(x,yk0,bdv,bmv):2:30); writeln;
aaa:=x; bbb:=yk0; end;
22: k1:=k1+1 end;
23: k:=k+1 end;
y0:=y0+hh end; x0:=x0+hh; y0:=y00 end; end;
{блок инструкций}
begin
eps:=1e-44; mm:=4; x00:=-10; x11:=10; y00:=-10; y11:=10; eps0:=0.09; h:=eps0/43; eps00:= eps0;
writeln; writeln (' ','Приближения корней',' '); writeln;
identif11(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения корней',' '); writeln; eps0:= eps00/10; h:=eps0/43; for ii:= 1 to kk do
begin x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif11(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln
end.
Программа LeverieUtochnenie вычисляет все собственные числа незакомментированной матрицы с учетом их кратности. Для этого формируются коэффициенты характеристического полинома, поиск его корней соответствует параметру kratn:=1; оператора case kratn of. Коэффициенты вычисляются согласно (12)–(14) в блоке реализации метода Леверье. Степени входной матрицы образуются в цикле с использованием процедуры ummatr (aa, cc,cc1). Следы степеней определяются как значение ep[kk] в цикле по kk (Sp(Al) получается при l = kk). Коэффициенты характеристического полинома определяются в цикле: pp[1]:=-ep[1]; for kk:=2 to n1 do begin ss:=ep[kk]; for ll:=1 to kk-1 do ss:=ss+ep[kk-ll]*pp[ll]; pp[kk]:=-1/kk*ss; end; В блоке pp[0]:=1; for kk:=0 to n1 do writeln (' ':2,pp[kk]:2:30); writeln; for i:=0 to n1 do bd[i]:=pp[n1-i]; for i:=0 to n1 do bm[n1-i]:=0; коэффициенты перенумеровываются по убыванию показателей степеней характеристического полинома. Аналог схемы Горнера строится следующим образом. Полином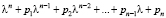 
переписывается в виде 
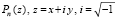с новым обозначением коэффициентов:
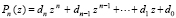. (15)
В программе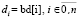 
. Для (15) схема Горнера эквивалентна расстановке скобок:
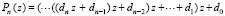. (16)
Если бы z было действительным, то (15) выполнялось бы в цикле: P:=d[n]; for i:=1 to n do P:=P*z+ d[n-i]; В рассматриваемом случае арифметические операции являются комплексными. Поэтому формируются процедуры комплексного умножения um(a,b,a11,b11,ca,cb) и комплексного сложения sum(a,b,a11,b11,ca,cb). Эти процедуры выполняются в порядке действий (16), однако их запись сложнее и выполнение осуществляет подпрограмма-функция: func (x,y,bdv,bmv). Функция func формирует действительную и мнимую части полинома (16) p1:=d3; p2:=d4; сумму их квадратов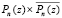 
и модуль полинома 
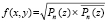: func:=sqrt(sqr(p1)+sqr(p2)); Дальнейший поиск корней функции f(x, y) не отличается от поиска, описанного применительно к (1) в разделе «Идентификация нулей функций двух действительных переменных и функций комплексной переменной …».
Результат работы программы LeverieUtochnenie (промежуточные данные опускаются):
Коэффициенты характеристического полинома:
1.000000000000000000000000000000 4.000000000000000000000000000000
10.000000000000000000000000000000 20.000000000000000000000000000000
25.000000000000000000000000000000 16.000000000000000000000000000000
4.000000000000000000000000000000
Корни характеристического полинома:
-1.000000040126996730000000000000
0.000000000171374580000000000000 0.000000000000000000000000000000
0.000000000000000000000000000000
-2.000000000000000000000000000000 0.000000000000000000000000000000
0.000000000000000000000000000000
2.000000000000000000000000000000 0.000000000000000000000000000000
Число корней меньше степени полинома, поэтому выполняется проверка кратности корней.
Коэффициенты первой производной (kratn:=2;) характеристического полинома:
6.000000000000000000000000000000 20.000000000000000000000000000000
40.000000000000000000000000000000 60.000000000000000000000000000000
50.000000000000000000000000000000 16.000000000000000000000000000000
0.000000000000000000000000000000
Корни первой производной характеристического полинома:
-1.000000000137631700000000000000
-0.000000000232830640000000000000 0.000000000000000000000000000000
-0.166666666666666670000000000000
-1.624465724134827320000000000000 0.000000000000000010000000000000
-0.166666666666666670000000000000
1.624465724134827320000000000000 0.000000000000000010000000000000
Действительное число –1 является приближением корня полинома и его первой производной. Число корней меньше степени первой производной, выполняется проверка кратности корня этой производной.
Коэффициенты второй производной (kratn:=3;) характеристического полинома:
30.000000000000000000000000000000 80.000000000000000000000000000000
120.000000000000000000000000000000 120.000000000000000000000000000000
50.000000000000000000000000000000 0.000000000000000000000000000000
0.000000000000000000000000000000
Корни второй производной характеристического полинома:
-1.000000000000000000000000000000
-0.000000000186264510000000000000 0.000000000000000000000000000000
-0.333333333333333330000000000000
-1.247219128924647130000000000000 0.000000000000000000000000000000
-0.333333333333333330000000000000
1.247219128924647130000000000000 0.000000000000000000000000000000
Число корней равно степени второй производной. В результате действительное число –1 оказалось приближением корня полинома, его первой и второй производной. Поэтому оно является не менее чем трехкратным корнем характеристического полинома незакомментированной матрицы 6-го порядка. Но у характеристического полинома должно быть 6 корней, а на данный момент идентифицированы только 5: два комплексно сопряженных и трехкратное значение –1. Выполняется проверка кратности корня второй производной.
Коэффициенты третьей производной (kratn:=4;) характеристического полинома:
120.000000000000000000000000000000 240.000000000000000000000000000000
240.000000000000000000000000000000 120.000000000000000000000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
0.000000000000000000000000000000
Корни третьей производной характеристического полинома:
-1.000000000000000000000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
-0.500000000000000000000000000000
0.866025403784438650000000000000 0.000000000000000000000000000000
-0.500000000000000000000000000000
-0.866025403784438650000000000000 0.000000000000000010000000000000
Действительное значение –1 оказалось приближением корня полинома, его первой, второй и третьей производной. Это значение является четырехкратным корнем характеристического полинома рассматриваемой матрицы. Всего у этого полинома 6 корней: два комплексно сопряженных и четырехкратное значение –1. Все корни найдены. В программе обрабатывалась последняя сверху вниз матрица из раздела констант. Она является матрицей Фробениуса, построенной для характеристического полинома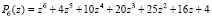 
, или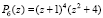 
. Комментарий в программе: {(t+1)^4(t^2+4)}. Как известно, корни полинома с коэффициентами (записанными с обратным знаком и взятыми в соответственной последовательности) из последней строки матрицы Фробениуса совпадают с собственными числами этой матрицы [4]. Действительный корень 
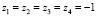является четырехкратным, мнимые корни 
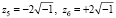являются простыми, все корни найдены правильно.
Замечание 3. Если бы рассмотренная матрица определяла матрицу коэффициентов линейной системы обыкновенных дифференциальных уравнений
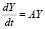, (17)
то найденные значения корней характеристического полинома (отрицательный действительный 4-кратный корень, простые сопряженные мнимые корни) означали бы неасимптотическую устойчивость системы (17) в смысле Ляпунова [6].
Замечание 4. Известно критичное свойство неустойчивости корней полинома в зависимости от погрешности коэффициентов [4, 5]. В изложенном методе коэффициенты вычисляются по трудоемкой схеме, накопление погрешности могло бы иметь следствием неточность вычисления корней. По этой причине числа в программе выводятся в расширенном формате. Для анализа устойчивости достаточно верного вычисления знака действительной части и ее приближения к нулю. Могло бы показаться, что высокая точность собственных чисел не требуется. Однако свойство неустойчивости таково, что сравнительно малая погрешность одного коэффициента может не только привести к потере знака действительной части, но и сделать комплексными все действительные корни. Поэтому необходимо вычисление коэффициентов полиномов с самой высокой точностью в формате extended.
Замечание 5. Поскольку вычисляются коэффициенты производных, кратность можно проверять подстановкой корней полинома в его производные. При необходимости можно выполнить уточнение, аналогичное уточнению корней производных.
Согласно численному эксперименту изложенный метод дает правильный результат для оценки устойчивости. Так, если перейти к предшествующей матрице программы – она также является матрицей Фробениуса, ее характеристический полином имеет вид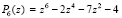 
, или, 
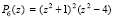(комментарий {(t^2+1)^2(t^2-4)}), результат будет следующим:
Коэффициенты характеристического полинома:
1.000000000000000000000000000000 -0.000000000000000000000000000000
-2.000000000000000000000000000000 -0.000000000000000000000000000000
-7.000000000000000000000000000000 -0.000000000000000000000000000000
-4.000000000000000000000000000000
Корни характеристического полинома:
-0.000000000164636130000000000000
-1.000000000000000000000000000000 0.000000000000000000000000000000
-2.000000000000000000000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
-0.000000000164636130000000000000
1.000000000000000000000000000000 0.000000000000000000000000000000
2.000000000000000000000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
Среди корней один имеет положительную действительную часть, это означает неустойчивость системы (17) в случае данной матрицы коэффициентов [6]. Получено 4 приближения различных корней. Если все же требуется найти оставшиеся, то следует перейти к производной (kratn:=2;). Новый результат работы программы:
Коэффициенты первой производной (kratn:=2;) характеристического полинома:
6.000000000000000000000000000000 -0.000000000000000000000000000000
-8.000000000000000000000000000000 -0.000000000000000000000000000000
-14.000000000000000000000000000000 -0.000000000000000000000000000000
-0.000000000000000000000000000000
Корни первой производной характеристического полинома:
0.000000000000000000000000000000
-1.000000000000000000000000000000 0.000000000000000000000000000000
0.000000000000000000000000000000
1.000000000000000000000000000000 0.000000000000000000000000000000
1.527525231651946670000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
-1.527525231651946670000000000000
-0.000000000000000000000000000000 0.000000000000000000000000000000
0.000000000000000000000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
Сопряженная пара мнимых корней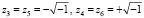 
повторилась (в данном приближении), это означает их кратность для исходного полинома (действительная часть нулевая, в этом случае кратность – еще один признак неустойчивости [6]). Производная – полином 5-й степени, вычислены 5 ее различных корней. В результате найдены все 6 корней характеристического полинома рассматриваемой матрицы с учетом кратности, их приближенные значения приводят к правильной оценке устойчивости системы (17) с данной матрицей.
Если перейти к предшествовавшей сверху матрице 4-го порядка, то программа даст следующий результат:
Коэффициенты характеристического полинома:
1.000000000000000000000000000000 -3.500000000000000000000000000000
4.236216000000000000000000000000 -2.001445140000000000000000000000
0.262744602640000000000000000000
Корни характеристического полинома:
0.948545112346407780000000000000
-0.072804250958516680000000000000 0.000000000000000000000000000000
0.948545112346407780000000000000
0.072804250958516690000000000000 0.000000000000000000000000000000
1.394764833514555520000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
0.208144941792628930000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
Все корни различны, все – с положительной действительной частью. Система (17) с такой матрицей коэффициентов неустойчива, что соответствует диагональному преобладанию положительных элементов матрицы.
Наконец, если перейти к первой сверху матрице 4-го порядка, то для характеристического полинома (kratn:=1;) результат будет следующим:
Коэффициенты характеристического полинома:
1.000000000000000000000000000000 3.500000000000000000000000000000
4.236216000000000000000000000000 2.000816860000000000000000000000
0.261925557840000000000000000000
Корни характеристического полинома:
-0.949185526306461820000000000000
-0.077266028098444620000000000000 0.000000000000000000000000000000
-0.949185526306461820000000000000
0.077266028098444610000000000000 0.000000000000000000000000000000
-1.394529097457662880000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
-0.207099849929413470000000000000
0.000000000000000000000000000000 0.000000000000000000000000000000
Приближенные значения всех четырех корней различны, у всех действительная часть отрицательна, это означает асимптотическую устойчивость системы (17) с данной матрицей коэффициентов [6]. Результат соответствует диагональному преобладанию отрицательных элементов матрицы.
О параллельной форме вычисления собственных значений матрицы на основе сортировки
Схема идентификации всех комплексных корней полинома имеет максимально параллельную форму, временная сложность которой оценивается из (4). Предварительное нахождение коэффициентов характеристического полинома по методу Леверье согласно параллельной модификации Ксанки (Csanky) [13] имеет временную сложность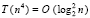 
. Объединение этой оценки с (4) влечет временную сложность параллельного вычисления корней характеристического полинома матрицы:
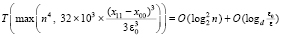. (18)
В (18) n – порядок матрицы, ε – априори заданная граница абсолютной погрешности вычислений, ε0 – радиус локализации, x11 – x00 – длина стороны квадрата, ограничивающего область корней характеристического полинома.
Об аналитических оценках области корней полинома
Представленные программы вычисления корней полинома целесообразно применять в три этапа. Вначале следует взять большой радиус локализации в заведомо расширенных границах области, чтобы с помощью программы приближенно указать реальные границы области корней. Затем с отступом от границ на выбранный радиус повторить выполнение программы с уточнением, чтобы получить представление о расположении корней. Остается задать реальные границы области с отступом от уточненных границ на радиус, с которым они получились. С новым радиусом, заведомо меньшим половины расстояния между ближайшими корнями в проекции на оси декартовых координат, можно выполнить программу с уточнением каждого корня. Априори целесообразно иметь аналитическую оценку области корней. В частности, можно использовать круги Гершгорина [11, 12]. Пусть матрица A, n×n, из (10) состоит из элементов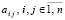 
. Согласно [11, 12] все ее собственные числа этой матрицы лежат в объединении кругов
, 
, 
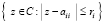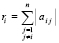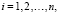(19)
где ri – сумма модулей внедиагональных элементов i-й строки.
Пусть теперь (15) – полином общего вида. Если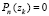 
, то
, 
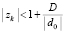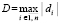, (20)
кроме того [5],
, 
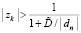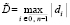. (21)
Для случая dn = 1 в [5] приводится также оценка Вестерфильда:
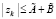, (22)
где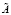 
и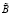 
– два наибольших числа в последовательности 
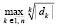. Оценки (19)–(22) можно дополнить еще одной простой оценкой. Не умаляя общности, можно считать старший коэффициент полинома равным единице,
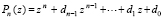. (23)
Корни 
полинома (23) являются собственными значениями матрицы Фробениуса
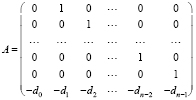. (24)
Для матрицы (24) справедливы теорема Гершгорина и оценки (19), согласно которым ее собственные значения лежат в объединении кругов
: 
, 
,
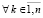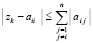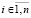или, с учетом нулевых элементов диагонали (24), и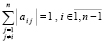 
,
, 
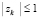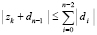. (25)
Поскольку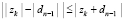 
, то из (25) 
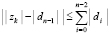. Отсюда
: 
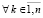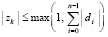. (26)
Теорема 1. Все корни полинома (23) лежат в объединении кругов (25) и оцениваются через его коэффициенты из неравенства (26).
Следствие 1. Если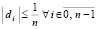 
, то все корни полинома (23) не выходят из единичного круга: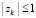 
.
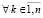На основе теоремы 1 можно получить оценки области собственных значений через следы степеней матрицы. Систему (14) можно записать в матрично-векторной форме
, 
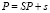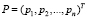, (27)
где
, 
, 
, 
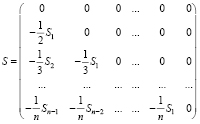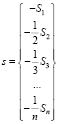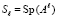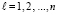. (28)
Из (27), (28)
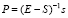. (29)
В (29) E – единичная матрица, S – нижняя треугольная с нулевой диагональю. Поэтому [14]
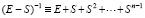. (30)
С использованием (30)
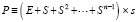. (31)
Ниже используется каноническая норма вектора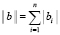 
. Для левой части (29) верна оценка (26) в обозначении 
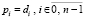. В данном обозначении для вектора коэффициентов характеристического полинома и его корней λk оценку (26) можно записать в виде
: 
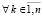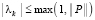. (32)
Подстановка сюда правой части (31) влечет:
: 
.
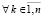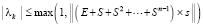Для нормы матрицы, согласованной с выбранной нормой вектора,
: 
.
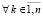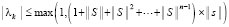Суммирование геометрической прогрессии влечет
: 
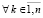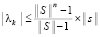, (33)
где S и s из (28). Очевидно, сумма модулей элементов любого столбца матрицы S не больше суммы модулей элементов первого столбца. Поэтому с учетом выбора норм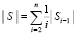 
. Поскольку 
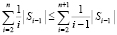, или 
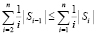, то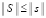 
. Подстановка в (33) влечет
: 
, 
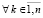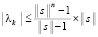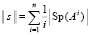. (34)
Теорема 2. Все собственные значения матрицы A оцениваются через следы ее степеней из (34),или
: 
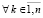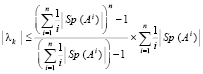. (35)
На практике проще (32), но (33)–(35) содержат выражение границ собственных чисел матрицы через функции ее элементов. Эти оценки удобны при применении метода Леверье, для произвольного полинома целесообразно применять (26).
Идентификация экстремумов функций двух действительных переменных
Чтобы найти все локальные минимумы функции двух действительных переменных в прямоугольнике на декартовой плоскости
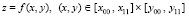, (36)
можно воспользоваться программой поиска нулей (как минимумов модуля) этой функции со следующими изменениями. Во-первых, функция function func (var x,y: extended): extended; определяется не по абсолютной величине, а непосредственно в виде (36) в программной форме. Во-вторых, радиус локализации определяется расстоянием не между ближайшими нулями в проекции на оси координат, а задается меньше половины расстояния между проекциями на оси координат ближайших друг к другу точек минимумов. В-третьих, необходимо снять ограничение на близость к нулю значения функции в идентифицированной точке минимума. Больше ничего в программе менять не нужно.
Пример 5. Пусть требуется найти все локальные минимумы функции
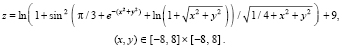(37)
Для решения используется программа (заданный в разделе констант полином будет использован в дальнейшем – для функции (37) он не нужен):
PROGRAM MINFuncXY;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n00=1024; np1=10;
type vect3=array [1..np1] of extended;
const b: vect3 = (-4.1,4.21,-2.1,-2,-2.221,0.102,0.203,-77,55.01,55.1);
b1: vect3 = (-44.33,-4,2,2.202,-5,-5.1,55.001,55.1,2.101,44.135);
type vect1=array [1..4*n00] of extended; vect2=array [1..4*n00] of longint;
var i,ii,j,k,kk,k1,r,ee,ee1,tty,nn0,mm: longint; c,a1,rex,imy: vect1;e,e3,e33: vect2;
aaa,x,x0,xk,xk0,xk1,hx,hy,min,eps1,eps11,eps12,eps13,z,z1,bbb,
y,y0,yk,yk0,yk1,ykk0,hh,yz,yz1,x00,x11,y00,y11,eps0,h,eps00,eps:extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
{процедура sort без изменений скопирована из программы FUNCPOLINOMutochnenie (korkompmin
примера 1)}
procedure identif1(var eps,x00,x11,y00,y11,eps0,h,x,yk0:extended;
var rex,imy: vect1;var kk:longint;var mm:longint);
label 21,22,23;
function func (x,y:extended):extended;
var p: extended; i1: integer;
begin
{p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1]));func:=abs(p)+33; end;}
func:=ln(1+sqr(sin((pi/3+exp(-(sqr(x)+sqr(y)))+ln(1+sqrt((sqr(x)+sqr(y)))))/sqrt(1/4+sqr(x)+sqr(y)))))+9;
{func:= ((sqr(y)+sqr(sqr(x)))-exp(-sqrt(x*x+y*y)));}
end;
procedure minx (var x,y,min:extended;var ee:integer);
begin
min:=func(x,y); ee:=0; for i:=1 to mm do begin x:=xk0+i*hx;
if min > func(x,y) then begin min:=func(x,y);ee:=i end end
end;
procedure miny (var x,y,min:extended;var ee1:integer);
begin
min:=func(x,y); ee1:=0; for i:=1 to tty do begin y:=ykk0+i*hy;
if min > func(x,y) then begin min:=func(x,y);ee1:=i end end
end;
procedure spuskx( var eps1, xk0,xk1,hx,y: extended);
begin
while abs(eps1) > eps do begin x:=xk0; minx (x,y,min,ee); eps1:=eps1/1.2;
xk0:=xk0+ee*hx-eps1;xk1:=xk0+eps1;hx:=abs(2*eps1)/mm end
end;
procedure spusky(var eps11,yk0,yk1,hy,x: extended);
begin
while abs(eps11) > eps do begin ykk0:=yk0; y:=yk0; tty:=mm;
miny (x,y,min,ee1); eps11:=eps11/1.2; yk0:=yk0+ee1*hy-eps11; yk1:=yk0+eps11;
hy:=abs(2*eps11)/mm end
end;
begin
aaa:=1e62;bbb:=1e62;kk:=0; x0:=x00; y0:=y00; nn0:=n00; hh:=nn0*h;
while x0 <= x11+hh do begin while y0 <= y11+hh do begin
for r:=1 to nn0 do begin x:=x0+r*h; ykk0:=y0; y:=y0; tty:=n00;hy:=h; miny (x,y,min,ee1); a1[r]:=min end;
sort( nn0, a1, e3); k:=1; while k<= nn0 do begin
for r := 1 to k-1 do if abs(e3[k]-e3[k-r]) <=eps0/h then goto 23; xk:= x0+e3[k]*h;
for r:=1 to nn0 do begin y:=y0+r*h; a1[r]:=func(xk,y) end;
sort( nn0, a1, e33); k1:=1; while k1<= nn0 do begin
for r := 1 to k1-1 do if abs(e33[k1]-e33[k1-r])<=eps0/h then goto 22; yk:= y0+e33[k1]*h; eps1:=eps0;
eps11:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; hx:=abs(2*eps1)/mm; y:=yk; spuskx(eps1,xk0,xk1,hx,y);
yk0:=yk-eps11; yk1:=yk+eps11; hy:=abs(2*eps11)/mm; x:=xk0+ee*hx+eps1; spusky(eps11,yk0,yk1,hy,x);
eps12:=eps0/1.2; xk0:=x-eps12; xk1:=x+eps12; hx:=abs(2*eps12)/mm; y:=yk0+ee1*hy+eps11;
spuskx(eps12,xk0,xk1,hx,y); eps13:=eps0/1.2; yk0:=yk0+ee1*hy-eps13; yk1:=yk0+2*eps13;
hy:=abs(2*eps13)/mm;
x:=xk0+ee*hx+eps12; spusky( eps13,yk0,yk1,hy,x); if func(xk,yk)= 0 then begin x:=xk; yk0:=yk; goto 21 end;
for i:= 1 to 2 do begin z:=x+i*h; if func(x,yk0) >= func(z,yk0) then goto 23; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x,yk0) >= func(z1,yk0) then goto 23; end;
for i:= 1 to 2 do begin yz:=yk0+i*h; if func(x,yk0) >= func(x,yz) then goto 22; end;
for i:= 1 to 2 do begin yz1:=yk0-i*h; if func(x,yk0) >= func(x,yz1) then goto 22; end;
if abs(aaa-x)<=1e-50 then goto 23; if abs(bbb-yk0)<=1e-50 then goto 22;
21: kk:=kk+1; rex[kk]:=x; imy[kk]:=yk0;
writeln (' ', x:2:30,' '); writeln (' ', yk0:2:30,' ',' ', func(x,yk0):2:30); writeln; aaa:=x; bbb:=yk0;
22: k1:=k1+1 end;
23: k:=k+1 end; y0:=y0+hh end; x0:=x0+hh; y0:=y00 end;
end;
begin
eps:=1e-44; mm:=4; x00:=-8; x11:=8; y00:=-8; y11:=8; eps0:= 0.49; h:=eps0/43; eps00:= eps0;
writeln; writeln (' ','Приближения экстремумов',' ');writeln;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm);
writeln; writeln (' ', 'Уточнения экстремумов',' '); writeln ;
eps0:= eps00/10; h:=eps0/43;
for ii:= 1 to kk do begin x00:=rex[ii]- eps00;x11:=rex[ii]+ eps00; y00:=imy[ii]- eps00;y11:=imy[ii]+ eps00;
identif1(eps,x00,x11,y00,y11,eps0,h,x,yk0,rex,imy,kk,mm); end;
readln;
end.
Результат работы программы:
Точки минимумов Точки минимумов
-0.058038369771222210000000000000 -0.000…00110000000000000
0.500930230856951840000000000000 9.00…00 -0.000…00000000000000000 9.509401122491339800…00
-0.293922087792833630000000000000 0.0889623215987226700…00
0.409767439970042010000000000000 9.00…00 0.4963720921726619700…00 9.00…00
…………………………………………………………………………………………
-0.319059901758565450000000000000 -0.000…00000000000000000
0.390512903297592400000000000000 9.00…00 -0.000…00000000000000000 9.5094011224913396800…00
0.024731117428831250000000000000 0.319079633792879890000000000000
-0.503674419450610690000000000000 9.00…00 0.390496780845504340000000000000 9.00…00
……………………………………………………………………………………………..
0.382875263535224740000000000000
0.328186046511627900000000000000 9.00…00
В рассматриваемом случае количество обнаруживаемых локальных минимумов зависит от радиуса локализации. В случае если число минимумов от этого не зависит, программа идентифицирует те и только те минимумы, которые функция имеет.
Пример 6. Пусть требуется найти все локальные минимумы функции
, 
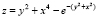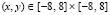. (38)
Для функции (38), заданной в виде func:= ((sqr(y)+sqr(sqr(x)))-exp(-sqrt(x*x+y*y))); та же программа даст результат:
Точка минимума
-0.000000000000000000000000000000
-0.000000000000000000000000000000 -1.000000000000000000000000000000
Дифференцируемость функции не требуется. Так, если взять полином из раздела констант по абсолютной величине, рассматривая его модуль как функцию двух переменных, и прибавить к нему число 33, p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func:=abs(p)+33; то результатом работы программы при соответственных параметрах
eps:=1e-44; mm:=4; x00:=-100; x11:=100; y00:=-100; y11:=100; eps0:= 0.49; h:=eps0/43;eps00:= eps0;
будет значение abs(p)+33, достигаемое в корнях исходного полинома:
Точки минимумов Точки минимумов
-77.0000…0000 -4.1000…0000
55.1000…0000 33.00…00 -44.3300…0000 33.00…00
0.1020…0000 -2.1000…0000
-5.1000…0000 33.00…00 2.0000…0000 33.00…00
-2.0000…0000 -2.2210…0000
2.2020…0000 33.00…00 -5.0000…0000 33.00…00
4.2100…0000 0.2030…0000
-4.0000…0000 33.00…00 55.0010…0000 33.00…00
55.0100…0000 55.1000…0000
2.1010…0000 33.00…00 44.1350…0000 33.00…00
Замечание 6. В отличие от поиска корней полинома или нулей функций в рассматриваемой программе не остается условий фильтрации неточных приближений. Однако это можно сделать по мере близости точек минимума, выбирая точки с наименьшим в них значением функции.
Максимумы идентифицируются по этой же программе, если на входе задать функцию с обратным знаком, найти ее минимумы, затем на выходе поменять знак на исходный. Можно поступить иначе, применив непосредственно условие максимума. В этом случае необходимо изменить знак неравенства на противоположный в процедурах минимизации, а также на границах текущего прямоугольника. Рассматриваемые операторы примут вид:
k:=1; while k<= nn0 do begin
for r := 1 to nn0-k do if abs(e3[k]-e3[k+r]) <=eps0/h then goto 23; xk:= x0+e3[k]*h;
k1:=1; while k1<= nn0 do begin
for r := 1 to nn0-k1 do if abs(e33[k1]-e33[k1+r])<=eps0/h then goto 22; yk:= y0+e33[k1]*h;
procedure minx (var x,y,min:extended;var ee:integer);
begin
min:=func(x,y); ee:=0; for i:=1 to mm do begin x:=xk0+i*hx; if min < func(x,y) then begin min:=func(x,y);
ee:=i end end end;
procedure miny (var x,y,min:extended;var ee1:integer);
begin
min:=func(x,y); ee1:=0; for i:=1 to tty do begin y:=ykk0+i*hy; if min < func(x,y) then begin min:=func(x,y);
ee1:=i end end end;
for i:= 1 to 2 do begin z:=x+i*h; if func(x,yk0) < func(z,yk0) then goto 23; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x,yk0) < func(z1,yk0) then goto 23; end;
for i:= 1 to 2 do begin yz:=yk0+i*h; if func(x,yk0) < func(x,yz) then goto 22; end;
for i:= 1 to 2 do begin yz1:=yk0-i*h; if func(x,yk0) < func(x,yz1) then goto 22; end;
Так, если эти преобразования применить к той же программе MINFuncXY и на входе задать значение полинома с обратным знаком
p:=1; for i1:=1 to np1 do p:=p*(sqr(x-b[i1])+sqr(y-b1[i1])); func:=-abs(p);
то результатом программы будут все корни полинома, найденные как максимумы модуля с минусом (для корней можно воспользоваться фильтрацией по величине модуля полинома).
Заключение
Изложен компьютерный метод инвариантной идентификации экстремумов функций двух действительных переменных и нулей функций одной комплексной переменной на основе устойчивой адресной сортировки. Инвариантность относится к виду входной функции, к области поиска одновременно всех нулей и экстремумов без их априорной локализации. Поиск нулей функции комплексной переменной сводится к случаю функции двух действительных переменных умножением на комплексно сопряженное значение. На этой основе выполняется поиск корней полиномов от одной комплексной переменной с комплексными коэффициентами, корней характеристического полинома матрицы с учетом кратности. Для линейной дифференциальной системы с матрицей постоянных коэффициентов идентифицированные корни определяют характер устойчивости в смысле Ляпунова. Метод реализован программно, на основе сортировки вычислительные операции заменяются операциями сравнения, в результате достигается точность приближения нулей и экстремумов без потери значащих цифр в формате представления данных. Программа за приемлемое время выполняется на персональном компьютере, дано преобразование метода к параллельной форме. Безусловная численная оптимизация выполняется без априорного указания области, структуры расположения нулей и экстремумов, без локализации начальных приближений. Приводятся оценки области корней полиномов и характеристических чисел матрицы. Построение программ переносится на случай функций нескольких переменных [15].
Библиографическая ссылка
Ромм Я.Е. ИДЕНТИФИКАЦИЯ НУЛЕЙ И ЭКСТРЕМУМОВ ФУНКЦИЙ НА ОСНОВЕ СОРТИРОВКИ С ПРИЛОЖЕНИЕМ К АНАЛИЗУ УСТОЙЧИВОСТИ. II. СЛУЧАЙ ДВУХ ДЕЙСТВИТЕЛЬНЫХ И ОДНОЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ // Современные наукоемкие технологии. – 2020. – № 6-2. – С. 254-282;URL: https://top-technologies.ru/ru/article/view?id=38101 (дата обращения: 19.04.2024).