Задачи оптимизации распространены во многих сферах, таких как медицина, металлургия, логистика и др. Получение оптимальных параметров позволяет добиться существенных преимуществ, что эффективно сказывается на предприятии в условиях сильной конкуренции. Не является исключением и задача оптимального использования ресурсов, которая позволяет не только сократить количество отходов, но и повысить количество выпускаемой продукции. Одной из таких сфер является металлургия, особый интерес представляет обработка цветных и драгоценных металлов. Неэффективное использование таких материалов влечет безвозвратные потери материала и увеличение затрат на переработку отходов. Часто подобные производства могут быть реализованы следующим образом. Детали разной формы изготавливаются из одного слитка путем его деформации. Исходный слиток прямоугольной формы прокатывается до определенной толщины, затем из него вырезаются заготовки. Такая процедура повторяется до тех пор, пока детали могут быть размещены. Стоит отметить, что для экономии материала резка осуществляется на гильотине. Одна из проблем, связанных с таким способом производства, заключается в планировании. Детали большей толщины располагаются на листе в первую очередь. Таким образом, вероятность размещения более тонких деталей уменьшается. Однако их приоритет может быть выше прочих. В большинстве случаев человеку не под силу учесть это при изготовлении деталей.
В результате эта задача является одной из разновидностей известной задачи упаковки прямоугольников (BPP). BPP – это задача оптимизации, которая минимизирует количество отходов или используемых ресурсов. BPP имеет большое количество разновидностей. Так, наиболее известными являются варианты с наличием гильотинных ограничений, фиксированной или неограниченной длиной листа, возможностью поворота деталей [1]. Использование дополнительных ограничений приводит к появлению новых вариантов задачи. В этой работе рассматривается задача приоритетной упаковки (P) в несколько контейнеров неизвестной ограниченной длины (M) с несовместимыми категориями (IC) и гильотинными ограничениями (G). Мы закодируем эту задачу как BPP|P|M|IC|G.
Учет приоритетов в BPP|P|M|IC|G позволяет размещать приоритетные элементы в первую очередь, что дает возможность соблюдать порядок производства. Несовместимость групп деталей вытекает из их геометрических размеров, а именно из толщины. Детали разной толщины не могут быть размещены в одном контейнере. Стоит отметить, что оптимальное количество контейнеров, на которые необходимо разбить исходный контейнер, заранее не известно, как не известна и их длина. В результате в качестве решения задачи необходимо не только предоставлять схему упаковки, но и вычислить оптимальное разбиение исходного контейнера на несколько частей.
Для решения BPP|P|M|IC|G предлагается новая метаэвристика. Она основывается на применении приоритетной эвристики, предложенной в [2], с несколькими модификациями. Предлагаемый алгоритм тестируется на наборах прямоугольников, специально составленных для этой задачи.
Целями данного исследования являются получение математической формулировки задачи приоритетной упаковки с несовместимыми категориями и динамически изменяемыми размерами контейнеров, а также разработка алгоритма ее решения.
Стоит отметить, что задача BPP является NP-полной. Это означает, что не существует алгоритмов, решающих эту задачу за полиномиальное время. Таким образом, необходимо разрабатывать эвристические алгоритмы, которые позволяют получить приближенное решение за приемлемое время работы.
Задача упаковки прямоугольников (BPP) хорошо изучена и описана в различных источниках (например, [3]). Существует также множество вариаций этой задачи. В контексте нашей постановки рассмотрим несколько вариаций наиболее близких задач. Одним из вариантов задачи упаковки является задача с учетом приоритета (2DBPP|D), которая называется задачей дуальной, или приоритетной, упаковки. В литературе уделяют мало внимания приоритетности изготовления деталей в промышленности и в большей степени склоняются к физическим и ценовым характеристикам элементов. Поэтому неудивительно, что эта вариация получила свое развитие в сфере медицины для оптимальной загрузки медицинского оборудования. Проблема приоритетной упаковки рассматривается в работах [4, 5], где ставится задача распределения ресурсов с учетом ограниченного времени проведения операции. Дальнейшее развитие она получила в работе [6], где была описана математическая модель задачи планирования и приводилось ее решение с помощью эвристики на основе алгоритма First Fit Decreasing.
Другим вариантом задачи 2DBPP является упаковка в несколько полос (2DMBPP). Эта задача имеет два варианта постановки: с одинаковыми и с переменными размерами контейнеров (2DVSBPP). Эта задача встречается при оптимизации нагрузки на вычислительные ресурсы, в логистике и т.д. Так, в работе [7] предлагается ряд эвристических методов и рассматривается их приложение для решения задачи логистики как обобщенной задачи упаковки контейнеров с прибылями, зависящими от контейнера. Применение 2DMBPP для пакетного планирования с распределением ресурсов было рассмотрено в [8], где эвристика использовалась для минимизации потребления ресурсов. Исследование алгоритма First Fit для задачи упаковки с ограничением по количеству элементов проводилось в работе [9]. В основном авторы рассматривают упаковку в контейнеры фиксированного или разного размера. Никаких ограничений по динамически изменяющимся размерам или по неопределенному количеству контейнеров не ставится.
Задача упаковки с конфликтами (BPC) рассматривает возможность несовместимости отдельных элементов. Часто в таких задачах для определения совместимости между элементами используется граф, где вершины обозначают элементы или группы, которые должны быть упакованы, а ребра – совместимость между ними. Например, в работе [10] рассматривается решение задачи с помощью эвристических методов на основе древесной декомпозиции. Алгоритм разбивает задачу на подзадачи, которые решаются независимо. Затем происходит объединение полученных решений. В работе [11] авторы приводят обновленные верхние и нижние границы для BPC, а также детерминированный алгоритм на основе формулировки покрытия множества, решаемый с помощью алгоритма ветвления и цены.
В последнее время появилась новая задача упаковки с совместимыми категориями (BPCC) [12]. Она является обобщением задачи упаковки с конфликтами (BPC), где рассматривается попарная несовместимость. BPCC предполагает совместимость отдельных групп упаковываемых элементов. В работе [12] впервые ставится задача BPCC. Авторы приводят модификацию алгоритма поиска переменной окрестности (VNS), а также предлагают набор тестовых примеров, на котором проводят обширное тестирование алгоритма.
Таким образом, приведенные здесь задачи упаковки так или иначе схожи с предлагаемой нами формулировкой задачи. Однако ни одна из предложенных задач не рассматривает случай с не известным заранее количеством контейнеров и их динамически изменяющимися размерами. Кроме этого, насколько нам известно, это первое рассмотрение задачи с совокупностью ограничений, таких как гильотинные разрезы, наличие приоритетов и несовместимые группы прямоугольников.
Постановка задачи
Обычная BPP заключается в размещении набора прямоугольников R = {ri, i = 1, ..., n} с размерами ri = (wi, li), где wi – ширина, li – длина i-го прямоугольника. Прямоугольники размещаются на листе фиксированного размера с шириной W0 и длиной L0 без перекрытия. Целевой функцией в данном случае является площадь отходов:
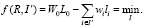(1)
Здесь I` – множество индексов размещенных прямоугольников, I` ⊆ I = {i = 1, ..., n}.
Для постановки задачи BPP|P|M|IC|G представим прямоугольник в виде ri = (wi, li, hi, pi). Здесь hi ∈ H = {hj, j ∈ I} – толщина i-го прямоугольника. Толщина прямоугольника задает толщину листа, из которого он может быть изготовлен. Например, на листе толщиной 2 мм могут быть размещены прямоугольники с соответствующей толщиной. Лист постепенно деформируют (прокатывают) до определенной толщины, изготавливают детали, и оставшийся лист деформируют повторно. Это делает невозможным одновременное размещение прямоугольников разной толщины. Использование толщины позволяет сгруппировать прямоугольники в m = |supp H| групп. При этом:
, 
,
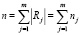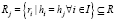где hj – толщина группы прямоугольников, j ∈ J = {1, ..., m} и Hj = {nj · hi | hi = hj ∀i ∈ I }. Эти группы являются несовместимыми.
Приоритет i-го прямоугольника pi ∈ P = = {pi, i ∈ I | pi ∈ Ζ >0} характеризует степень важности для производства. Чем больше pi, тем предпочтительнее деталь для размещения на текущем листе. В случае одинакового приоритета порядок размещения прямоугольников не важен. Мы примем pi = 1 как максимальный приоритет, т.е., чем выше значение pi, тем ниже приоритет. Прямоугольники в каждой группе Hj (j = 1, ..., m) можно сгруппировать в qj = |supp Pj| подгрупп, где Pj = {pi, i ∈ Ij ⊆ I}⊆ P. При этом:
, 
,
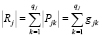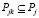где Pjk = {gjk • pi | pi = pjk ∀ i ∈ Ijk ⊆ I}, а Ijk – индексы прямоугольников с одинаковым приоритетом в группе Rj. Стоит отметить, что при pi = const, ∀i ∈ I задача BPP|P|M|IC|G вырождается в BPP|M|IC|G, т.е. без учета приоритета.
Мы полагаем, что при деформации листа (прокатке) его размеры изменяются по правилу сохранения объема, т.е. V0 = V1, где V0 = W0L0h0 – объем до деформации, V1 = W1L1h1 – объем после деформации. Пренебрегая изменениями размеров одной из сторон листа, ортогонально которой происходит деформация (например, W0), получаем:
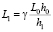, γ > 0, (2)
где γ – коэффициент для учета дефектов, возникающих на концах листа при деформации. Далее для простоты принимается γ = 1.
Таким образом, BPP|P|M|IC|G заключается в размещении прямоугольников с учетом приоритета и разбиении исходного контейнера на субконтейнеры с учетом динамически изменяющейся длины. Как упоминается в работе [13], задачу (1) с учетом приоритета можно представить в виде задачи многокритериальной оптимизации:
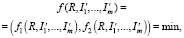(3)
,
,
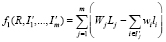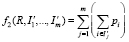где I`j – множество индексов размещенных прямоугольников группы Rj. Если I`j = ∅, то прямоугольники из группы Rj не были размещены. Размеры контейнера (Wj, Lj), выделенного для упаковки прямоугольников группы Rj, должны определяться исходя из правила деформации (2) и конфигурации соответствующей группы. При этом если I`j = ∅, то WjLj = 0.
Накладывая дополнительные ограничения на задачу (3), можно получать различные вариации задачи упаковки:
– стороны прямоугольников должны быть параллельны сторонам листа;
– прямоугольники разрешено поворачивать на 90 градусов (R);
– все разрезы должны быть только гильотинными (G);
– деформация листа производится в фиксированном направлении (FD) (например, вдоль L0).
В данной работе мы рассматриваем задачу гильотинной приоритетной упаковки прямоугольников с несовместимыми категориями и фиксированным направлением деформации BPP|P|M|IC|G|FD.
Приоритетная эвристика
Приоритетная эвристика (PH) – это однопроходная детерминированная эвристика, предложенная в [2]. Она представляет собой рекурсивную процедуру упаковки для обеспечения гильотинных ограничений. Выбор прямоугольника из набора осуществляется с помощью «внутренних» приоритетов, характеризующих один из пяти возможных вариантов размещения. Таким образом, прямоугольник с большим приоритетом выбирается первым. Алгоритм имеет один параметр для настройки, а именно вариант сортировки: по длине или по ширине. В своей работе авторы проводят результаты работы алгоритма на разных примерах из литературы, в том числе на основе дата сета ZDF, предложенного в [14, 15]. В результате отмечается, что PH хорошо подходит для крупномасштабных задач.
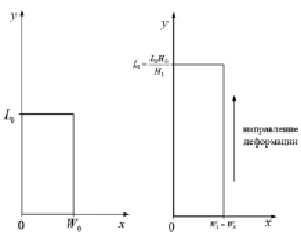
Рис. 1. Положение исходного контейнера и направление его деформации
Для соответствия BPP|P|M|IC|G в PH были внесены некоторые изменения. Так, сортировка прямоугольников выполняется в каждой группе Rjk отдельно. В алгоритм упаковки добавлен параметр сдвига по оси Y. Это позволяет последовательно упаковывать группы прямоугольников, сохраняя их положение.
Для учета приоритетности прямоугольников в алгоритме упаковки деталей с RG итерации проводятся только по элементам наивысшего приоритета p. При этом в процедуре рекурсивной упаковки RecursivePacking(x, y, w, h) этап оценки внутреннего приоритета проводится в порядке убывания приоритета (по подгруппам Rjk) всей группы элементов Rj с одной толщиной. Это позволяет заполнять пространство, в котором невозможно разместить прямоугольники высокого приоритета, прямоугольниками более низкого приоритета.
Последовательный метаэвристический алгоритм
Примем такое расположение исходного контейнера, что его горизонтальная сторона соответствует ширине W, а вертикальная соответствует длине L (рис. 1). Пусть деформация (прокатка) происходит вдоль L, а W остается постоянной.
Одна из задач алгоритма – распределить длины субконтейнеров для прямоугольников из групп Hj, j ∈ J. Очевидно, что длина каждого субконтейнера лежит в пределах L0 ≤ L ≤ L0h0/min H, где h0 ≥ min H толщина исходного контейнера. Таким образом, одним из результатов работы алгоритма должно стать отображение Lbins: supp H → R+, которое ставит в соответствие толщине упакованной группы длину субконтейнера, на которые будет разбит исходный контейнер с учетом его деформации. Последовательность всех длин субконтейнеров должна удовлетворять неравенству:
.
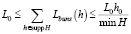Стоит отметить, что, чем больше выделен размер контейнера для группы с одной толщиной, тем меньше места остается для упаковки остальных групп. Это необходимо учитывать при распределении длин. Другими словами, упаковка прямоугольников группы Rj оставляет меньше шансов на то, что все прямоугольники первого приоритета группы Ri (i ≠ j) будут упакованы.
Предлагаемая последовательная метаэвристика (SM) рассматривает подгруппы прямоугольников Rjk в порядке их следования в отсортированной последовательности G = {(hj, pjk), k = 1, ..., qj, j = 1, ..., m}. Сортировка осуществляется лексикографически по неубыванию приоритета и невозрастанию толщины. Это позволяет упаковывать прямоугольники большей толщины в первую очередь. Использование pjk позволяет учесть приоритетность упаковки деталей. Благодаря такому упорядочиванию подгруппы Rjk с высоким приоритетом упаковываются в первую очередь, затем оставшееся место распределяется между подгруппами в порядке увеличения pjk.
Итеративная процедура алгоритма (рис. 2) построена следующим образом. Контейнер деформируется до толщины группы деталей Rj по правилу (2), после чего упаковка осуществляется с помощью алгоритма PH. Результатом упаковки выступают необходимая длина контейнера L` и мультимножество прямоугольников R`j. В завершение итоговое решение обновляется, длина и толщина исходного контейнера корректируются. Стоит отметить, что в отсортированной последовательности G элементы hj не обязательно будут упорядочены в порядке невозрастания. Это происходит потому, что значения pjk имеют приоритет над hj. Поэтому в процессе поиска решения длина контейнера может как увеличиваться (h0 > h1 в (2)), так и уменьшаться (h1 > h0 в (2)). Это приводит к неупорядоченной упаковке относительно hj. Однако в процессе производства лист прокатывается в порядке убывания толщины. Поэтому по завершении процедуры необходимо отсортировать группы размещенных прямоугольников в нужном порядке.
Во время упаковки могут возникнуть два случая. Первый заключается в том, что все прямоугольники подгруппы Rjk могут быть размещены в контейнер текущей длины, а оставшееся место будет отведено для упаковки других подгрупп. Тогда необходимо воспользоваться алгоритмом для задачи упаковки в полосу, который, помимо схемы размещения, возвращает необходимую длину. За это отвечает процедура PackStrip(W, Rj, yc), где yc отвечает за сдвиг координат схемы размещения по оси Y. Второй случай возникает, когда длины контейнера не хватает для размещения всех прямоугольников подгруппы Rjk. Тогда необходимо явно задать его длину и воспользоваться вариантом алгоритма для задачи упаковки контейнера, который представлен процедурой PackBin(W, ¯L, Rj, yc), где ¯L – оставшаяся длина контейнера. В качестве этих процедур у нас выступает алгоритм PH для SPP и BPP. Необходимо отметить, что можно использовать и другие эвристики для решения этих задач. Ограничения накладываются только на вариант решаемой задачи (SPP и BPP). Не ограничивается применение разных эвристик с целью получения оптимального плана раскроя. Кроме того, свойства используемых алгоритмов сохраняются, например, если эвристика предназначена для решения задачи с фиксированной ориентацией прямоугольников (SPP|O, BPP|O) или с возможностью их поворота (SPP|R, BPP|R), и SM также будет решать этот вариант задачи. Это позволяет обеспечить широкий круг решаемых задач и вариативность свойств за счет выбора базовых эвристик.
Несмотря на порядок приоритетов в последовательности G, в процедуры упаковки передаются не подгруппы Rjk, а группы Rj. Это делается для того, чтобы обеспечить заполнение пустого пространства прямоугольниками более низкого приоритета в том случае, если ни один прямоугольник соответствующего приоритета p не может быть упакован. В связи с этим необходима проверка мультимножества Rjk на пустоту, поскольку все его элементы могут быть упакованы ранее.
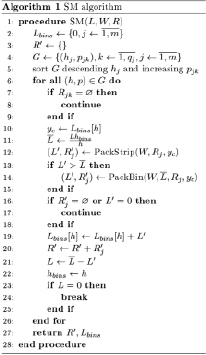
Рис. 2. Алгоритм SM
SM может «дробить» одну группу Rj на несколько частей и упаковывать их по отдельности. Несмотря на это, обеспечивается последовательность схемы раскроя каждой группы.
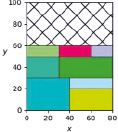
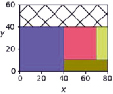
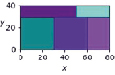
Наглядная демонстрация работы алгоритма приводится на рис. 3. Здесь видно, что размеры незаполненной части контейнера преобразуются с помощью (2) и выступают в качестве контейнера для упаковки более тонких прямоугольников.
Результаты исследования и их обсуждение
Последовательный метаэвристический (SM) алгоритм с использованием приоритетной эвристики (PH) был протестирован на 10 примерах, составленных специально для задачи BPP|P|M|IC|G. Примеры содержат от 3 до 14 несовместимых категорий и от 3 до 5 приоритетов. Примеры составлены таким образом, чтобы включать задачи с числом элементов из широкого диапазона. Так, наборы 1, 8 и 10 содержат относительно немного элементов (n < 1000), а крупномасштабные наборы 6 и 7 включают более 10 000 элементов.
Для возможности сопоставимости результатов работы алгоритма оценка качества упаковки каждой группы проводится аналогично [2] с помощью показателя Gapj = 100(Lj – Lj*) / Lj*, где Lj* – известная оптимальная длина контейнера или нижняя граница (LB), а Lj – длина контейнера, полученная с помощью SM, j = 1, ..., m. При этом длина контейнера не ограничивается, т.е. решается SPP. Результирующий показатель определяется как среднее взвешенное:
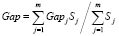, (4)
где Sj – площадь всех прямоугольников j-й группы. На рис. 3 представлены результаты работы SM на SPP|P|M|IC|G. Из рис. 4 видно, что влияние метода сортировки алгоритма PH сохраняется.
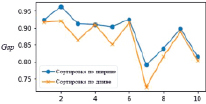
В случае BPP|P|M|IC|G размер контейнера ограничен, что, несомненно, приводит к ухудшению качества работы вследствие влияния приоритета прямоугольников. Показатель Gap (4) для BPP|P|M|IC|G представлен на рис. 5, a. Можно заметить, что в некоторых случаях Gap (4) становится отрицательным. Это происходит, когда длина контейнера, выделенная алгоритмом SM для какой-либо группы, меньше оптимальной, соответственно некоторые прямоугольники не могут быть упакованы. Существенное отклонение наблюдается для примера 10.
а) б) в)
Рис. 3. Упаковка прямоугольников толщиной 3 мм (a), 2 мм (б) и 1 мм (в) на исходный лист с размерами L0 = 100, W0 = 80, H0 = 3
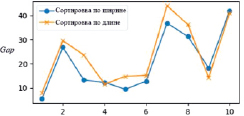
Рис. 4. Результаты работы SM с PH при разных методах сортировки на SPP|P|M|IC|G
Он содержит несколько низкоприоритетных прямоугольников больших размеров. Несмотря на это, плотность заполнения каждого контейнера высока. На рис. 5, б приведена средняя относительная площадь для каждого примера: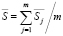
, 
.
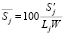Здесь ‾Sj – отношение площади размещенных прямоугольников к площади контейнера, где S`j – площадь размещенных прямоугольников, а Lj – длина контейнера. На рис. 5, a и б можно видеть, что метод сортировки по длине показывает результат хуже относительно сортировки по ширине.
Выводы
В работе ставится новая задача приоритетной упаковки прямоугольников с несовместимыми категориями и динамически изменяющимися размера контейнеров (BPP|P|M|IC|G). Эта задача определяется тем, что размеры исходного контейнера изменяются в процессе упаковки, при этом необходимо учитывать приоритетность деталей, их несовместимость между собой и гильотинные ограничения. Для решения представленной задачи предлагается новый последовательный метаэвристический алгоритм (SM), который в процессе работы разделяет группы прямоугольников по их приоритетам и категориям. Полученные группы размещаются последовательно, при этом остается возможность заполнения свободного пространства прямоугольниками более низкого уровня. В качестве базового алгоритма используется однопроходной детерминированный эвристический алгоритм PH, показывающий хорошие результаты среди аналогов. Но SM не ограничивается рассмотренной эвристикой. В качестве базового алгоритма можно использовать любые алгоритмы, позволяющие решать BPP и SPP. Свойства этих алгоритмов сохраняются. Так, в приведенных примерах показано, что при использовании PH его зависимость от варианта сортировки унаследована SM. Стоит отметить гибкость SM относительно выбираемых алгоритмов. Их можно комбинировать для достижения необходимых свойств.
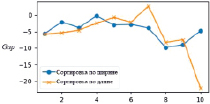
a) б)
Рис. 5. Результаты работы SM с PH при разных методах сортировки на SPP|P|M|IC|G
Качество работы SM было продемонстрировано на наборе примеров. Наборы различаются как количеством элементов, так и их распределением по категориям и приоритетам. При решении BPP|P|M|IC|G и SPP|P|M|IC|G алгоритм показывает хорошие результаты, а свойства решения зависят от свойств используемого базового алгоритма.
Поскольку, как нам известно, это первое исследование BPP|P|M|IC|G, может быть много возможных вариантов дальнейшего развития. Так, остается открытым вопрос о возможности изменения направления деформации контейнера. Возможности применения стохастических и детерминированных алгоритмов локальной и глобальной оптимизации и их комбинаций также широки. Одним из вариантов является распределение длин субконтейнеров с помощью глобальной оптимизации.
Библиографическая ссылка
Воронов В.С., Пересунько П.В., Виденин С.А., Матюхин Н.Е. ПОСЛЕДОВАТЕЛЬНАЯ МЕТАЭВРИСТИКА ДЛЯ ЗАДАЧИ ПРИОРИТЕТНОЙ УПАКОВКИ С НЕСОВМЕСТИМЫМИ КАТЕГОРИЯМИ // Современные наукоемкие технологии. – 2020. – № 6-2. – С. 220-227;URL: https://top-technologies.ru/ru/article/view?id=38096 (дата обращения: 23.11.2024).