В настоящее время наблюдается повышенный интерес к задаче распознавания образов в различных приложениях. Актуальность данного научного направления подтверждается большим числом разнообразных методов и подходов, опирающихся в том числе на искусственные нейронные сети, марковские модели, анализ главных компонент, анализ вейвлетов, метод опорных векторов и др. инструменты. Высокие результаты в сфере обработки графической информации и распознавания образов в ней получены как отечественными, так и зарубежными авторами (В.А. Сойфер, Ю.И. Журавлев, П.А. Бакут, Я.А. Фурман, I.E. Sobel, L.G. Roberts, W.K. Pratt и др.).
У графических образов есть характеристики, не зависящие, например, от уровня освещения, контраста, гаммы, угла поворота, общего качества изображения. Эти характеристики – инварианты. В работах А.А. Шмидта, С.И. Аверина, Е.П. Путятина, B. Zitova, T. Suk, J. Flusser, R. Dib, F. Baker, N. Zaeri, E.L. Hall, R.Y. Wong, M.K. Hu выполнена систематизация знаний об использовании инвариантов в сфере обработки графических данных и классификации. Следует отметить, что задача качественного распознавания в настоящее время считается актуальной и нерешенной, так как известные подходы не дают приемлемых результатов при колебаниях освещения и всем многообразии возможных ракурсов съемки объектов различной природы. Например, в случае движения целевых объектов на видеопоследовательности из-за искажений и яркостных шумов имеет место низкая точность и полнота распознавания.
Исследование посвящено обзору методов распознавания образов. Выделяются особенности различных подходов к решению задачи распознавания образов, в том числе учитывающих свойства яркостных и геометрических инвариантов изображений.
Материалы и методы исследования
Основные понятия и определения
Здесь будем опираться частично на определения, содержащиеся в работе [1].
Инвариант – интегральный дескриптор изображений, отражающий их яркостные и/или геометрические параметры, обладающий устойчивостью к яркостным и/или аффинным преобразованиям. Функционал или дескриптор инварианта определяется так, что сохраняет свои значения при использовании допустимых преобразований, в том числе операторов, изменяющих вид изображения в худшую сторону, при этом значения функционала для разных изображений – разные.
Наиболее значимые – яркостные инварианты, устойчивые к мультипликативным и/или аддитивным вариациям яркости. Полезным инструментом может служить подход, связанный с выделением линий положения, не зависящих от смены освещенности [2].
Алгебраическим инвариантом назовем дескриптор изображения, построенный на основе степенных моментов, являющийся инвариантным к аффинным и/или иным преобразованиям. Примером служат инвариантные моменты Hu [3], эффективные как признаки при трекинге и классификации объектов с меняющейся ориентацией. Субинвариантными инвариантами назовем дескрипторы изображения, степень изменения которых при аффинных и/или яркостных преобразованиях находится в допустимых, фиксированных пределах, достаточных для качественной классификации целевых объектов. Практически все дескрипторы реальных изображений являются субинвариантами, поскольку чувствительны к изменениям внешней среды.
Анализ современного состояния исследований в предметной области
В решении задачи классификации важным этапом является выбор системы признаков / информативных параметров. Извлечение признаков, являющихся инвариантами, часто является эвристическим. Далее приведем анализ основных особенностей наиболее актуальных на сегодня методов для работы с образами.
Метод опорных векторов (Support Vector Machines, SVM) [4] применяется в задачах регрессионного анализа и при классификации. Метод основывается на выделении гиперплоскости в пространстве информативных признаков. Эта гиперплоскость должна разделить классы образов. Из недостатков отмечается необходимость значительных затрат времени при настройке классификатора, существенные объемы используемой оперативной памяти.
Алгоритм AdaBoost [5] эффективно применяется при поиске целевых объектов в потоках графической информации. Например, система поиска целевых объектов, опирающаяся на AdaBoost [6], показала свою эффективность по точности и скорости работы. В качестве признаков можно использовать, например, вейвлеты Хаара. Очевидным является использование методов снижения размерности пространства признаков. В качестве положительных качеств алгоритма можно указать высокую точность и наглядность математического аппарата. Недостаток – необходимость использования существенного объема обучающих примеров.
Скрытые марковские модели [7] опираются на пространственные особенности сигналов и их статистические характеристики. Модель включает подмножества скрытых и наблюдаемых состояний, матрицу переходных вероятностей и начальную вероятность состояний. При распознавании выполняется проверка того, что имеет место максимум вероятности, что ряд наблюдений за анализируемым объектом интереса сформирован определенной моделью. Однако метод требует подбора параметров модели для каждой обучающей выборки.
Метод линейного дискриминантного анализа (Linear Discriminant Analysis, LDA) [8] содержит этап проекции пространства целевых объектов на признаковое пространство. При этом выполняются условия минимизации/максимизации внутриклассовых и межклассовых расстояний в признаковом пространстве. Метод используется в задаче уменьшения размерности пространства признаков. Остается нераскрытым вопрос об использовании LDA при единовременном варьировании ракурса и освещенности изображений.
Рассмотрим далее некоторые публикации, в которых применялись различные инварианты.
Анализ контуров в методах обработки видеоданных с объектами известной формы эффективен ввиду того, что контур является самой информативной информацией о них. Мы можем делать аналитические описания контуров, не меняющиеся при сдвиге, повороте и изменении масштабов целевых объектов [9]. В работе [10] поиск инвариантов осуществляется на основе преобразований Хаффа. Следует указать на работу [11], ориентированную на обработку 3D-изображений, отметим, однако, малую исследованность 3D-распознавания целевых объектов. В статье [12] выполняется сопоставление графических образов путем поиска «критических» опорных точек перегиба, взаимопересечений, максимума кривизны и пр.
Большое внимание уделяется построению универсальных инвариантов, не требующих рассмотрения внутренней структуры изображения. В частности, этому условию удовлетворяют инварианты Hu. В работе [13] использовался информационный вектор 11 инвариантов, а в исследовании [14] рассмотрены свойства моментов Hu. Выявлено, что инвариантные моменты обладают существенно отличающейся чувствительностью к вариациям входных данных. Отметим работу [15], систематизирующую знания об использовании инвариантов. В работе [16] инвариантные моменты применялись для распознавания рукописных цифр.
Актуальной областью исследований, на наш взгляд, является распознавание с использованием комбинированных подходов. В том числе можно изучить методы совмещенного применения инвариантов и нейронных сетей в задачах распознавания объектов различной природы. Нейронные сети прямого распространения, вероятностные и сверточные нейронные сети эффективно работают с выделенными инвариантными дескрипторами. Нейросетевые классификаторы успешно апробированы в работе с данными телеметрии с датчиков космических аппаратов [17].
Научная идея заключается в разработке и исследовании яркостных и геометрических инвариантов как интегральных дескрипторов с целью построения на их основе эффективных алгоритмов распознавания образов в условиях яркостной и геометрической неустойчивости изображений. Подобная интеграция приводит к существенному снижению размерности признакового пространства при одновременном повышении качества распознавания в нестабильных условиях внешней среды [18].
Методы построения инвариантов как интегральных признаков для задачи распознавания
Будем исследовать яркостную функцию изображения как процесс, а именно – случайный и стационарный. В такой постановке задачи целевые признаки обрабатываемого изображения – числовые сведения о случайном процессе. Достаточно часто применяемые характеристики – нормализованная гистограмма распределения яркостных значений на изображении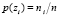 
, где ni – число пикселей яркости уровня zi 
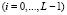, n – общее количество пикселей изображения, L – количество возможных значений яркости. Величина p(zi) – оценка вероятности обнаружения на снимке пикселя с яркостью zi, таким образом, выполняется условие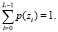 
В исследованиях [3, 19] предложены 7 инвариантов к аффинным преобразованиям. Легко проверяется, используя подстановки и преобразования, что инварианты Hu устойчивы к операциям сдвига и масштабирования. В работе [20] осуществлена проверка группы 2D-инвариантов. Работа подтвердила корректность формул инвариантных моментов, были подсчитаны уровни их устойчивости. Однако это верно лишь для неискаженных изображений. В реальности же объекты на снимках имеют разнообразные дефекты и подвержены тем или иным преобразованиям. Таким образом, в такой ситуации мы имеем дело с «псевдоинвариантами», чувствительными к шумам и искажениям формы объектов, что приводит к необходимости создания представительных обучающих выборок графических изображений. Нетрудно убедиться в том, что моменты для полутоновых объектов очень чувствительны к изменениям освещенности.
Определим центральные моменты изображения
,
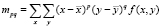где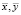 
– центр тяжести образа, моменты mpq – моменты порядка не выше 
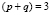, f(x, y) – яркостная функция растрового изображения. Качество исходных изображений прямым образом оказывает влияние на результаты классификации [21], по умолчанию считаем, что исходные данные превосходного качества, отсутствует необходимость в предобработке. Задача определения расстояний до наблюдаемого объекта с использованием моментов решается в работе [14].
Использование инвариантов для распознавания лиц для плоского случая было рассмотрено в работе [22], рассмотрим далее 3D-случай. Пусть ρ(x, y, z) – непрерывная 3D-функция яркости точек. Для успешного сопоставления 3D-образов необходимы инвариантные к аффинным преобразованиям моменты. С использованием работ [23–25] нами были отобраны следующие инварианты:
;
;
;
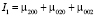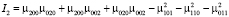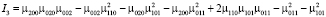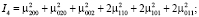
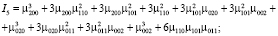
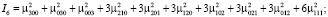
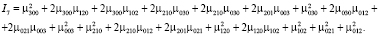
Данный набор 3D-инвариантов обеспечивает возможности для эффективного распознавания. Подход к решению оптимизационной задачи наведения 3D-моделей на 2D-изображения объектов рассмотрен в [26].
Комбинированные инварианты изображений
Существуют инварианты, нечувствительные к нарушениям фокуса средств технического зрения, атмосферным возмущениям, смещениям объектов и даже к разнообразным интерполяциям изображений. Это Blur-инварианты [27]. В свою очередь известны AMI-инварианты, которые обладают устойчивостью к аффинным преобразованиям [28]. Разработаны комбинированные CBAI-инварианты, объединяющие перечисленные выше достоинства [29].
Пусть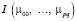 
– инвариант, устойчивый к аффинным преобразованиям, тогда CBAI-инвариантом будет следующий: 
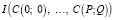, где C(i; j) – Blur-инвариант. Установим порядок вычисления CBAI-инвариантов:
1) поиск начальных моментов:
,
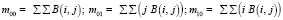где i, j – координаты, а B – функция яркости;
2) нахождение центра масс:
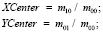
3) нахождение центральных моментов вплоть до седьмого порядка,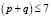 
:
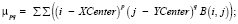
4) поиск Blur-инвариантов вплоть до седьмого порядка:
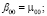
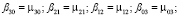
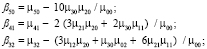
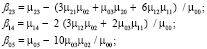
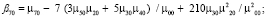
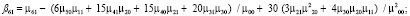
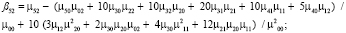
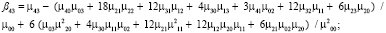
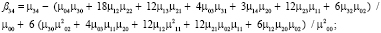
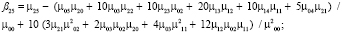
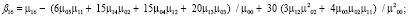
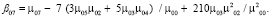
5) поиск CBAI-инвариантов:
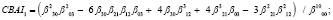
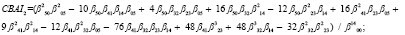
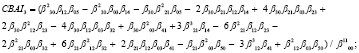
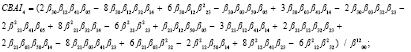
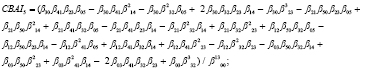
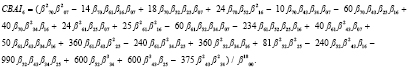
В монографии [15] был найден проективный инвариант в виде бесконечного ряда с произведениями моментов с отрицательными / положительными величинами p и q.
Методы ускорения вычислений с аппаратной поддержкой
Существуют методы построения специализированных алгоритмов и устройств для бортовых систем отображения и обработки графической информации в реальном масштабе времени [30, 31], проблеме построения периодических расписаний с совмещением циклов как наиболее естественных для специализированных устройств, работающих с изображениями, посвящены работы [32, 33]. Решение задач управления и распознавания в бортовых комплексах летательных аппаратов приводит к необходимости вычисления тригонометрических и других элементарных функций, к решению систем линейных и нелинейных уравнений, вычислению сложных арифметических выражений. В условиях ограничений на исполнительные ресурсы задача сводится к оптимизации структур специализированных вычислительных устройств, минимизации аппаратурных затрат и синтезу устройств управления. В этой связи предлагаются методы автоматизации построения вычислителей, оптимизированных под задачи обработки графической информации [34] и управления подсистемами летательных аппаратов [35, 36].
Добавим сюда задачи и функции, реализуемые в системах управления летательными аппаратами [36], включая системы обработки графической информации [37], определения местоположения и ориентации, высокоточного наведения бортовых поворотных камер и др. Решение этих задач реализуется набором функций семейства CORDIC, в состав которого входят операции «множительно-делительная», «поворот», «вектор», «вычисление квадратного корня», прямые и обратные тригонометрические функции [38]. Достоинствами метода CORDIC являются возможность вычисления крупных геометрических и составных операций, преимущество в скорости вычисления элементарных функций по сравнению с методами полиномиальной аппроксимации для последовательных машин; наличие в вычислениях только «коротких» операций сдвига и алгебраического сложения; возможность эффективной реализации, как в специализированных, так и универсальных процессорах. В настоящее время известны такие области применения метода CORDIC, как решение траекторных задач, управление бортовыми камерами, цифровая обработка сигналов, вычисление элементарных функций.
Результаты исследования и их обсуждение
Приведенный в работе обзор показал, что для решения задач распознавания образов целесообразно использовать методы инвариантных моментов. Показано, что в реальных условиях нестабильной внешней среды они являются в общем случае субинвариантами к яркостным шумам или геометрическим преобразованиям аффинного типа. Предложено использование алгоритмов CORDIC в бортовых вычислительных системах. Являясь итерационными, алгоритмы CORDIC имеют естественный параллелизм только на уровне отдельных итерационных формул. Распараллеливание возможно за счет представления ряда функций семейства в виде разрядно-параллельных вычислительных схем [39, 40].
Заключение
Рассмотрены подходы и методы, которые образуют методологическую основу для решения задач распознавания образов в условиях нестабильной внешней среды. Методология включает применение инвариантных моментов, линий положения, нейросетевых классификаторов. Специальный вычислительный метод CORDIC эффективен в бортовых вычислительных комплексах роботизированных систем с ограниченными ресурсами. Прикладная значимость рассмотренных методов и алгоритмов заключается в возможности построения на их основе универсальных инструментальных средств и программного обеспечения, адаптируемого к различным графическим объектам распознавания, включая аэрокосмические снимки.
Исследование выполнено при финансовой поддержке РФФИ: проект № 20-07-00022-а «Разработка и исследование методов распознавания образов на основе инвариантов к яркостным и геометрическим преобразованиям в системах технического зрения беспилотных летательных аппаратов»; проект № 18-07-00025-а «Методы информационно-вычислительной и интеллектуальной поддержки автономного режима функционирования беспилотных летательных аппаратов и их группировок средствами наземных и бортовых станций управления».
Библиографическая ссылка
Абрамов Н.С., Фраленко В.П., Хачумов М.В. ОБЗОР МЕТОДОВ РАСПОЗНАВАНИЯ ОБРАЗОВ НА ОСНОВЕ ИНВАРИАНТОВ К ЯРКОСТНЫМ И ГЕОМЕТРИЧЕСКИМ ПРЕОБРАЗОВАНИЯМ // Современные наукоемкие технологии. – 2020. – № 6-1. – С. 110-117;URL: https://top-technologies.ru/ru/article/view?id=38078 (дата обращения: 21.11.2024).