Вычисление нулей полиномов (наряду с этим употребляется синоним – корни полиномов) исторически связано с основной задачей высшей алгебры, к ее решению сводятся важные приложения в различных областях науки и техники, с ней связаны основные положения квантовой механики [1]. Однако практический поиск нулей полиномов наталкивается на вычислительную неустойчивость, под которой понимается резкий рост погрешности их значений в зависимости от погрешности представления коэффициентов [2; 3]. Другой проблемой оказывается локализация области нулей в случае, если границы их расположения априори неизвестны. Трудности усугубляются, если нули полинома близко расположены (плохо отделены). В частности, это относится к решению проблемы собственных значений матрицы, тогда как высокоточное нахождение всех корней характеристического полинома позволило бы выполнить анализ устойчивости линейной системы обыкновенных дифференциальных уравнений с постоянными коэффициентами [4]. Аналогичные трудности возникают при решении задач безусловной численной оптимизации. Нули и экстремумы функций можно найти классическими методами, но только в условиях вычислительной устойчивости, и если область экстремума априори отделена [5; 6]. Компьютерная идентификация рассматриваемых величин обостряет вычислительные проблемы вследствие обработки данных с плавающей точкой, в случае жестких ограничений длины разрядной сетки. Отчасти альтернативны методы идентификации нулей и экстремумов на основе алгоритмов сортировки [7–9] – в этих способах большинство вычислительных операций заменяются на операции сравнения. На такой основе ниже решается задача построения инвариантного относительно вида входной функции от одной переменной (в продолжение работы – двух переменных) алгоритма компьютерной идентификации экстремумов в случае, когда не указаны границы их совокупного расположения, а также не указан радиус локализации каждого в отдельности экстремума. Нули полиномов и аналитических функций идентифицируются непосредственно как минимумы их абсолютной величины. Аналогично идентифицируются нули функций более общего вида, единственное изменение состоит в том, что значение искомого минимума модуля должно проверяться на достаточное приближение к нулю.
В работе ставится цель построить алгоритм компьютерной идентификации нулей и экстремумов функций одной (в развитии исследования – двух) действительной переменной на основе устойчивой адресной сортировки в качестве основной составляющей алгоритма. Конструируемый алгоритм предполагает инвариантность относительно вида функции. Нули аналитических функций (в частности, полиномов) определяются как минимумы модуля функции. Алгоритм строится без априорного указания границ области экстремумов (нулей), а также без указания радиуса локализации каждого экстремума (нуля) в отдельности. Цель включает изложение способа построения, математико-алгоритмическое обоснование алгоритма, его программную реализацию. Требуется выполнить развернутый численный эксперимент с оценками погрешности вычислений и в дальнейшем показать применение алгоритма к анализу устойчивости линейной системы обыкновенных дифференциальных уравнений. Опираясь на специфику сортировки, предполагается обосновать и наглядно показать вычислительную устойчивость алгоритма и низкую погрешность определения с его помощью искомых величин во всех рассматриваемых применениях. Необходимо, кроме того, выполнить преобразование алгоритма к максимально параллельной форме и дать оценку временной сложности.
Идентификация экстремальных элементов числовой последовательности с произвольно фиксированным радиусом локализации. Пусть дана числовая последовательность
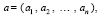(1)
в которой требуется идентифицировать все локально минимальные (локально максимальные) элементы с радиусом локализации r = ε0, где ε0 – произвольно фиксировано. Под локально минимальным (нестрого – «локальный минимум») в границах данного радиуса понимается наименьший элемент среди отсчитанных на ε0 влево и вправо: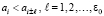 
. Аналогично, локально максимальный элемент («локальный максимум») в этой же окрестности определяется соотношением 
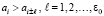. Для идентификации экстремальных элементов ниже используется адресная сортировка по неубыванию со свойством устойчивости (сортировка сохраняет порядок равных элементов). В этом случае экстремальным будет считаться элемент, в определении которого неравенство заменяется на отношение порядка, по которому выполняется сортировка. Первоначально в этом качестве выбирается модифицированная сортировка подсчетом. Для входного массива (1) ее удобно описать матрицей сравнений вида:
(2)
Элемент матрицы (2) определяется функцией знака:
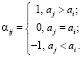
Отсортированный массив обозначается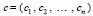 
. Элемент aj входного массива (1) вставляется в выходной массив c по адресу 
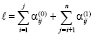, где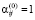 
, если 
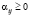, иначе 
; 
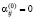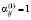, если 
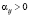, иначе 
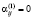. Для подсчитанного индекса 
.
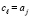Пример 1. Пусть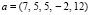 
. Матрица сравнений примет вид (справа для наглядности оставлены только знаки):
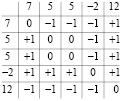
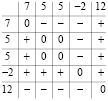
Соотношение для вставки означает следующее: номер j-го элемента входного массива a в отсортированном массиве c подсчитывается как число нулей и плюсов в j-м столбце матрицы над диагональю, включая диагональный элемент, сложенное с числом плюсов под диагональю (нумерация от j = 1). Так,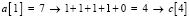 
, 
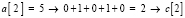. Аналогично, 
, 
, 
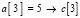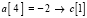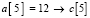. Сортировка сохраняет порядок равных элементов (за счет добавления нуля над диагональю на пересечении столбца текущего элемента и строки предшествующего ему равного элемента). Все адреса вставки имеют единственное значение. В силу взаимной однозначности соответствия входных и выходных индексов получается взаимно однозначная обратная адресация, которая реализуется программно (здесь и ниже – Delphi):
for j:=1 to n do
begin
k:= 0; for i:=1 to j do if a[j]>=a[i] then k:=k+1; for i:=j+1 to n do if a[j]>a[i] then k:=k+1;
c[k]:=a[j]; e[k]:=j;
end;
Если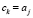 
, то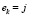 
представляет обратный адрес j-го входного элемента на выходе сортировки. Входной индекс отсортированного элемента запоминается на выходе сортировки как элемент массива e, располагаемый в порядке отсортированных элементов: c[k]:=a[j]; e[k]:=j. Элемент e[k-m] соответствует входному индексу элемента с[k-m], меньшего, чем c[k], для всех m = 1, 2 ,…, k-1. Элемент e[k+m] соответствует входному индексу элемента с[k+m], большего, чем c[k], для всех m = 1, 2 ,…, n-k. Именно это свойство лежит в основе идентификации экстремальных элементов последовательности. Локально минимальный элемент массива a с входным индексом ek, 
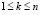, определяется условием
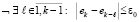, (3)
где r = ε0 – радиус локализации. Фрагмент программной реализации (3) имеет вид
{выполнение процедуры сортировки}
k:=1; while k <= n do
begin for L:=1 to k-1 do if abs(e[k]-e[k-L]) <= eps0 then goto 11; ik:= e[k];
11: k:= k+1 end;
Здесь ik – индекс локально минимального элемента в радиусе eps0 = ε0. Входной индекс любого элемента меньшего ck (с[k]=a[e[k]]) располагается от ek дальше, чем на ε00, поэтому ek – индекс локально минимального элемента в радиусе ε0. Аналогично, локально максимальный элемент определяется из условия, что неравенство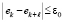 
не должно выполняться ни при одном l, 
, –
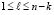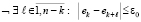. (4)
Программная реализация (4) имеет вид
{выполнение процедуры сортировки}
k:=1; while k <= n do
begin for L:=1 to n-k do if abs(e[k]-e[k+L]) <= eps0 then goto 111; ik:= e[k];
111: k:= k+1 end;
Соотношения (3), (4) и данные программные фрагменты представляют собой условия идентификации локального минимума и, соответственно, максимума (кратко – условия локализации). При этом минимальность и максимальность (наименьший и наибольший элементы в радиусе локализации) здесь и ниже понимаются в смысле отношения порядка в отсортированном массиве. Идентифицированный минимум может оказаться первым (наименьшим), максимум – последним (наибольшим) в цепочке равных элементов. То же имеется в виду всюду, где используется термин «экстремальный элемент». В результате выполнения цикла по k данные условия идентифицируют одновременно все локально минимальные (локально максимальные) в произвольно фиксированном радиусе ε0 элементы последовательности (1). Сортировка используется однократно, затем условия локализации можно применять с любыми значениями радиусов ε0. Идентификация исключает накопление погрешности, поскольку не выполняет вычислений: используются только сравнения элементов при выполнении сортировки и сравнение их индексов для локальной минимизации (максимизации).
Пример 2. Следующая программа идентифицирует все локальные минимумы и максимумы массива из раздела описания констант:
program LokMinMaxI;
{$APPTYPE CONSOLE}
uses
SysUtils;
label 2, 22, 222; const nn=11;
type vect=array [1..nn] of extended; vect0=array [1..nn] of integer;
const b: vect =
(1.20888884+0.00000000000001, 1.20888884-0.00000000000001, 1.20888884, -6.304, 1.404,
-1.904, 9.504, 1.504, 14.604, 1.704, -11.804);
var i,k,l,n: integer; a,c: vect; e: vect0;
procedure sort (var n: integer; var a,c: vect; var e: vect0);
var i,j,k: integer;
begin
for i:=1 to n do
begin k:= 0; for j:=1 to i do if a[j]<=a[i] then k:=k+1; for j:=i+1 to n do if a[j]<a[i] then k:=k+1;
c[k]:=a[i]; e[k]:=i; end;
end;
begin
n:=nn; for i:=1 to n do
a[i]:=b[i]; writeln; writeln; writeln (' ':6, 'massiv a');
for i:=1 to n do write (' ':6, a[i]); writeln; writeln; writeln;
sort (n,a,c,e); writeln (' ':6, 'min eps0=1'); writeln;
k:=1; while k<= n do
begin
for L := 1 to k-1 do if abs(e[k]-e[k- L]) <= 1 then goto 2; writeln (' ',c[k],' ',e[k]);
2: k:=k+1;
end; writeln; writeln; writeln (' ':6, 'max eps0=1'); writeln;
k:=1; while k<= n do
begin
for L := 1 to n-k do if abs(e[k]-e[k+ L]) <= 1 then goto 22; writeln (' ',c[k],' ',e[k]);
22: k:=k+1;
end; writeln; writeln; writeln (' ':6, 'min eps0=3'); writeln;
k:=1; while k<= n do
begin
for L := 1 to k-1 do if abs(e[k]-e[k- L]) <= 3 then goto 222; writeln (' ',c[k],' ',e[k]);
222: k:=k+1;
end; writeln; writeln; writeln (' ':6,'podstanovka indeksov'); writeln;
for i:=1 to n do write (' ':2, ' ', i); writeln; writeln ;
for i:=1 to n do write (' ':2, ' ', e[i]);
readln;
end.
Результат работы программы:
massiv a
1.20888884000001E+0000 1.20888883999999E+0000 1.20888884000000E+0000
-6.30400000000000E+0000 1.40400000000000E+0000 -1.90400000000000E+0000
9.50400000000000E+0000 1.50400000000000E+0000 1.46040000000000E+0001
1.70400000000000E+0000 -1.18040000000000E+0001
min eps0=1
-1.18040000000000E+0001 11
-6.30400000000000E+0000 4
-1.90400000000000E+0000 6
1.20888883999999E+0000 2
1.50400000000000E+0000 8
max eps0=1
1.20888884000000E+0000 3
1.20888884000001E+0000 1
1.40400000000000E+0000 5
9.50400000000000E+0000 7
1.46040000000000E+0001 9
min eps0=3
-1.18040000000000E+0001 11
-6.30400000000000E+0000 4
podstanovka indeksov
1 2 3 4 5 6 7 8 9 10 11
11 4 6 2 3 1 5 8 10 7 9
Пример иллюстрирует точность идентификации локально экстремальных элементов. В массив a включены три элемента a1, a2, a3, взаимно различающиеся на 0.00000000000001. Минимальный из них второй, что отмечено курсивом на выходе программы. Максимальный – третий, что отмечено аналогично. Программа идентифицирует в качестве максимума и первый элемент согласно формальному смыслу условия локализации. Можно продолжить вывод локальных экстремумов с различными радиусами ε0. Все они идентифицируются с точностью до формата представления данных. Чтобы получить глобальный минимум (максимум), в условии локализации достаточно изменить знак неравенства на противоположный при ε0 = 1: if abs(e[k]-e[k- L]) >= 1 then goto … (if abs(e[k]-e[k+ L]) >= 1 then goto …). В конце программы выводится подстановка, образуемая входными индексами k и выходными индексами e[k], располагаемыми в порядке отсортированных элементов c[k]. В общем случае подстановка имеет вид
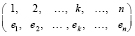. (5)
Она формируется в результате сортировки, в силу устойчивости которой подстановка обладает единственностью. Для идентификации экстремумов условия локализации используют обращение только к элементам перестановки ek. Проверка условий сводится к сравнению этих элементов без преобразований и без изменения их расположения. Отсюда имеет место
Предложение 1. Перестановка индексов в (5), сформированная на основе устойчивой адресной сортировки, содержит всю полноту информации о локально и глобально экстремальных элементах входной последовательности (1) одновременно для всех фиксированных значений радиусов ε0. Эта информация конструктивно извлекается из (5) с помощью условий локализации (3), (4).
Предложение сохраняется для любой сортировки, если она устойчива и в явной форме реализует взаимно однозначное соответствие входных и выходных индексов. При этом экстремальность должна пониматься исключительно в смысле отношения порядка, радиус локализации произвольно фиксирован при циклической проверке условия локализации. Любой экстремальный элемент с произвольным радиусом локализации всегда будет идентифицирован в цикле с фиксированным значением этого радиуса. Экстремумы в смысле строгого неравенства определяются данным способом в качестве частного случая.
Представленный алгоритм обладает максимальным параллелизмом: все операции сравнения сортировки, а также условий локализации взаимно независимы и могут выполняться над готовыми значениями данных. Поэтому в максимально параллельной форме алгоритм может быть реализован с временной сложностью O(1) при любой длине n входной последовательности, число процессоров для поиска одного экстремума O(n2).
Чтобы применить способ к вычислению нулей и экстремумов функции, потребуется сформировать входную последовательность посредством дискретизации функции, выбрать границы числовых параметров и осуществить спуск для идентификации искомых значений с заданной границей погрешности.
Идентификация действительных корней полиномов. С целью численного эксперимента и верификации алгоритма первоначально полином задается разложением по корням:
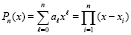. (6)
В данной части работы все корни предполагаются действительными. В программе ниже корни заданы в разделе констант как элементы массива b, с учетом (6) xi = bi, i = 1, 2,...,n. Абсолютная величина полинома задается подпрограммой-функцией func ();. На выходе программы локальные минимумы этой функции должны совпасть с заданными на входе корнями. В разделе констант задается радиус локализации eps0, в качестве его значения можно взять любое число, заведомо меньшее половины наименьшего расстояния между искомыми корнями (в общем случае – между минимумами). Иначе в окрестность такого радиуса могут попасть хотя бы два минимальных элемента, условие локализации исключит один из них, как следствие, не идентифицируется по крайней мере один из корней. Если требуемое расстояние неизвестно, радиус следует взять априори с достаточным запасом малости. В программе ниже корни минимально отделены на 0.001, поэтому eps0=0.00049. Шаг дискретизации задается в разделе констант и определяется значением радиуса локализации: h=eps0/40. В разделе инструкций функция func () дискретизируется, образуя входной массив для сортировки: x:=x0+i*h; a[i]:=func(x);. Согласно эксперименту шаг можно задавать любым значением не большим eps0/33. Однако в случае сложно вычисляемой функции (примеры приведены в дальнейшем) шаг необходимо уменьшить. Значение eps0/40 выбрано для примера, дальнейшее уменьшение шага точности не повысит, но увеличит время выполнения программы. Далее необходимо задать количество сортируемых элементов. Это число может быть зафиксировано произвольно, но с учетом приложения к корням полинома его следует выбрать не меньше 512. Увеличение этого количества не скажется на точности вычислений, но увеличит время работы программы. Для примера в программе взято nn0=1512, имя переменной nn0 заменяет n из (1) (это не имеет отношения к n из (6)). Выбранная длина массива определяет длину отрезка, на котором непосредственно воспроизводится описанная идентификация экстремальных элементов: в программе эта длина обозначается hh и задается оператором hh:=nn0*h. Полный отрезок (область) поиска корней может быть произвольным, но большая его длина замедлит работу программы. Поэтому отрезок выбирается из априорных соображений относительно области корней. В дальнейшем от этого недостатка удается избавиться, для предварительного описания в качестве границ рассматриваемого отрезка выбраны x00=-5; x11=25; отрезок заведомо содержит все искомые корни. Программа начинает работу с левой границы: x0:=x00. Идентификация корней выполняется на текущем отрезке длины hh, который затем циклически сдвигается на свою длину, до достижения правой границы x11. При этом возникает проблема проверки, не лежат ли искомые корни на границах текущего отрезка. Решение заключается в следующем. Значение модуля полинома на границе отрезка длины hh сравнивается с двумя его последовательными значениями слева и с двумя аналогичными значениями справа для проверки минимальности значения на границе. Это выполняют операторы в конце программы for i:= 1 to 2 do begin z:=x+i*h; if func(x) >= func(z) then goto 22; end; и т.д. Собственно на текущем отрезке после выполнения условия локализации идентифицируется (если он есть) локально минимальный элемент xk:= x0+e[k]*h. С точностью до дискретизации и радиуса локализации его значение является приближенным значением корня. Окончательное уточнение выполняется путем циклического спуска к наименьшему значению в сужаемой окрестности приближения. Это делается с помощью процедуры min1 на равномерной сетке из mm=4 элементов. Значение параметра mm можно взять любым большим данного, но практически это замедлит процесс без повышения точности. Сужение окрестности наименьшего значения с переменным диаметром eps1 происходит циклическим делением диаметра eps1:=eps1/1.2 до достижения заданной в заголовке цикла границы погрешности eps1<=eps. Согласно эксперименту делить диаметр можно на любое меньшее 1.2 число при условии, что оно больше единицы. Для искомой точности достаточно данного значения, иначе замедлится работа программы. Процедура min1, как и рассмотренные до сих пор фрагменты алгоритма, не выполняет вычислений, она только сравнивает числовые значения и путем сравнений выбирает наименьшее из них.
Значение корня практически отделяется от других корней полинома согласно построению метода, выполняется локализация отделенного приближения, затем спуск до требуемого уточнения. Вместе с тем необходимо принять во внимание, что изложенный метод теоретически опирается на следствие принципа максимума (минимума) модуля [10]: модуль аналитической функции, отличной от константы и не обращающейся в ноль внутри области аналитичности, не может иметь локальных минимумов внутри этой области. Поэтому локальные минимумы модуля данной функции могут достигаться только в тех точках, где она обращается в ноль (в частности, в ноль обращается ее действительная и мнимая часть). Следствие применимо к полиному (6), где n ≥ 1. В результате к локализованному значению минимума модуля (корня) полинома можно выполнять спуск без опасения, что в окрестность спуска попадет посторонний минимум и станет препятствием для идентификации искомого корня.
Пример 3. Следующая программа идентифицирует все корни полинома 26-й степени вида (6), заданного массивом корней b в разделе констант:
program KORDEMINPOL;
{$APPTYPE CONSOLE}
uses
SysUtils;
label 21, 22; const n1=26;
b: array [1..n1] of extended =
(1, 2, 3, 4.007, 4.008, 5, 6.001, 6.002, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19.003, 19.002, 20, 21, 22, 23);
eps=1E-44; eps0=0.00049; h=eps0/40; n00=1512; mm=4; x00=-5; x11=25;
{x00=0; x11=23;}{x00=-256; x11=256;}
type vect=array [0..4*n00] of extended;vect1=array [0..4*n00] of longint;
vec=array [0..n1] of extended;
var i,j,k,l,ee,nn0: longint; a,c: vect; e: vect1; aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin
p:=1; for i1:=1 to n1 do p:=p*(x-b[i1]); func:=abs(p);
{func:=ln(1+abs(p));}
{func:=abs(exp(exp(-2*abs(x11-x00))*p)-1);}
{func:=abs(sin(x));}
{if x<>0 then func:=abs(sqr(1/x)*1/x*sin(x));}
{if x<>0 then func:=1/x*(exp(abs(sqr(1/x)*1/x*sin(x)))-1);}
{if x<>0 then func:=abs(exp(1/x*sin(x))-1);}
{if x<>0 then func:=ln(1+abs(sin(x)/x*(exp(abs(1/x*sin(x)))-1)));}
{func:=abs(exp(-200*sqr(x-0.3))-1);}
{func:=ln(1+sqrt(exp(-20*(cos(x-0.3)))));}
end;
procedure min1 (var x: extended; var ee: longint);
begin min:=func(x); ee:=0; for i:=1 to mm do
begin x:=xk0+i*h0; if min > func(x) then begin min:=func(x); ee:=i; end; end;
end;
procedure sort(var nn0: longint; var a,c: vect; var e: vect1);
begin
for j:= 1 to nn0 do
begin
k:=0; for i:= 1 to j do if a[j]>=a[i] then k:= k+1; for i:=j+1 to nn0 do if a[j]>a[i] then k:= k+1;
c[k]:=a[j]; e[k]:=j; end;
end;
begin
aaa:=1e62; nn0:=n00; hh:=nn0*h; x0:=x00; while x0 <= x11 do
begin for i:=1 to nn0 do begin x:=x0+i*h; a[i]:=func(x); end;
sort(nn0, a,c, e); k:=1; while k<= nn0 do
begin
for l := 1 to k-1 do if abs(e[k]-e[k-l]) <= eps0/h then goto 22; xk:= x0+e[k]*h;
eps1:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; h0:=abs(2*eps1)/mm;
while abs(eps1) > eps do begin
x:=xk0; min1(x,ee); eps1:=eps1/1.2; xk0:=xk0+ee*h0-eps1; xk1:=xk0+ee*h0+eps1;
h0:=abs(2*eps1)/mm; end;
if func(xk)= 0 then begin x:=xk; goto 21; end; x:=xk0+ee*h0+eps1;
for i:= 1 to 2 do begin z:=x+i*h; if func(x) >= func(z) then goto 22; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x) >= func(z1) then goto 22; end;
if abs(aaa-x) <=1e-20 then goto 22;
21: writeln (' ', x,' ',func(x)); aaa:=x;
22: k:=k+1
end; x0:=x0 + hh end;
readln;
end.
Результат работы программы:
1.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
4.00800000000000E+0000 0.00000000000000E+0000
4.00700000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00100000000000E+0000 0.00000000000000E+0000
6.00200000000000E+0000 0.00000000000000E+0000
7.00000000000000E+0000 0.00000000000000E+0000
8.00000000000000E+0000 0.00000000000000E+0000
9.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0001 0.00000000000000E+0000
1.10000000000000E+0001 0.00000000000000E+0000
1.20000000000000E+0001 0.00000000000000E+0000
1.30000000000000E+0001 0.00000000000000E+0000
1.40000000000000E+0001 0.00000000000000E+0000
1.50000000000000E+0001 0.00000000000000E+0000
1.60000000000000E+0001 0.00000000000000E+0000
1.70000000000000E+0001 0.00000000000000E+0000
1.80000000000000E+0001 0.00000000000000E+0000
1.90020000000000E+0001 0.00000000000000E+0000
1.90030000000000E+0001 0.00000000000000E+0000
2.00000000000000E+0001 0.00000000000000E+0000
2.10000000000000E+0001 0.00000000000000E+0000
2.20000000000000E+0001 0.00000000000000E+0000
2.30000000000000E+0001 0.00000000000000E+0000
В левой колонке – значение корня, в правой – значение полинома в корне. Таким образом, корни полинома 26-й степени, среди которых три пары взаимно отделены на 0.001 (отмечены курсивом), идентифицированы с точностью до формата представления данных. Не оговоренные программные операторы имеют смысл, связанный с наглядностью вывода, они дополнительно обсуждаются в дальнейшем. Закомментированные функции и области поиска используются ниже. Программа сохраняет правильность идентификации на любом промежутке при любой малой отделенности корней (при «произвольной» степени полинома), но в данной версии переход к таким параметрам влечет риск неприемлемого замедления работы. При переходе к быстрой сортировке (в дальнейшем будет использоваться сортировка слиянием) точность идентификации за приемлемое время можно сохранить в случае взаимной отделенности корней на величину, существенно меньшую 0.001. Это достигается на отрезке сравнительно большой длины, включающем все корни полинома высокой степени [8].
В дальнейшем наряду с положительными примерами обсуждаются трудности, возникающие вследствие ограниченности числового диапазона, объема оперативной памяти, а также недостаточной точности стандартных программ, с помощью которых определяются элементы входного массива.
Идентификация нулей трансцендентных функций одной действительной переменной. Искомые нули, в случае если функции аналитические, идентифицируются без изменения алгоритма и программы, представленных для идентификации действительных корней полиномов. Достаточно вместо модуля полинома подать на вход программы модуль функции. Чтобы, по возможности, ничего не менять в программе KORDEMINPOL примера 3, вначале рассматривается более сложная задача: функции будут взяты как суперпозиции от полиномов, в частности от полинома, представленного в этой программе. Так, если вместо корней полинома (6) искать нули функции
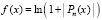, (7)
то в подпрограмме func (…), задающей функцию, после предварительного задания полинома, в завершающем операторе присваивания вместо func:=abs(p); следует поставить оператор func:=abs(ln(1+abs(p)));. Больше ничего менять не нужно, результатом работы программы будет тот же набор корней в той же последовательности и с той же точностью. Очевидно, это правильный результат поиска нулей функции (7). Для программной реализации данного примера достаточно удалить знаки фигурных скобок первого комментария в подпрограмме func (…) программы KORDEMINPOL. В качестве другого примера рассматривается поиск нулей функции
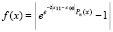, (8)
где в показателе используется длина отрезка поиска корней полинома (в программе примера 3 x00=-5; x11=25;). Аналогично предыдущему, в завершающем операторе подпрограммы func (…) программы KORDEMINPOL примера 3 следует поставить оператор func:=abs(exp(exp(-2*abs(x11-x00))*p)-1); (удалить знаки фигурных скобок второго комментария в подпрограмме func (…)). В результате нули функции (8) совпадут с корнями полинома из этой же программы, однако границы отрезка поиска нулей придется сузить: x00=1; x11=23;.
Замечание 1. Если отрезок поиска не сужать, оставив прежним, произойдет выход за границы числового диапазона. В показателе степени (8) программа задает полином 26-й степени, на границе исходного отрезка он берется от числа 25. В таком виде он попадет в показатель степени экспоненты, что влечет выход из числового диапазона. Именно поэтому в (8) перед Pn(x) в показателе степени введена весовая экспонента с отрицательным показателем. Если рассматривать аналог (8) без такого веса, а просто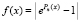 
, то допустимый отрезок поиска нулей резко сузится. В этом случае нули правильно найдутся на отрезке [–1, 5]. Соответственно, их количество станет 6, это требует изменить степень полинома в программе до n1=6. В таком варианте нули вне данного отрезка не будут найдены по построению. Последовательными фрагментами по отрезкам длины 6 и полиномами 6-й степени с расположенными на них корнями проходится весь исходный отрезок с правильной идентификацией расположенных на текущих отрезках корней, но это не является корректным решением задачи для полинома 26-й степени.
В дополнение к замечанию можно отметить, что программа все же устойчиво справляется с задачей поиска нулей функции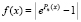 
при n = 10 на отрезке длины 9.
В случае если предложенный способ не сталкивается с выходом из границ числового диапазона, программа работает правильно и устойчиво.
Пример 4. Пусть требуется найти нули функции
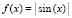(9)
на отрезке –256 ≤ x ≤ 256. Если в программе примера 3 задать x00=-256; x11=256; кроме того, в подпрограмме func (…) выполнить func:=abs(sin(x)); (без формирования значения полинома, степени и корней, что в данном случае излишне), то программа идентифицирует правильный набор нулей функции (9). Для наглядности можно выводить не только аргумент x, обращающий (9) в ноль, но и соответственное значение x/π. Получится следующий результат работы программы:
-2.54469004940773E+0002 -8.10000000000000E+0001 3.30681662608079E-0018
-2.51327412287183E+0002 -8.00000000000000E+0001 8.67361737988404E-0019
-2.48185819633594E+0002 -7.90000000000000E+0001 1.57209315010398E-0018
-2.45044226980004E+0002 -7.80000000000000E+0001 4.01154803819637E-0018
…………………………………………………………………………………………
-6.28318530717959E+0000 -2.00000000000000E+0000 1.08420217248550E-0019
-3.14159265358979E+0000 -1.00000000000000E+0000 5.42101086242752E-0020
1.71189937630016E-0044 5.44914495628207E-0045 1.71189937630016E-0044
3.14159265358979E+0000 1.00000000000000E+0000 5.42101086242752E-0020
6.28318530717959E+0000 2.00000000000000E+0000 1.08420217248550E-0019
………………………………………………………………………………………...
2.45044226980004E+0002 7.80000000000000E+0001 4.01154803819637E-0018
2.48185819633594E+0002 7.90000000000000E+0001 1.57209315010398E-0018
2.51327412287183E+0002 8.00000000000000E+0001 8.67361737988404E-0019
2.54469004940773E+0002 8.10000000000000E+0001 3.30681662608079E-0018
Целочисленные значения x/π во второй колонке показывают, что не пропущен ни один корень функции (9). Радиус локализации можно уменьшить до значения близкого к π/2 (при условии eps0 < pi/2). Например, можно выбрать eps0=0.49;. Результат не изменится, хотя будет нарушаться порядок выводимых значений.
К аналогичному результату, без изменения параметров примера 4, приведет поиск нулей функции
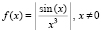, (10)
если в подпрограмме func (…) выполнить if x<>0 then func:=abs(sqr(1/x)*1/x*sin(x));. Значение функции в третьей колонке уменьшится до 10-25 за счет роста знаменателя в (10).
Если рассмотреть экспоненту с ограниченным показателем, то выхода из границ диапазона не произойдет. Пусть, например,
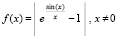. (11)
Для поиска нулей функции (11) (–256 ≤ x ≤ 256) в предыдущем варианте программы требуется единственное изменение: if x<>0 then func:=abs(exp(1/x*sin(x))-1);. Результат повторится с той разницей, что в третьей колонке будут только нулевые значения.
Инвариантность метода иллюстрирует пример
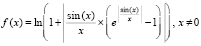, –256 ≤ x ≤ 256. (12)
В последнем видоизменении программы задается функция (12): if x<>0 then func:=ln(1+abs(sin(x)/x*(exp(abs(1/x*sin(x)))-1)));. Результат работы программы не изменится, с той, однако, разницей, что во второй колонке значения аргумента окажутся верными лишь 8 значащих цифр десятичной мантиссы. Эта неточность предположительно связана с недостатком точности библиотеки стандартных программ, третья колонка состоит из нулевых значений. В таких случаях погрешность иногда можно снизить с помощью следующего приема. В рассматриваемой программе KORDEMINPOL определяются две подпрограммы-функции: func11() – эта подпрограмма задает функцию, у которой требуется найти корни (рассматриваемом случае – функцию (12)), и func () – эта подпрограмма задает такую функцию, у которой аналитически те же корни, но программно они идентифицируются точнее. В суперпозиции (12) в качестве func () можно взять внутреннюю функцию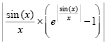 
:
function func11 (var x: extended): extended;
var i1: 1..n1;p:extended;
begin
if x<>0 then func11:=abs(ln(1+abs(sin(x)/x*(exp(abs(1/x*sin(x)))-1))));
end;
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin
if x<>0 then func:=abs(sin(x)/x*(exp(abs(1/x*sin(x)))-1));
end;
Далее все действия выполняются для внутренней функции func () без изменения программы, за исключением того, что корни подставляются «как для проверки» в исходно заданную функцию (12), которая теперь представлена подпрограммой func11(). Иными словами, выводится не func (), а func11 () от найденных значений корней. В этом случае вывод осуществляется в виде
21: writeln (' ', x,' ',x/pi,' ',func11(x)); aaa:=x;
Результат работы программы с этими изменениями, при значении параметров eps0=0.0049; h=eps0/40; x00=-256; x11=256; примет вид:
-2.54469004940773E+0002 -8.10000000000000E+0001 0.00000000000000E+0000
-2.51327412287183E+0002 -8.00000000000000E+0001 0.00000000000000E+0000
-2.48185819633594E+0002 -7.90000000000000E+0001 0.00000000000000E+0000
-2.45044226980004E+0002 -7.80000000000000E+0001 0.00000000000000E+0000
……………………………………………………………………………………………
-3.14159265358979E+0000 -1.00000000000000E+0000 0.00000000000000E+0000
3.14159265358979E+0000 1.00000000000000E+0000 0.00000000000000E+0000
6.28318530717959E+0000 2.00000000000000E+0000 0.00000000000000E+0000
9.42477796076938E+0000 3.00000000000000E+0000 0.00000000000000E+0000
……………………………………………………………………………………………
2.45044226980004E+0002 7.80000000000000E+0001 0.00000000000000E+0000
2.48185819633594E+0002 7.90000000000000E+0001 0.00000000000000E+0000
2.51327412287183E+0002 8.00000000000000E+0001 0.00000000000000E+0000
2.54469004940773E+0002 8.10000000000000E+0001 0.00000000000000E+0000
Погрешности во второй колонке (x/π) не проявились, значения функции (12) в каждом корне равны нулю с точностью до формата представления данных. Изложенный прием не универсален, дан для случая явно заданной суперпозиции, но в дальнейшем будут представлены полезные аналоги для функций комплексных переменных.
Заключительный пример данного раздела – вычисление гауссиана
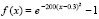. (13)
Единица в правой части вычитается для сохранения общей схемы. С параметрами
eps=1E-44; eps0=0.0049; h=eps0/40; n00=1512; mm=4; x00=-2; x11=2; (14)
и функцией func:=abs(exp(-200*sqr(x-0.3))-1); программа идентифицирует нулевую правую часть (13) в точке 2.99999999988358E-0001.
Замечание 2. Изложенный метод практически не использует область аналитичности функций. В некоторых примерах функция на вход программы поступает с разрывами производных, требуемую локализацию минимумов модуля программа реализует по построению. Эта ее особенность будет использоваться при вычислении экстремумов функций, не взятых по абсолютной величине.
Идентификация экстремумов функций одной действительной переменной. Если радиус локализации минимумов eps0 меньше половины расстояния между точками ближайших друг к другу минимумов, то программа KORDEMINPOL примера 3 почти без изменений выполнит идентификацию всех локальных минимумов с радиусом локальной минимальности eps0: на вход должна поступать непосредственно сама функция без знака модуля. Еще одно изменение состоит в том, что следует убрать ограничение на приближение значения функции к нулю (берется в комментарий {if abs(aaa-x) <=1e-20 then goto 22;}).
Пример 5. Пусть требуется найти все минимумы функции
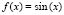
на отрезке –256 ≤ x ≤ 256. В подпрограмме func (…) программы KORDEMINPOL следует выполнить func:= sin(x);. Если для наглядности во второй колонке выводить x/(2π)-3/4, то результат работы программы примет вид:
-2.52898208614211E+0002 -4.10000000000371E+0001 -1.00000000000000E+0000
-2.46615023307032E+0002 -4.00000000000371E+0001 -1.00000000000000E+0000
-2.40331837999852E+0002 -3.90000000000371E+0001 -1.00000000000000E+0000
…………………………………………………………………………………………
1.09955742873314E+0001 9.99999999962944E-0001 -1.00000000000000E+0000
1.72787595945110E+0001 1.99999999996294E+0000 -1.00000000000000E+0000
2.35619449016906E+0001 2.99999999996294E+0000 -1.00000000000000E+0000
………………………………………………………………………………………….
2.43473430652976E+0002 3.79999999999629E+0001 -1.00000000000000E+0000
2.49756615960156E+0002 3.89999999999629E+0001 -1.00000000000000E+0000
2.56039801267335E+0002 3.99999999999629E+0001 -1.00000000000000E+0000
Минимумы найдены правильно, среди точек минимума нет пропущенных. Аналогичный результат получится для функции
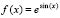, –256 ≤ x ≤ 256.
При этом точки минимума – те же, все значения минимумов равны 3.67879441171442E-0001, то есть, e-1. Для функции
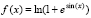, –256 ≤ x ≤ 256
получатся те же точки минимумов, все значения минимумов равны 3.13261687518223E-0001, то есть ln(1 + e-1). Чтобы убедиться в правильности значения, достаточно в каждой точке выводить func(x)-ln(1+exp(-1)), что даст ноль на выходе программы.
Наконец, вместо (13) рассматривается непосредственно гауссиан:
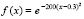. (15)
Его максимум идентифицируется как минимум функции с обратным знаком: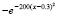 
. В подпрограмме func (…) программы KORDEMINPOL задается func:=-exp(-200*sqr(x-0.3)). С параметрами (14), при условии вывода -func(x), на выходе программы получится:
2.99999999988358E-0001 1.00000000000000E+0000 (16)
Аналогичным способом всегда можно идентифицировать локальные максимумы. Вместе с тем верный результат получится при непосредственном использовании программного фрагмента, реализующего условия (4). Для этого потребуются следующие изменения в рассматриваемой программе. Во-первых, функция в подпрограмме func (…) задается без абсолютной величины и без обратного знака, непосредственно в программной записи математического выражения. В частности, гауссиан (15) задается в виде func:=exp(-200*sqr(x-0.3));. Во-вторых, в процедуре min1 ищется не наименьший, а наибольший элемент, поэтому знак неравенства в этой процедуре следует изменить на противоположный: x:=xk0+i*h0; if min > func(x) then … В-третьих, условие локализации минимума меняется на условие локализации максимума: for L := 1 to nn0-k do if abs(e[k]-e[k+L]) <= eps0/h then goto 22;. Заключительное изменение касается проверки экстремальности на границах текущего отрезка длины hh, где в этом случае проверяется не минимальность, а максимальность, и в соответствующих операторах изменится знак неравенства: z:=x+i*h; if func(x) < func(z) then goto 22; … z1:=x-i*h; if func(x) < func(z1) then goto 22;. При выводе локально максимального значения знак функции не меняется. С такими видоизменениями программа примера 3 будет правильно идентифицировать все локальные максимумы с произвольно фиксированным радиусом локализации в представленных границах погрешности. В частности, для гауссиана (15), при сохранении параметров (14), получатся верные значения (16). Если в качестве примера рассмотреть функцию
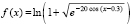
и искать ее локальные максимумы на отрезке –256 ≤ x ≤ 256, то в подпрограмме func (…) следует задать func:=ln(1+sqrt(exp(-20*(cos(x-0.3))))). Чтобы убедиться, что программа не пропускает максимумов, нужно во второй колонке выводить (x-0.3)/(2*pi)-1/2.
Результат работы программы:
-2.54169004941006E+0002 -4.10000000000371E+0001 1.00000453988992E+0001
-2.47885819633826E+0002 -4.00000000000371E+0001 1.00000453988992E+0001
-2.41602634326647E+0002 -3.90000000000371E+0001 1.00000453988992E+0001
-2.35319449019467E+0002 -3.80000000000371E+0001 1.00000453988992E+0001
....………………………………………………………………………………………
2.35919449019002E+0002 3.69999999999629E+0001 1.00000453988992E+0001
2.42202634326181E+0002 3.79999999999629E+0001 1.00000453988992E+0001
2.48485819633361E+0002 3.89999999999629E+0001 1.00000453988992E+0001
2.54769004940540E+0002 3.99999999999629E+0001 1.00000453988992E+0001
Таким образом, идентифицируются все локальные максимумы рассматриваемой функции. В правильности их значения можно убедиться, выводя разность между идентифицированным максимумом и его «истинным» значением: func(x)-ln(1+sqrt(exp(20))). Это даст нули в третьей колонке.
Замена сортировки. Численный эксперимент можно расширить, программу примера 3 преобразовать в практически более значимую, если процедуру сортировки подсчетом заменить процедурой более быстрой сортировки слиянием. Такая процедура с заголовком procedure sort(var nn0: longint; var c: vect1; var e: vect2); в дальнейшем применяется для идентификации комплексных корней полиномов и экстремумов функций двух действительных переменных. Она обладает всеми перечисленными вначале качествами для корректного применения, в последовательном варианте ее временная сложность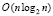 
, что обеспечивает более высокое быстродействие по сравнению с сортировкой подсчетом, которая в последовательном варианте имеет сложность O(n2). Сортировка слиянием реализована с одним массивом c для входных и выходных элементов, представление в разделе описаний сохраняется в дальнейшем. Меняется формирование сортируемого массива: вместо операторов for i:=1 to nn0 do begin x:=x0+i*h; a[i]:=func(x); end; sort(nn0, a,c, e); необходимо взять for i:=1 to nn0 do begin x:=x0+i*h; с[i]:=func(x); end; sort(nn0, c, e);. Ниже программа с данными изменениями приводится для массива корней полинома (6), однако с меньшей, чем в программе примера 3, взаимной отделенностью. В то же время их поиск будет выполняться на отрезке большей длины.
Пример 6. Измененная программа примет вид:
program KORDEMINPOLsortnew;
{$APPTYPE CONSOLE}
uses
SysUtils;
label 21, 22; const n1=26;
b: array [1..n1] of extended =
(1, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19.0003, 19.0002, 20, 21, 22, 23);
eps=1E-44; eps0=0.000049; h=eps0/33; n00=1512; mm=4; x00=-15; x11=70;
type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint;
vec=array [0..n1] of extended;
var i,j,k,l,ee,nn0: longint; a,c: vect1; e: vect2; b1:vec;
aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1: extended;
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p:=1; for i1:=1 to n1 do p:=p*(x-b1[i1]); func:=abs(p); end;
procedure min1 (var x: extended;var ee:longint);
begin min:=func(x); ee:=0; for i:=1 to mm do begin
x:=xk0+i*h0; if min > func(x) then begin min:=func(x); ee:=i; end;end;end;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
type vecc=array[0..4*n00] of longint;
var ab:integer; i,j,k,l,m,r,nm,p,n: longint; e1, e2: vecc;
begin
p := trunc(ln(nn0)/ln(2)); if p<> ln(nn0)/ln(2) then p := p+1;
n := round(exp(p*ln(2)));
for l := 1 to n do if l<=nn0 then e[l] := l else ab:=1;
for r := 1 to p do begin m :=round(exp(r*ln(2))); nm:=n div m;
for k := 0 to nm-1 do begin
for l := 1 to m div 2 do begin
if (k * m + l > nn0) or (e[k * m + l]>nn0) then ab := l
else e1[l] := e[k * m + l];
if (k * m + m div 2+ l > nn0) or (e[k * m + m div 2+ l]>nn0) then ab := 1
else e2[l] := e[k * m + m div 2 + l] end;
i := 1; j := 0; while i + j <= m do begin
if i = m div 2 + 1 then ab := -1;
if j = m div 2 then ab := 1;
if (k * m + i > nn0) or (e[k * m + i]>nn0)
or (k * m + m div 2 + j > nn0-1) or (e[k * m + m div 2+ j]>nn0)
then ab:=1;
if (i <= m div 2) and (j <= m div 2 -1) and (k * m + i<= nn0)
and (k * m + m div 2 + j <= nn0-1)
then if (e2[j + 1] > nn0) or (e1[i]> nn0) then ab := 1 else
begin if c[e2[j + 1]] - c[e1[i]]= 0 then ab := 0;
if c[e2[j + 1]] - c[e1[i]]> 0 then ab := 1;
if c[e2[j + 1]] - c[e1[i]]< 0 then ab := -1
end; if ab >= 0 then
begin e[k * m + i + j] := e1[i]; i := i + 1 end
else begin e[k * m + i + j] := e2[j + 1]; j := j + 1 end
end end end end;
begin
aaa:=1e62; nn0:=n00; hh:=nn0*h;
x0:=x00; for i:=1 to n1 do b1[i]:=b[i]; while x0 <= x11 do
begin for i:=1 to nn0 do begin x:=x0+i*h; c[i]:=func(x); end;
sort(nn0, c, e); k:=1; while k<= nn0 do
begin for l := 1 to k-1 do if abs(e[k]-e[k-l]) <= eps0/h then goto 22; xk:= x0+e[k]*h;
eps1:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; h0:=abs(2*eps1)/mm;
while abs(eps1) > eps do begin x:=xk0; min1(x,ee); eps1:=eps1/1.2;
xk0:=xk0+ee*h0-eps1; xk1:=xk0+ee*h0+eps1; h0:=abs(2*eps1)/mm; end;
if func(xk)= 0 then begin x:=xk; goto 21; end; x:=xk0+ee*h0+eps1;
for i:= 1 to 2 do begin z:=x+i*h; if func(x) >= func(z) then goto 22; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x) >= func(z1) then goto 22; end;
if abs(aaa-x)<=1e-20 then goto 22;
21: writeln (' ', x,' ',func(x)); aaa:=x;
22: k:=k+1 end; x0:=x0 + hh end;
readln;
end.
Результат работы программы аналогичен примеру 3, с тем исключением, что среди идентифицированных есть корни, взаимно отделенные на 0.0001:
4.000800000000000E+0000 0.00000000000000E+0000
4.000700000000000E+0000 0.00000000000000E+0000
…………………………………………………………..
6.000100000000000E+0000 0.00000000000000E+0000
6.000200000000000E+0000 0.00000000000000E+0000
…………………………………………………………..
1.900020000000000E+0001 0.00000000000000E+0000
1.900030000000000E+0001 0.00000000000000E+0000
Поиск корней выполнялся на отрезке с границами x00=-15; x11=70;. Тот же результат, но более медленно достигается, например, на отрезке x00=-70; x11=70;.
От известных методов предложенный отличается [11] по построению, инвариантным условиям применения и минимизацией погрешности.
Необходимо отметить, что исходная сортировка подсчетом обладает максимальным параллелизмом. Общая оценка времени для алгоритма с ее применением приводится непосредственно ниже.
Временная сложность максимально параллельной формы. Временная сложность алгоритма (условно – время) измеряется числом последовательных шагов его выполнения. Для упрощения обозначений использованный выше идентификатор длины массива nn0 при выполнении оценок временной сложности заменяется на n (n=nn0). Это обозначение не связано со степенью полинома (6). Как отмечалось, модифицированная сортировка подсчетом обладает максимально параллельной формой. При любой длине входной последовательности n ее временная сложность оценивается как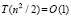 
, в скобках слева – число процессоров. Все сравнения условия локализации также взаимно независимы, значения данных для них готовы. Для одного k они могут выполняться синхронно за время O(1), с учетом (3) 
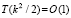. Выполнение этих условий взаимно независимо по 
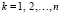. Для всего множества индексов k условия (3) реализуемы синхронно с оценкой 
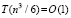. Поиск наименьшего значения в подпрограмме min1 можно заменить сортировкой подсчетом (наибольший элемент в конце отсортированного массива, наименьший – в начале). В параллельной форме преобразованная подпрограмма выполнима с оценкой O(1). Число шагов спуска от локализованного минимума с радиусом ε0 (eps0) к его приближению с заданной границей погрешности ε (в программе eps=1E-44;) определяется сужением радиуса локализации в d > 1 раз на шаге (значение d относительно близко к единице, в программе d = 1.2). Отсюда следует, что 
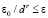, где r – число шагов спуска. Тогда 
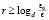, и можно выбрать 
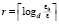. В результате временная сложность отдельно взятого параллельного спуска составит
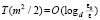. (17)
С учетом того, что спуск формально может потребоваться для всех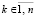 
, оценка (17) перейдет в оценку вида 
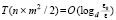. Максимальное число процессоров потребуется при выполнении условий локализации одновременно по всем индексам отсортированных элементов. Поскольку сортировка, локализация и спуск выполняются последовательно друг за другом, то этого (максимального) числа процессоров достаточно для выполнения всех рассмотренных фрагментов идентификации. Таким образом, на текущем отрезке длины hh максимально параллельная форма алгоритма идентификации всех нулей полинома имеет временную сложность 
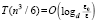. На всех этих отрезках выполнение алгоритма взаимно независимо и может производиться одновременно. Проверка условия экстремальности граничных значений выполнима синхронно по всем границам за единичное время (на отдельном процессоре на каждой границе). Остается учесть число рассматриваемых отрезков. Обозначая отрезок полного поиска [x00, x11], учитывая, что длина hh текущего отрезка определяется значением n×h, где в свою очередь 
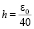, искомое число можно представить в виде: 
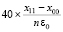. С таким коэффициентом надо взять количество процессоров на отрезке полного поиска. Окончательно оценка временной сложности максимально параллельной формы поиска всех действительных нулей полинома примет вид
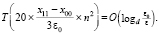(18)
Если параметры в правой части (17), (18) считать постоянными, то она имеет единичный порядок, в этом случае максимально параллельное выполнение изложенного алгоритма имеет порядок временной сложности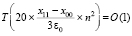 
.
От параллельных схем вычислительной линейной алгебры [12] предложенный метод отличается максимально параллельной формой.
Идентификация области действительных корней полинома с действительными коэффициентами. Аналитические оценки границ области корней рассматриваются в дальнейшем, – они не всегда точны, как правило, не даются, если коэффициенты полинома априори неизвестны. Целесообразно уметь применять предложенный метод, когда область расположения корней неизвестна. В этом случае определение границ и структуры области можно выполнить непосредственно с помощью программы, по которой идентифицируются корни. В частности, можно воспользоваться программой KORDEMINPOLsortnew примера 6. Нужно выбрать сравнительно большой радиус локализации и выполнить программу без каких-либо других изменений на отрезке большой длины, с границами, заведомо включающими все искомые корни. Так, с радиусом локализации eps0=0.049 можно взять границы x00=-1000; x11=1000;. Результатом работы программы для корней из раздела констант окажутся значения
1.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
4.00070000000000E+0000 0.00000000000000E+0000
……………………………………………………………
2.10000000000000E+0001 0.00000000000000E+0000
1.90002000000000E+0001 0.00000000000000E+0000
2.20000000000000E+0001 0.00000000000000E+0000
2.30000000000000E+0001 0.00000000000000E+0000
В качестве границ области корней [x00, x11] можно взять наименьшее и наибольшее из значений левой колонки с отступом eps0. Среди приближений корней есть показывающие структуру их взаимного расположения по значащим цифрам разрядов мантиссы. В любом случае в идентифицированных границах без опасения можно уменьшить радиус локализации до eps0=0.000049;. С исходными параметрами примера 6 в найденных границах программа без погрешности в формате представления данных определит все корни полинома.
Замечание 3. Описанное нахождение области корней опирается на следствие принципа максимума (минимума) модуля: модуль аналитической функции, отличной от константы и не обращающейся в ноль внутри области аналитичности, не может иметь локальных минимумов внутри этой области. Полином аналитичен и не обращается в ноль всюду вне области корней, поэтому локальных минимумов модуля вне области корней он не имеет. Кроме того, модуль полинома монотонно растет при удалении от границ этой области. Поэтому если в рассмотренной программе взять заведомо далекие от области корней границы, а радиус локализации относительно малым, то программа с необходимостью определит минимумы из области корней с точностью до радиуса локализации. Можно организовать итерации, на каждой из которых границы расширяются, а радиус локализации одновременно уменьшается в заданной пропорции, – процесс программной идентификации необходимо сойдется к области корней. С отступом на значение радиуса от наименьшего и наибольшего из корней получатся границы области. При неудачном выборе начальных границ и недостаточно малом радиусе локализации программа может не найти минимумов (они отфильтруются меньшими значениями внутри или вне области). Этого не произойдет, если сам радиус заведомо меньше половины диаметра области корней, а начальные границы будут отстоять от всех корней на расстояние многих радиусов. В этом случае программа локализует минимум модуля полинома и выполнит спуск к локализованному значению тогда и только тогда, когда в окрестность локализации попал корень этого полинома. При этом наименьшее и наибольшее из приближений корней с точностью до радиуса определяют границы области всех корней полинома.
Найденные границы могут оказаться грубыми при выборе большого радиуса локализации (большой радиус нужен, чтобы сократить длительность процесса идентификации): в окрестности данного радиуса возможна фильтрация левосторонних и правосторонних корней. Требуемая алгоритмизация состоит в поэтапном уточнении границ посредством уменьшения радиуса локализации. Если при уменьшении радиуса результат работы программы кратно повторяется, то границы области корней определены окончательно. Так, в рассмотренном примере те же границы будут идентифицированы на [–100, 200] с радиусом eps0=0.0049 и на [–10, 50] с радиусом eps0=0.00049. Естественно перейти к окончательной идентификации с заведомо малым радиусом eps0=0.000049, что повлечет совпадение числа различных корней со степенью полинома. Это завершит процесс поиска.
Замечание 4. В рассмотренных примерах все корни полиномов были различными. Всюду в дальнейшем, пока не оговорено иное, также предполагается, что все корни полинома различны, их количество равно степени полинома. Случай кратных корней будет рассмотрен в продолжении излагаемой работы.
Данным способом границы области корней идентифицируются при любом разбросе корней на действительной оси. Например, можно взять корни в последовательности
b: array [1..n1] of extended = (-100, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19.0003, 19.0002, 210, 210.0001, 22, 23);
При выборе параметров
eps=1E-44; eps0=0.049; h=eps0/33; n00=1512; mm=4; x00=-1000; x11=2000;
программа даст следующий результат:
-1.00000000000000E+0002 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
4.00070000000000E+0000 0.00000000000000E+0000
……………………………………………………………
2.20000000000000E+0001 0.00000000000000E+0000
2.30000000000000E+0001 0.00000000000000E+0000
2.10000100000000E+0002 0.00000000000000E+0000
2.10000000000000E+0002 0.00000000000000E+0000
Далее в границах x00=-110; x11=220; можно непосредственно выполнить правильную идентификацию всех корней, взяв eps0=0.000049. Как отмечалось, способ дает структуру расположения корней. Можно выделить отрезки, которые содержат сгруппированные корни и находятся на сравнительно большом взаимном удалении: x00=-110; x11=-90; x00=-10; x11=50; и x00=190; x11=220;. На каждом из таких отрезков можно повторить работу программы при eps0=0.000049. Это даст правильный результат за меньшее время, чем при идентификации в общих границах.
Инвариантным и полностью автоматизируемым представляется следующее видоизменение только что изложенного способа. Вся полная программа идентификации корней полинома преобразуется в процедуру (в примере ниже: ident(x00,x11,eps0, h)). Границы области поиска и радиус локализации делаются переменными и становятся парметрами процедуры. На отрезке с начальными границами, заведомо включающими область корней (в примере ниже x00:=-320; x11:=320;), с первичным радиусом локализации eps0 (в примере ниже eps0:=0.00049), позволяющим идентифицировать область, выполняются приближения корней. Приближения окажутся взаимно отделенными на величину не менее двух радиусов (одного диаметра). На выходе процедуры приближения корней запоминаются как элементы массива (rex[kk]:=x;). Затем в цикле по числу элементов этого массива, в окрестности диаметра 2eps0 каждого приближения корня, повторяется обращение к той же процедуре с новым радиусом локализации, заведомо меньшим половины расстояния между ближайшими искомыми корнями (в примере взято eps0/10). В результате правильно определятся все корни, включая отделенные на уменьшенный двойной радиус локализации (eps0/10).
Пример 7. Ниже реализовано только что описанное видоизменение программы. С помощью видоизмененной программы находятся все корни полинома 26-й степени, заданные в разделе констант массивом b:
program ITERPROCEDURE;
{$APPTYPE CONSOLE}
uses
SysUtils;
const n1=26;
b: array [1..n1] of extended = (-100, 2, 3, 4.0007, 4.0008, 5, 6.0001, 6.0002, 7, 8, 9, 10, 11, 12, 13,
14, 15, 16, 17, 18, 19.0003, 19.0002, 210, 210.0001, 22, 23);
eps=1E-44; n00=1512; mm=4;
type vect1=array [0..4*n00] of extended; vect2=array [0..4*n00] of longint; vec=array [0..n1] of extended;
var i,j,k,l,ee,nn0,kk,kk1: longint; a,c: vect1; e: vect2; b1:vec; rex:vect1;
aaa,x,x0,x1,xk,xk0,xk1,h0,min,eps1,hh,z,z1,x00,x11,eps0,h,eps00: extended;
procedure sort(var nn0:longint; var c: vect1; var e: vect2);
{процедура сортировки слиянием без изменения скопирована
из программы KORDEMINPOLsortnew примера 6}
procedure ident (var x00,x11,eps0, h: extended);
label 21, 22;
function func (var x: extended): extended;
var i1: 1..n1;p:extended;
begin p:=1; for i1:=1 to n1 do p:=p*(x-b1[i1]); func:=abs(p); end;
procedure min1 (var x: extended;var ee:longint);
begin min:=func(x); ee:=0; for i:=1 to mm do begin
x:=xk0+i*h0; if min > func(x) then begin min:=func(x); ee:=i; end;end;end;
begin
aaa:=1e62;nn0:=n00; hh:=nn0*h;kk:=0;
x0:=x00; for i:=1 to n1 do b1[i]:=b[i];
while x0 <= x11 do
begin
for i:=1 to nn0 do begin x:=x0+i*h; c[i]:=func(x); end;
sort(nn0, c, e); k:=1; while k<= nn0 do
begin
for l := 1 to k-1 do if abs(e[k]-e[k-l]) <= eps0/h then goto 22; xk:= x0+e[k]*h;
eps1:=eps0; xk0:=xk-eps1; xk1:=xk+eps1; h0:=abs(2*eps1)/mm;
while abs(eps1) > eps do
begin x:=xk0; min1(x,ee); eps1:=eps1/1.2; xk0:=xk0+ee*h0-eps1; xk1:=xk0+ee*h0+eps1;
h0:=abs(2*eps1)/mm; end; if func(xk)= 0 then begin x:=xk; goto 21; end; x:=xk0+ee*h0+eps1;
for i:= 1 to 2 do begin z:=x+i*h; if func(x) >= func(z) then goto 22; end;
for i:= 1 to 2 do begin z1:=x-i*h; if func(x) >= func(z1) then goto 22; end;
if abs(aaa-x)<=1e-20 then goto 22;
21: writeln (' ', x,' ', func(x)); aaa:=x;
kk:=kk+1; rex[kk]:=x;
22: k:=k+1 end; x0:=x0 + hh end;
end;
begin
writeln (' ':12,'Приближения корней'); writeln; writeln;
x00:=-320; x11:=320; eps0:=0.00049; h:=eps0/43; eps00:=eps0;
ident(x00,x11,eps0, h); writeln; writeln; writeln;
writeln (' ':12,'Уточнения корней'); writeln; writeln;
eps0:=eps0/10; h:=eps0/43;
For kk1:=1 to kk do
begin x00:=rex[kk1]-eps00; x11:=rex[kk1]+eps00; ident(x00,x11,eps0, h); end;
readln;
end.
Результат работы программы:
Приближения корней
-1.00000000000000E+0002 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
4.00070000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00010000000000E+0000 0.00000000000000E+0000
7.00000000000000E+0000 0.00000000000000E+0000
8.00000000000000E+0000 0.00000000000000E+0000
9.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0001 0.00000000000000E+0000
1.10000000000000E+0001 0.00000000000000E+0000
1.20000000000000E+0001 0.00000000000000E+0000
1.30000000000000E+0001 0.00000000000000E+0000
1.40000000000000E+0001 0.00000000000000E+0000
1.50000000000000E+0001 0.00000000000000E+0000
1.60000000000000E+0001 0.00000000000000E+0000
1.70000000000000E+0001 0.00000000000000E+0000
1.80000000000000E+0001 0.00000000000000E+0000
1.90003000000000E+0001 0.00000000000000E+0000
2.20000000000000E+0001 0.00000000000000E+0000
2.30000000000000E+0001 0.00000000000000E+0000
2.10000000000000E+0002 0.00000000000000E+0000
Уточнения корней
-1.00000000000000E+0002 0.00000000000000E+0000
2.00000000000000E+0000 0.00000000000000E+0000
3.00000000000000E+0000 0.00000000000000E+0000
4.00070000000000E+0000 0.00000000000000E+0000
4.00080000000000E+0000 0.00000000000000E+0000
5.00000000000000E+0000 0.00000000000000E+0000
6.00010000000000E+0000 0.00000000000000E+0000
6.00020000000000E+0000 0.00000000000000E+0000
7.00000000000000E+0000 0.00000000000000E+0000
8.00000000000000E+0000 0.00000000000000E+0000
9.00000000000000E+0000 0.00000000000000E+0000
1.00000000000000E+0001 0.00000000000000E+0000
1.10000000000000E+0001 0.00000000000000E+0000
1.20000000000000E+0001 0.00000000000000E+0000
1.30000000000000E+0001 0.00000000000000E+0000
1.40000000000000E+0001 0.00000000000000E+0000
1.50000000000000E+0001 0.00000000000000E+0000
1.60000000000000E+0001 0.00000000000000E+0000
1.70000000000000E+0001 0.00000000000000E+0000
1.80000000000000E+0001 0.00000000000000E+0000
1.90003000000000E+0001 0.00000000000000E+0000
1.90002000000000E+0001 0.00000000000000E+0000
2.20000000000000E+0001 0.00000000000000E+0000
2.30000000000000E+0001 0.00000000000000E+0000
2.10000000000000E+0002 0.00000000000000E+0000
2.10000100000000E+0002 0.00000000000000E+0000
Программа даст правильный результат при любом первичном радиусе локализации от 0.49 до «сколь угодно» малого, но при этом может нарушаться порядок вывода данных, или программа замедлится. Отступ в обе стороны от первично идентифицированных корней всегда должен выполняться на первичный радиус. Вторичный радиус локализации можно взять «произвольно» меньшим eps0/10 (=0.000049), но это замедлит выполнение программы.
При соответственных параметрах программа примера 7 инвариантно идентифицирует область корней, сами корни полинома, может использоваться для их уточнения. Аналог программы применим для идентификации всех нулей и локальных экстремумов функции одной переменной в произвольной области. В этом легко убедиться, задав на входе программы ITERPROCEDURE функцию, в частности из числа приведенных выше, скорректировав при необходимости условия приближения к нулю, указав соответствующие параметры и область поиска.
Заключение
Изложено инвариантное построение программ для нахождения всех нулей и экстремумов функций одной переменной в произвольных границах области их расположения без локализации начальных приближений. Построение основано на устойчивых адресных сортировках и позволяет идентифицировать искомые величины с точностью до формата представления данных, что наряду с преобразованием к максимально параллельной форме составляет отличие предложенного метода от известных [11–13]. Метод распространяется на обработку сигналов, изображений, временных рядов, на информационный поиск. В частности, применение к распознаванию изображений отражено в [14], определение экстремальных признаков тенденций на графиках валютных котировок – в [15]. Используемые сортировки параллельны, на этой основе предложенные алгоритмы преобразуется к максимально параллельной форме.
Библиографическая ссылка
Ромм Я.Е. ИДЕНТИФИКАЦИЯ НУЛЕЙ И ЭКСТРЕМУМОВ ФУНКЦИЙ НА ОСНОВЕ СОРТИРОВКИ С ПРИЛОЖЕНИЕМ К АНАЛИЗУ УСТОЙЧИВОСТИ. I. СЛУЧАЙ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ // Современные наукоемкие технологии. – 2020. – № 6-1. – С. 79-97;URL: https://top-technologies.ru/ru/article/view?id=38075 (дата обращения: 21.11.2024).