В настоящее время внедрение методов искусственного интеллекта становится все более актуальным в коммерческих и научных сферах. С целью оптимизации бизнес-процессов современные компании нуждаются в детальном статистическом анализе. Одним из релевантных вопросов для предпринимателей является прогнозирование их дохода на некоторое время вперед. На текущий момент существует множество решений, основанных на анализе предпринимательской деятельности [1–3]. Однако при задании определенных условий требуется наиболее подходящее решение, которое целиком и полностью будет соответствовать конкретному бизнес-процессу. Таким образом, данная работа ориентирована на решение проблемы прогнозирования дохода при открытии новой точки торговой сети. В ситуации выбора прибыльного месторасположения предприниматель учитывает нахождение других собственных функционирующих торговых точек, а также ряд условий, описывающих предполагаемое месторасположение. В ситуации неизвестности человек опирается на свою интуицию и ограниченное количество информации. В данной работе предполагается использовать подходы интеллектуального анализа данных для принятия решения о выборе будущей торговой точки, в частности прогнозирование выручки в условиях оценки уже существующих торговых точек. Имеющиеся торговые точки характеризуются рядом признаков, которые так или иначе могут отразиться на рентабельности месторасположения. Таким образом, в данной задаче будут учитываться геопространственные данные и конкретные характеристики каждого месторасположения.
В работе [1] авторы для оценки месторасположения вводят простую линейную регрессию, затем множественную регрессию и после описывают алгоритм нейронной сети, который применяется на розничном наборе данных из «Google Places API».
Ранее задача прогнозирования доходов розничной торговли была исследована в работах [3, 4].
Авторы работы [3] используют пространственно-временную эвристику с целью предсказать «идеальное» месторасположение торговой точки, которое в конечном итоге приведет к увеличению прибыли компании. В данной работе экспериментальный набор данных представлял собой объединение демографических и экономических данных, а сам подход состоял из двух этапов: машинное обучение и применение эконометрических методов. В работе [4] авторы уже описывали подход, в котором возможно рассчитать предполагаемую выручку торговой точки медицинской сети. Помимо этого, ими была описана диаграмма информационной системы, в которой одной из ее частей являлся модуль, выполняющий расчет предполагаемой выручки. Однако в данной работе авторы с целью уменьшения ошибки предсказания предложили иной подход к решению задачи предсказания выручки.
Область машинного обучения предоставляет широкий выбор алгоритмов интеллектуального анализа данных, реализация которых помогает решать теоретические и практические задачи. Примерами таких задач являются: отбор значимых признаков, рекомендации, прогнозирование, кластеризации, классификация и пр. [5, 6]. В данной работе будет описан ряд шагов, включающий предобработку данных, обучение математических моделей и выбор релевантной модели прогнозирования. Относительно шага предобработки данных будет выполнена операция шкалирования. Обучение математической модели реализовано с помощью подходов: лассо, гребневой регрессии и деревьев решений. В результате данной работы будет представлена математическая формула, описывающая поведение выхода модели (прибыль торговой точки), и набор значимых признаков с подобранными коэффициентами, влияющими на этот выход.
Материалы и методы исследования
Для реализации эксперимента были проанализированы данные определенной торговой сети медицинских товаров. Количество признаков, влияющих на результат выручки, составляет 121 единицу, а торговая сеть располагает 67 розничными торговыми точками. Полученные признаки характеризуют каждую торговую розничную точку одной сети: площадь помещения, количество ступенек, наличие окна, количество касс, количество рабочих часов, тип торгового помещения: отдельно стоящее, или торговый центр, или находится в лечебном учреждении.
К геоинформационным данным относятся следующие признаки: количество квартир; средний возраст зданий; количество остановок общественного транспорта; количество дорожных развязок; количество станций метро; размер трафика в метро; количество супермаркетов; количество торговых центров; количество конкурентов; количество магазинов и пр.
Особенностью геоинформационных данных является то, что каждый признак имеет дополнительный атрибут, выраженный в расстоянии, а именно радиусе. Таким образом, от предполагаемой торговой точки откладывается радиус в 100, 200, 300, 400, 500 и 800 м, в данном радиусе измеряется количество тех или иных объектов, соответствующих вышеописанных признакам. Примером может служить признак «transport_stops_200», который обозначает количество транспортных остановок в радиусе 200 м от предполагаемой торговой точки.
Программная реализация эксперимента включает в себя три основных шага, на первом из них происходит предобработка данных. На втором шаге в ходе вычислительного эксперимента определяется оптимальное количество признаков, влияющих на доход торговых точек, и на последнем шаге происходят обучение моделей и сравнение результатов предсказания моделей относительно их ошибок.
В ходе предобработки данных выбросы были сглажены с помощью правила межквартильных размахов. Из-за малого количества точек вместо удаления точки с выбросами сглаживание происходило с помощью значений 0,05 и 0,95 квантиля. Помимо этого, была применена операция шкалирования по причине того, что все признаки имели разный диапазон значений, в конечном счете все значения были приведены к диапазону от 0 до 1. Значения категориальных признаков (количество кассиров, тип здания) приводились к значениям 0 и 1, так как они являются бинарными и нет необходимости вводить фиктивные переменные. Неинформативные признаки были удалены с помощью метода «near zero-variance predictors» [7]. Признаки, которые имеют малые колебания, были исключены. Например, если признак принимает значение 0 или 1 и при этом в 95 % случаях он принимает только значение 1, то он считается неинформативным. Также для того, чтобы исключить экспоненциальную зависимость, была использована трансформация бокса-кокса [8].
Особенный интерес для анализа представляют интерпретируемые модели. Важная особенность этой задачи состоит в том, что данные содержат более 100 признаков и всего 67 кортежей значений. В этом случае обучать обычную линейную регрессию не имеет смысла, по этой причине были обучены линейные модели с регуляризацией, а именно: гребневая регрессия [9] и регрессия лассо [10]. Данные модели имеют параметр регуляризации λ – гиперпараметр, который был подобран путем поиска перебором по значениям {400, 200, 100, 50, 40, 30, 20, 10, 5, 2, 1, 0.1, 0.01, 0.001, 0.0001, 0}. Для выбора оптимальной модели использовалась процедура эмпирического оценивания обобщающей способности алгоритмов – скользящий контроль по отдельным объектам. В качестве меры ошибки применялась средняя абсолютная ошибка. Для добавления нелинейности данных был использован алгоритм построения дерева решений M5 [11] с линейной регрессией на узлах. В качестве линейной регрессии использовалась лассо-регрессия для уменьшения количества признаков и предотвращения переобучения.
Результаты исследования и их обсуждение
В табл. 1 представлены результаты построения регрессии лассо и гребневой регрессии. Как видно, обе эти модели плохо описывают данные. Вероятно, простая линейная регрессия не способна описать зависимость между спрогнозированным доходом и признаками торговой точки.
Таблица 1
Результаты сравнения точности прогноза моделей
|
Модель |
MAE |
MAPE |
Процент точек, где точность более 80 |
|
Лассо |
453,46 |
40,14 % |
33,3 % |
|
Гребневая |
523,2 |
51,66 % |
32,0 % |
|
Дерево M5 |
249,34 |
19,23 |
71,32 % |
При реализации алгоритма «M5» первым признаком, по которому построилось дерево, было количество квартир в радиусе 500 м. Если его нормированное значение больше 0,5, то прогноз осуществляется по формуле:
income_rate = – 0.28*avg_buildings_age_100 – 0.04*transport_stops_500 + 0.1*wifi_traffic_100 + 0.09*malls_300 – 0.2*rubric_360_500 + 0.18*rubric_399_300 + 0.05*pharmacies_100 + 0.01*street_retail_200 + 0.01*competitors_400
Если значение было меньше 0,5, то для прогноза использовалась формула:
income_rate = + 0.07*transport_stops_300 + 0.06*transport_stops_400 + 0.18*transport_stops_500 + 0.04*supermarkets_300 + 0.01*malls_ 100 + 0.04*malls_800 + 0.07*rubric_399_400 + 0.17*rubric_410_200 + 0.1*rubric_418_800
Интерпретация наименований признаков модели представлена в табл. 2. На рис. 1 показана матрица корреляции, где цветом обозначен переход от положительной корреляции к отрицательной. Стоит отметить, что на размер дохода торговых точек (признак «income_rate») влияют признаки «avg_buildings_age_100» и «rubric_360_500» в большей степени, что и было доказано при вычислении формулы модели, отражено в коэффициентах выражения. Можно заметить, что и сами признаки, влияющие на выход модели (признак «income_rate»), коррелируют между собой, это видно на примере признаков «rubric_360_500» и «transport_stops_400», а также «rubric_360_500» и «transport_stops_300».
Таблица 2
Интерпретация наименований признаков моделей
|
Наименование признака в БД |
Перевод |
Наименование признака в БД |
Перевод |
|
income_rate |
Доходность торговой точки |
pharmacies |
Количество аптек |
|
avg_buildings_age |
Средний возраст зданий |
street_retail |
Количество точек розничной торговли |
|
transport_stops |
Количество остановок общественного транспорта |
competitors |
Количество конкурентов |
|
wifi_traffic |
Проходимость торговой точки |
supermarkets |
Количество продовольственных магазинов |
|
malls |
Количество торговых центров |
rubric_360, 399, 410, 418 |
Количество медицинских учреждений (поликлиник, больниц, стоматологий, медицинских центров и т.д.) |
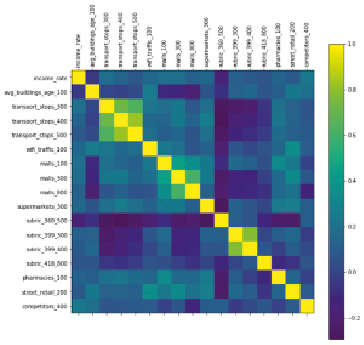
Рис. 1. Корреляционная матрица признаков моделей
Результаты прогноза модели «M5» приведены на рис. 2. Звездочками показаны настоящие значения прибыльности точек, упорядоченные в порядке возрастания.
Красной линией показан прогноз для соответствующих точек. Для каждой точки модель переобучалась без использования этой точки, и только после этого делался прогноз. Следовательно, модель эту точку еще «не видела». Как видно, средняя относительная ошибка прогноза стала меньше в несколько раз. Более глубокие модели показали ошибку на скользящем контроле более чем M5. При этом интерпретировать модель довольно легко. Если количество квартир в радиусе 500 м больше среднего, то имеют сильное отрицательное влияние возраст зданий и рубрика «rubric_360», зато положительно влияет рубрика «rubric_399» в радиусе 300 м. Также положительно влияют «wifi_traffic» и количество торговых центров в радиусе 300 м. Если количество квартир в радиусе 300 м меньше среднего, то на доходность торговой точки положительно влияют «rubric_410» и «rubric_418». Также положительно влияет количество транспортных остановок в радиусе 500 м, что логично, так как, если квартир мало, для точки важно, есть ли рядом остановки, на которые люди могут приезжать.
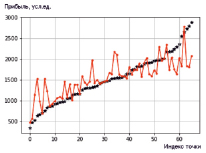
Рис. 2. Результат прогноза модели М5
Заключение
Как можно заметить, модель 5 раз завысила результат предсказания доходности торговых точек с малой прибылью и в несколько раз завысила прогноз для торговых точек со средней прибылью, занизила прибыльность торговых точек с большой прибыльностью. Стоит отметить, что на точность прогноза могут влиять и другие признаки, которые не были охвачены данным экспериментом, например человеческий фактор – оценка качества работы продавцов. Обзор работ по данной тематике позволяет говорить о том, что набор признаков, который анализируется специалистами по работе с данными, может включать в себе как геопространственные, так и данные экономических показателей, описывающих возможную привлекательность торговой точки или места предоставления разного рода услуг. Очень важно отобрать признаки, которые способны в той или иной мере повлиять на результат предсказания, причем не стоит пренебрегать тематикой сферы торговой сети. Таким образом, поиск признаков, описывающих привлекательность торговой точки, остается одной из актуальных задач для исследователей. Кроме того, на результат предсказания могут повлиять специфика торговой сети и качество предоставляемых услуг. В будущем авторы планируют расширять текущую работу за счет поиска признаков, описывающих данную предметную область, в частности фармацевтическую отрасль. Вследствие этого полученные релевантные признаки смогут оказать положительное влияние на результат прогноза, а именно повлиять на уменьшение ошибки.
Библиографическая ссылка
Пахомова К.И., Пересунько П.В., Виденин С.А. ПРОГНОЗИРОВАНИЕ ВЫРУЧКИ ПРЕДПОЛАГАЕМОЙ ТОРГОВОЙ ТОЧКИ СЕТИ МЕДИЦИНСКИХ ТОВАРОВ НА ОСНОВЕ ГЕОИНФОРМАЦИОННЫХ ДАННЫХ // Современные наукоемкие технологии. 2020. № 6-1. С. 74-78;URL: https://top-technologies.ru/ru/article/view?id=38074 (дата обращения: 14.02.2026).
DOI: https://doi.org/10.17513/snt.38074



