Одноцилиндровые двигатели используются на мотоциклах, мотоблоках для средств малой механизации, а также для многоцелевого назначения. В таких двигателях возникает проблема уравновешивания центробежных сил инерции неуравновешенных вращающихся масс кривошипа, а также сил инерции первого и второго порядков, вызванных возвратно поступательным движением масс поршневой группы. Обычно в таких двигателях уравновешивают только центробежные силы вращающихся масс и силы инерции первого порядка [1, 2]. Если центробежные силы инерции вращающихся масс кривошипа уравновешиваются противовесами на продолжении щек коленчатого вала, то использование таких противовесов для уравновешивания сил инерции первого порядка просто переводит их из вертикальной плоскости в горизонтальную [3–5]. Такой способ уравновешивания используется на некоторых мотоциклетных двигателях.
Кроме того, для снижения виброактивности одноцилиндрового двигателя широко используется дополнительный уравновешивающий вал, который располагается справа от коленчатого вала по ходу его вращения [5–7]. Привод дополнительного вала осуществляется через шестерню от коленчатого вала. На этом дополнительном валу устанавливаются противовесы, а такие противовесы устанавливаются на коленчатом валу. Поскольку коленчатый и дополнительный валы вращаются в противоположные стороны, то вертикальная составляющая сил инерции двух противовесов будет складываться и тем самым уравновешивать силу инерции первого порядка [1, 2]. Горизонтальные составляющие направлены в противоположные стороны и уравновешивают друг друга. Однако от вертикальной составляющей центробежной силы инерции сил противовеса на дополнительном валу возникает момент, который дополнительно нагружает опоры двигателя [1, 2].
Цель исследования: определить влияние дополнительного момента на опоры двигателя, наиболее рациональное место установки по отношению к коленчатому валу, на каких участках поворота коленчатого вала он направлен против опрокидывающего момента, а на каких участках – складывается с ним, тем самым повышает виброактивность одноцилиндрового двигателя. Кроме того, проанализируем, каким образом влияет расположение дополнительного вала на габаритные размеры самого двигателя.
Материалы и методы исследования
Представим, что уравновешивающий вал располагается справа от коленчатого вала (по направлению вращения) так, что прямая, соединяющая оси коленчатого вала и дополнительного, располагается под углом α от вертикальной оси цилиндра (рис. 1). Если расстояние между осями коленчатого вала O и дополнительного – O1 равно l, то проекция его на горизонтальную ось (ось x) равна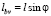 
, а на вертикальную (ось y) – 
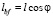(рис. 1).
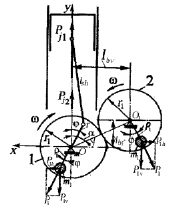
Рис. 1. Схема уравновешивания сил инерции первого порядка в одноцилиндровом двигателе с дополнительным валом
На коленчатом валу установлена шестерня 1, которая приводит во вращение шестерню 2, расположенную на дополнительном валу. Шестерни 1 и 2 содержат на расстоянии ρ1 от оси вращения противовесы массой m1 и установлены так, что при любом повороте кривошипа положение радиуса ρ1 полностью определятся углом поворота кривошипа.
Шестерни 1 и 2 вращаются в противоположные стороны, и при этом при вращении масс m1 возникают силы инерции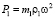 
. Проекции этих сил на ось y равны 
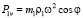и складываются, тем самым уравновешивая силу инерции первого порядка
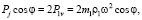
откуда масса m1 определяется как
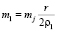. (1)
Здесь mj – масса деталей, совершающих возвратно-поступательное движение.
Вместе с тем равнодействующая двух сил P1v составляет пару с силой Pj, момент которой можно определить как (рис. 1);
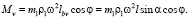
Решение получено из условия, что в соответствии с правилами теоретической механики воздействие сил P1 на систему не изменится, если их перенести в точки O и O1. Заметим, что решение может быть получено, если найти момент сил P1v относительно точки O (рис. 1, положительный момент выбирается, если его направление совпадает с направлением вращения коленчатого вала):
,
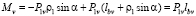или
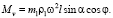(2)
Составляющие силы P1 по горизонтали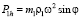 
(рис. 1) направлены противоположно друг другу и составляют пару сил с моментом Mh (знак плюс выбираем аналогично по направлению вращения коленчатого вала):
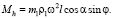(3)
Оба момента воздействуют на опоры двигателя, как и опрокидывающий момент Mup, который, как известно, равен крутящему моменту Mtd, но имеет противоположное направление, т.е.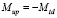 
[1].
Суммарный момент от действия силы инерции на дополнительном валу равен
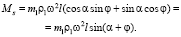(4)
Поскольку возникающий дополнительный момент Ms может усиливать опрокидывающий момент Mup или, наоборот, уменьшать действие его опоры двигателя, то в связи с этим целесообразно провести исследования наиболее целесообразного расположения дополнительного вала. Заметим, что опрокидывающий момент Mup всегда равен и противоположно направлен крутящему моменту двигателя Mtd.
В качестве оценочных показателей рационального расположения дополнительного вала примем:
– угол α между осью цилиндра и прямой, соединяющей оси валов коленчатого O и дополнительного – O1 (рис. 1);
– среднее значение дополнительного момента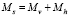 
при изменении угла α;
– изменение среднего значения опрокидывающего момента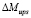 
при наличии дополнительного вала;
– изменение размаха суммарного опрокидывающего и дополнительного моментов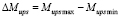 
;
– изменение габаритных размеров двигателя при различных положениях дополнительного вала.
Проведем исследование по принятым оценочным показателям численно для реального одноцилиндрового дизеля с определением необходимых масс противовесов, так как в общем виде по зависимости (4) определить это невозможно.
Численный расчет проведем для дизеля ТМЗ-650Д (1Ч9,55/9,2) номинальной мощности 12 кВт при частоте вращения коленчатого вала n = 3600 мин-1.
Для расчета сил инерции движущихся деталей кривошипно-шатунного механизма (КШМ) дизеля ТМЗ-650Д массы их определялись в результате взвешивания в лаборатории кафедры «Тепловые двигатели и энергетические установки» ВлГУ, а также путем анализа чертежей по трехмерной модели, выполненной с помощью программного комплекса SolidWorks Simulation. Результаты взвешивания и расчетов приведены в табл. 1. Поскольку уравновешивание центробежных сил вращающихся масс кривошипа – задача известная, то в данном случае рассматривается только уравновешивание только сил инерции первого порядка.
Определим силу инерции первого порядка Pj1 на режиме номинальной мощности (n = 3600 мин-1; ω = 376,8 1/с):
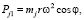
где mj = mp + mpp + mpr + m1 = 1,316 кг (табл. 1) – массы, совершающие возвратно-поступательное движение (поршень, поршневой палец, поршневые кольца, часть массы шатуна, отнесенная к оси поршневого пальца); r = 0,046 м – радиус кривошипа.
Максимальная сила инерции первого порядка Pj1, действующая в плоскости, проходящей через ось коренных шеек и ось цилиндра (рис. 1), равна
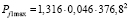= 8594,8 Н.
Она должна быть уравновешена вертикальными составляющими центробежных сил инерции двух противовесов массой m1, установленных на радиусе ρ1 = 0,046 м от оси вращения. В соответствии с зависимостью (1) определяем
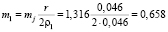кг.
Максимальная сила инерции при вращении противовеса массой m1 = 0,658 кг на радиусе ρ1 = 0,046 м равна
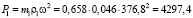Н.
Таблица 1
Массы деталей КШМ дизеля ТМЗ-650Д
|
Наименование детали или ее составной части |
Массы деталей mi, кг |
|
1. Поршень mp |
0,645 (0,640) |
|
2. Поршневой палец mpp |
0,241 |
|
3. Поршневые кольца mpr |
0,1 |
|
4. Шатун с вкладышами msh |
0,950 ± 0,015 |
|
5. Часть массы шатуна, отнесенная к оси поршневого пальца m1 |
0,33 |
По программе, разработанной на кафедре «Тепловые двигатели и энергетические установки», был проведен динамический расчет дизеля ТМЗ-650Д и определено значение крутящего и опрокидывающего момента в зависимости от угла поворота коленчатого вала. Результаты расчета приведены в табл. 2.
В табл. 2 Mtd, Н·м – крутящий момент двигателя на режиме номинальной мощности. Для того чтобы определить, как влияет расположение дополнительного вала относительно коленчатого на величину дополнительного момента Ms (усиливает или уменьшает величину опрокидывающего момента), определим по зависимости (4) величину и направление Ms. Примем знак момента положительным, если его направление совпадает с направлением вращения коленчатого вала.
Результаты расчетов приведены в табл. 3. Поскольку крутящий момент двигателя Mtd и, соответственно, равный ему и противоположно направленный опрокидывающий момент Mup имеют относительно большие значения только в конце такта сжатия и примерно до середины такта расширения, то для того, чтобы расчет был корректным, значения Ms подсчитывались через 5? ПКВ. Для экономии места в табл. 3 приведены результаты расчета через 30° ПКВ, хотя средние значения определялись через 5° ПКВ.
Результаты исследования и их обсуждение
Проанализируем полученные расчетным путем результаты. В соответствии с зависимостью (4) дополнительный момент изменяется по синусоидальному закону, а угол α, определяющий положение дополнительного вала относительно коленчатого, выступает в качестве начального. Поэтому, кроме положения дополнительного вала при α = 0 (чистая синусоида) и α = 180° (косинусоида), для момента Ms можно подсчитать среднее значение.
Таблица 2
Значение крутящего и опрокидывающего момента по данным динамического расчета
|
φ°, ПКВ |
Mtd, Н·м |
Mup, Н·м |
φ°, ПКВ |
Mtd, Н·м |
Mup, Н·м |
φ°, ПКВ |
Mtd,r, Н·м |
Mup, Н·м |
|
0 15 30 45 60 75 90 105 120 135 150 165 180 195 210 225 |
0 –90 –140 –130 –72 5 67 97 96 76 49 24 0 –0,73 –0,154 –79 |
0 90 140 130 72 –5 –67 –97 –96 –76 –49 –24 0 0,73 0,154 79 |
240 255 270 285 300 315 330 345 360 375 390 405 420 435 450 465 |
–106 –122 –96 –80 –28 –44 –155 –315 0 893 798 503 360 290 261 227 |
106 122 96 80 28 44 155 315 0 –893 –798 –503 –360 –290 –261 –227 |
480 495 510 525 540 555 570 585 600 615 630 645 660 675 690 705 720 |
188 135 82 37 0 30 –57 –97 –111 –129 –88 –29 –56 –122 –126 –88 0 |
–188 –135 –82 –37 0 –30 57 97 111 129 88 29 56 122 126 88 0 |
|
Средние значения Mtd и Mup, Н·м |
37,9 |
–37,9 |
||||||
Расчетные значения дополнительного момента Ms, Н·м
|
φ α° |
Момент от дополнительных противовесов, массой mt = 0,658 кг |
Момент Mup, Н·м |
||||||||||
|
0 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
||
|
0 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
|
30 |
215,2 |
372,73 |
430,38 |
372,73 |
215,19 |
0 |
–215,2 |
–372,73 |
–430,38 |
–372,73 |
–215,19 |
–0,01 |
|
60 |
372,73 |
430,38 |
372,73 |
215,2 |
0 |
–215,19 |
–372,73 |
–430,38 |
–372,73 |
–215,2 |
0,01 |
215,19 |
|
90 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
0 |
215,2 |
372,72 |
|
120 |
372,73 |
215,19 |
0 |
–215,2 |
–372,73 |
–430,38 |
–372,73 |
–215,19 |
–0,01 |
215,2 |
372,73 |
430,38 |
|
150 |
215,2 |
0 |
–215,19 |
–372,73 |
–430,38 |
–372,73 |
–215,2 |
0,01 |
215,19 |
372,73 |
430,38 |
372,73 |
|
180 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
|
210 |
–215,2 |
–372,73 |
–430,38 |
–372,73 |
–215,19 |
0 |
215,2 |
372,73 |
430,38 |
372,73 |
215,19 |
0,01 |
|
240 |
–372,73 |
–430,38 |
–372,73 |
–215,2 |
0 |
215,19 |
372,73 |
430,38 |
372,73 |
215,2 |
–0,01 |
–215,19 |
|
270 |
–430,39 |
–372,72 |
–215,2 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
|
300 |
–372,73 |
–215,19 |
0 |
215,2 |
372,73 |
430,38 |
372,73 |
215,19 |
0,01 |
–215,2 |
–372,73 |
–430,38 |
|
330 |
–215,2 |
0 |
215,19 |
372,73 |
430,38 |
372,73 |
215,2 |
–0,01 |
–215,19 |
–372,73 |
–430,38 |
–372,73 |
|
360 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
|
390 |
215,2 |
372,73 |
430,38 |
372,73 |
215,19 |
0 |
–215,2 |
–372,73 |
–430,38 |
–372,73 |
–215,19 |
–0,01 |
|
420 |
372,73 |
430,38 |
372,73 |
215,2 |
0 |
–215,19 |
–372,73 |
–430,38 |
–372,73 |
–215,2 |
0,01 |
215,19 |
|
450 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
0 |
215,2 |
372,72 |
|
480 |
372,73 |
215,19 |
0 |
–215,2 |
–372,73 |
–430,38 |
–372,73 |
–215,19 |
–0,01 |
215,2 |
372,73 |
430,38 |
|
510 |
215,2 |
0 |
–215,19 |
–372,73 |
–430,38 |
–372,73 |
–215,2 |
0,01 |
215,19 |
372,73’ |
430,38 |
372,73 |
|
540 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
|
570 |
–215,2 |
–372,73 |
–430,38 |
–372,73 |
–215,19 |
0 |
215,2 |
372,73 |
430,38 |
372,73 |
215,19 |
0,01 |
|
600 |
–372,73 |
–430,38 |
–372,73 |
–215,2 |
0 |
215,19 |
372,73 |
430,38 |
372,73 |
215,2 |
–0,01 |
–215,19 |
|
630 |
–430,39 |
–372,72 |
–215,2 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
|
660 |
–372,73 |
–215,19 |
0 |
215,2 |
372,73 |
430,38 |
372,73 |
215,19 |
0,01 |
–215,2 |
–372,73 |
–430,38 |
|
690 |
–215,2 |
0 |
215,19 |
372,73 |
430,38 |
372,73 |
215,2 |
–0,01 |
–215,19 |
–372,73 |
–430,38 |
–372,73 |
|
720 |
0 |
215,2 |
372,72 |
430,39 |
372,72 |
215,2 |
0 |
–215,2 |
–372,72 |
–430,39 |
–372,72 |
–215,2 |
|
Среднее значение Мsm, Н м |
0 |
8,61 |
14,91 |
17,22 |
14,91 |
8,61 |
0 |
–8,61 |
–14,91 |
–17,22 |
–14,91 |
–37,9 |
Таким образом, положительный знак (по направлению вращения) дополнительного момента Ms направлен против опрокидывающего момента Mup, а значит, он будет уменьшать величину Mup и тем самым уменьшит нагрузку на опоры двигателя. Из анализа первого оценочного параметра, принятого нами для выбора рационального расположения дополнительного вала, т.е. угла α, можно признать, что более рациональным является расположение уравновешивающего вала справа от коленчатого (вид с носка вала) по направлению вращения (рис. 1), т.е.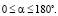 
Если дополнительный вал установить на другом участке, то суммарный момент 
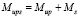будет увеличиваться, так как, когда 
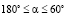, среднее значение дополнительного момента Msm < 0 (табл. 3), тем самым будет увеличена нагрузка на опоры двигателя.
Значение суммарного момента Mups (опрокидывающего и дополнительного) определяли, как обычно:
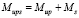. (5)
Графики изменения опрокидывающего момента Mup (кривая 1), дополнительного момента Ms (кривая 2) и суммарного Mups, определяемого по зависимости (5) (кривая 3), при двух значениях α = 45° приведены на рис. 2.
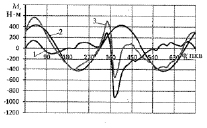
Рис. 2. Изменение моментов: опрокидывающего Mup (кривая 1), дополнительного Ms (кривая 2) и суммарного Mups (кривая 3) при α = 45°
Для анализа еще трех оценочных показателей: изменение среднего значения дополнительного момента Msm, изменение среднего значения суммарного опрокидывающего и дополнительного моментов Mupsm, а также размаха суммарного опрокидывающего и дополнительного моментов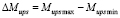 
приведено на рис. 3 и 4.
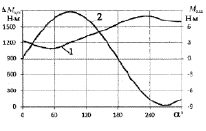
Рис. 3. Изменение размаха суммарного опрокидывающего и дополнительного моментов ΔMups (кривая 1) и среднего значения дополнительного момента Ms (кривая 2) в зависимости от угла α
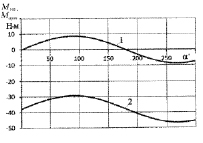
Рис. 4. Изменение среднего значения дополнительного момента Msm (кривая 1) и среднего значения опрокидывающего и дополнительного момента Mupsm (кривая 2) в зависимости от угла α
Проанализируем полученные результаты. Как следует из рис. 1, при увеличении угла α размаха суммарного опрокидывающего и дополнительного моментов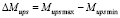 
увеличивается (кривая 1). При α = 240° эта величина достигает максимального значения 
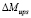= 1802 Н·м. В дальнейшем рост его немного замедляется, но все равно остается достаточно большим. В то же время среднее значение дополнительного момента Ms (кривая 2) в зависимости от угла α при α = 180° меняет знак на отрицательный, тем самым усиливает величину опрокидывающего момента и размаха 
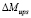. По сравнению с первым оценочным показателем можно значительно сузить изменения угла наклона α. Наиболее рациональным можно принять 
.
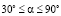Показанные на рис. 3 графики: изменение среднего значения дополнительного момента Msm (кривая 1) и среднего значения опрокидывающего и дополнительного момента Mupsm (кривая 2) в зависимости от угла α – показывают, что принятые нами ограничения угла α закономерны.
Среднее значение дополнительного момента Msm при угле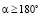 
принимает отрицательное значение, тем самым увеличивает величину опрокидывающего момента.
Что касается изменения габаритных размеров двигателя при различных положениях дополнительного вала, то, как следует из рис. 1, при всех значениях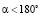 
в поперечном сечении габариты уменьшаются.
Заметим, что для уменьшения расстояния от оси вращения до центра масс противовесов обычно выполняют балансирные валы, средняя часть которых имеет проточку, как показано на рис. 5.
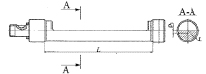
Рис. 5. Балансирный вал
При такой конструкции дополнительного вала значительно уменьшаются габариты двигателя. Такие валы использовались для уравновешивания сил инерции первого порядка на двигателях ВАЗ-11113.
Выводы
На основе численного расчета сил инерции первого порядка для одноцилиндрового двигателя и их уравновешивания с помощью дополнительного уравновешивающего вала показано, что целесообразно располагать такой вал справа от оси коленчатого вала (по направлению вращения) так, чтобы угол наклона линии, соединяющей оси валов коленчатого и дополнительного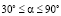 
.
Библиографическая ссылка
Гоц А.Н., Клевцов В.С. ВЫБОР РАЦИОНАЛЬНОЙ СХЕМЫ УРАВНОВЕШИВАНИЯ ОДНОЦИЛИНДРОВОГО ДВИГАТЕЛЯ // Современные наукоемкие технологии. – 2020. – № 6-1. – С. 37-43;URL: https://top-technologies.ru/ru/article/view?id=38068 (дата обращения: 03.12.2024).