Упрочнение сменных деталей металлургического оборудования, работающих при высокотемпературных видах износа, успешно осуществляется электрошлаковой наплавкой (ЭШН) композиционными материалами (КМ) на основе спечённого твёрдого сплава типа ТН 20. С целью повышения износостойкости сменных деталей, упрочнённых ЭШН КМ, выполнено математическое моделирование поведения твёрдых частиц в высокотемпературной зоне шлаковой ванны. В частности, определены основные факторы моделирования, воздействующие на износостойкость: скорость движения шлакового потока и твёрдых частиц, время пребывания и нагрев твёрдых частиц в высокотемпературной шлаковой зоне, влияние нагрева твёрдых частиц на износостойкость наплавленных деталей. В процессе моделирования температурное поле шлаковой ванны измеряли параллельно двумя способами: прямым – непосредственно термопарами, и косвенным – с использованием устройства для оценки удельной электропроводности жидких сред. Второй способ измерения температуры основан на известной температурной зависимости удельной электропроводности используемых расплавов флюса для ЭШН, которую замеряли разработанным устройством в процессе эксперимента. Взаимосвязанное численное описание теплового поля шлаковой ванны осуществляли с помощью методики, основанной на способе численного сеточного моделирования с использованием оператора Лапласа ∇2T = ∂2T/∂y2 + ∂2T/∂z2. Определение температурных зон шлаковой ванны, нагрева и движения твёрдых частиц в шлаковом потоке осуществляли с помощью математического моделирования параметров ЭШН в каждом опыте полнофакторного эксперимента. Комплексная программа моделирования температурного поля шлаковой ванны направлена: на регулирование температурного режима, предотвращающего образование сложнолегированных структур на поверхности раздела твёрдая частица – матрица; на снижение термических напряжений и деформаций; на повышение высокотемпературной износостойкости упрочнённых деталей.
В области наплавки композиционных материалов (КМ) на основе твёрдых карбидных частиц имеется достаточное количество экспериментальных данных, разработанных авторами различных школ: СибГИУ [1–3], ВолгГТУ [4–6], ИС им. Е.О. Патона [7–9], так и зарубежных [10–12]. Однако практически отсутствуют работы, исследующие процесс нагрева и взаимодействие твёрдых частиц с металлом-связкой, приводящих к образованию сложнолегированных структур в процессе наплавки. Прочность при высоких температурах и износостойкость КМ, упрочнённых твёрдыми частицами, как указывают авторы монографий [13–15], напрямую зависит от физических факторов: температуры нагрева твёрдых частиц в шлаковой ванне; размера частиц и расстояния между ними; протяжённости зоны сплавления; теплофизических свойств сплава-связки (матрицы) и твёрдых частиц, а также объёмной доли упрочняющей фазы. Поэтому, учитывая повышенную прочность спечённых твёрдых сплавов ТН 20 на изгиб и на сжатое σизг = 1,15-1,60, σсж = 3,5-4,5 ГПа, высокую микротвердость Нμ = 18,5-22,0 ГПа, наибольшую вязкость среди спечённых твёрдых сплавов KCU = 0,9-1,2 МДж/м2, хорошую смачиваемость металлами группы железа (угол смачивания 0 град) и повышенную жаропрочность и жаростойкость, в работе были использованы в качестве износостойкой твёрдой фазы КМ при электрошлаковой наплавке (ЭШН) спечённые твёрдые сплавы на основе карбида титана типа ТН 20 [2, 8, 16].
Для математического моделирования теплометрических параметров ЭШН КМ, обеспечивающих повышенную высокотемпературную износостойкость наплавленных деталей, установлены следующие цели:
- измерение удельной электропроводности и плотности тока ЭШН с целью моделирования температурного поля шлаковой ванны [1, 16, 17];
– исследование температурного поля ЭШН с использованием взаимосвязанного численного описания электротеплового поля с помощью методики, основанной на способе численного сеточного моделирования [1, 18, 19];
- построение зон распределения температуры шлаковой ванны, нагрева и движения твёрдых частиц в шлаковом потоке, с помощью математического моделирования, основанном на параметрах ЭШН в каждом опыте [1, 19, 20];
- использование скоростной киносъёмки движения твёрдых частиц в шлаковой ванне, с целью определения траектории движения, нагрева и времени пребывания твёрдых частиц в высокотемпературной зоне ЭШН [3, 21, 22].
Для разработки перспективных способов ЭШН КМ на основе спечённого твёрдого сплава типа ТН 20 необходимо изучить влияние параметров ЭШН на температурные поля шлаковой ванны, с целью регулирования нагрева и взаимодействия твёрдых частиц в матрице КМ. Это позволит разработать рациональные способы подачи твёрдых частиц в зону наплавки, определить опорные значения режимов ЭШН, установить приёмы управления технологическими процессами, предотвращающие растворение твёрдых частиц в матрице и образование сложнолегированных структур в КМ [3, 7, 23].
Материалы и методы исследования
Температуру в каждой точке шлаковой ванны можно моделировать с помощью удельной электропроводности шлака (по известной температурной зависимости), измеряемой в этой точке разработанным устройством. Устройство включает в себя датчик, источник напряжения Г на 100 мВ частотой 5 кГц, ламповый вольтметр V с диапазоном измеряемых напряжений до 100 мВ, универсальный амперметр A с диапазоном измеряемых токов 0,03...300 мА, переключатель П [1, 18, 19].
Моделирование температурного поля шлаковой ванны проводили с использованием экспериментально найденных краевых условий. Взаимосвязанное численное описание электрического и теплового, иначе электротеплового поля шлаковой ванны можно осуществить с помощью методики, основанной на способе численного сеточного моделирования. Учитывая нестационарный характер тепловых процессов при электрошлаковой наплавке КМ по слою шихты, и особенно при дозированной подаче твёрдых частиц в шлаковую ванну, при описании температурных полей в каждом сечении шлаковой ванны в предположении изотропности пространства за основу было взято уравнение теплопроводности на основе оператора Лапласа ∇2T = ∂2T/∂y2 + ∂2T/∂z2 [1, 17, 18].
Микротвердость КМ, в том числе отдельно матрицы и твёрдых частиц, измеряли в интервале температур 20–800 °С на установке ИМАШ-9-66, имеющей специальное устройство для такого измерения. Механические испытания на растяжение КМ проводили на установке ИМАШ-5С-69 «Киргизстан» для высокотемпературной металлографии и на установке Р-5, оборудованной печью с карборундовыми силитовыми нагревателями, что позволило проводить испытания в интервале температур 20–800 °С [23–25].
Результаты исследования и их обсуждение
При электрошлаковой наплавке (ЭШН) композиционных материалов (КМ) неплавящимся электродом используются в основном две основные схемы: по слою шихты и вертикальная наплавка [3, 9, 24]. В обоих случаях явление массопереноса в шлаковой ванне оказывает существенное влияние на температурное поле ЭШН и нагрев твёрдых частиц. Кроме того, при подаче твёрдых частиц типа ТН 20 через слой шлака массоперенос оказывает влияние на траекторию движения и нагрев частиц твёрдого сплава ТН 20 в высокотемпературной зоне, следовательно, вызывает интерес скорость движения частиц ТН 20 и расплава шлака как внутри, так и на свободной поверхности шлаковой ванны.
Теоретическое определение температуры квазистационарного теплового поля в каждой точке шлаковой ванны даже при неизменных параметрах ЭШН: объёме, удельной теплоёмкости, теплопроводности и массе шлака – задача весьма сложная. В процессе исследования температуру в каждом элементарном объёме шлаковой ванны измеряли параллельно двумя способами: прямым – посредством термопары, и косвенным – с использованием устройства для оценки удельной высокотемпературной электропроводности жидких сред. Установка датчика и подготовка к измерению при прямом и косвенном способах подобны, но имеются различия в конструкции измерительных устройств и в методике оценки температуры.
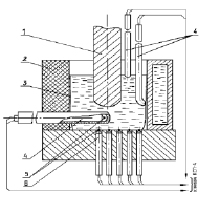
Рис. 1. Схема замера температур шлаковой ванны прямым способом при ЭШН: 1– неплавящийся графитовый электрод; 2 – графитовая заглушка; 3 – шлаковый гарнисаж; 4 – термопара в чехле; 5 – рабочий спай термопары; 6 – алундовая соломка
В первом случае основным датчиком служила вольфрам-рениевая термопара ВР-5/20, которая вставлялась в алундовый чехол с наружным диаметром 11 мм и толщиной стенки 3 мм. Датчик устанавливался горизонтально в подвижной графитовой заглушке толщиной 30 мм (рис. 1), причём рабочий конец термопары совмещался с центром изучаемого локального объёма шлаковой ванны, находившегося в её плоскости симметрии. Для повышения сохранности датчика в период выхода на заданные параметры ЭШН перед ним устанавливали дополнительный графитовый экран, который убирали в процессе стабилизации, и электрод возвращался в исходное положение. При этом в комплекте с термопарой использовали двухкоординатный потенциометр КСП-4 [1, 18, 20].
Температуру приграничных зон шлаковой ванны определяли прямым путём с помощью термопары ВР-5/20 и потенциометра КСП-4. Использование для этой цели косвенного способа часто невозможно, так как удельная электропроводность шлака при температурах приграничных слоёв ниже 1050 °С близка к нулю. При изучении приграничного с кристаллизатором слоя шлаковой ванны использовали кварцевый чехол с изогнутой под 45 град. концевой частью. Его опускали в ванну и в исследуемой точке утыкали концом в образующийся на стенке кристаллизатора гарнисаж. В детали сверлили сквозные отверстия, в которые снизу вставляли алундовые соломки с термопарами. Рабочие спаи термопар непосредственно контактировали с приграничным с деталью слоем шлака. При измерении температуры на границе шлак – воздух применяли кварцевый чехол, который вместе с термопарой погружали в шлак на 2...3 мм.
Косвенный способ измерения температуры в элементарном объёме шлаковой ванны основан на известной зависимости удельной электропроводности большинства расплавленных флюсов для ЭШН от температуры. Для каждого флюса соответствующая зависимость была получена разработанным датчиком в процессе эксперимента. Температуру в каждой точке шлаковой ванны можно косвенно оценивать по удельной электропроводности шлака, измеряемой в этой точке разработанным датчиком. Устройство включает в себя датчик, источник напряжения Г на 100 мВ частотой 5 кГц, ламповый вольтметр V с диапазоном измеряемых напряжений до 100 мВ, универсальный амперметр A с диапазоном измеряемых токов 0,03...300 мА, переключатель П. Датчик содержит 8 электродов из вольфрамовой проволоки диаметром 0,5 мм, которые введены в алундовые трубки с наружным диаметром 3,4 мм. Трубки помещены в кварцевый цилиндр, пространство между трубками и цилиндром заполнено спечённым алундовым порошком. На рабочем конце датчика электроды выступают из алундовых трубок на 1 мм, которые непосредственно контактируют с расплавом шлака. Один конец измерительной цепи (рис. 2) через переключатель П соединяется с вспомогательными (контрольными) электродами 3...8 датчика, размещёнными радиально вокруг основного (токового) электрода 1, который подсоединён ко второму концу токовой цепи. Под токовыми электродами 1 и 2 понимаются электроды, через которые протекает ток от источника питания устройства по цепи: источник > токовый электрод 1 > шлаковая ванна > токовый электрод 2 > амперметр А > выключатель В > источник.
Датчик погружали в шлаковую ванну так, чтобы выступающий из трубки рабочий конец токового электрода 1 совпадал с центром изучаемой локальной области. В момент измерения ток наплавки отключали, а тумблер устройства В включали. Последовательно измеряли падения напряжения U3...U8 между первым токовым электродом 1 и каждым из контрольных электродов 3...8. Дополнительно измеряли ток, протекающий через электроды 1–2. В промежутках между опытами включали повышенный ток наплавки для прогрева ванны до рабочих температур, чтобы режим наплавки соответствовал базовому: Iш = 350 А, Uш = 40 В. При достижении в форсированном режиме тока Iф.ш источник питания отключали и проводили новое параллельное измерение. Общее время всех замеров одним датчиком не превышало 3 мин.
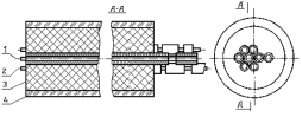
Рис. 2. Датчик и принципиальная схема для косвенного измерения температуры: П – переключатель; Р – потенциометр КСП-4; 1 – первый токовый электрод; 2 – второй токовый электрод; 3 – спечённый алундовый порошок; 4 – кварцевая трубка
После статистической обработки данных параллельных измерений удельную электропроводность локального объёма шлаковой ванны оценивали по формуле (1) [1, 18, 19]:
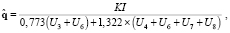[Ом-1, м-1] (1)
где K – константа устройства; I – ток, усреднённый по результатам параллельных опытов,
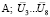– средние (по данным параллельных опытов) падения напряжения на участке ванны между первым токовым и соответственно одним из контрольных электродов 3...5, В.
Константу K предварительно определяли по данным контрольных измерений. Относительная погрешность косвенного способа измерения температуры, посредством замера удельной электропроводности разработанным датчиком при рабочих температурах до 1700 °С, составляет менее 5 %. Целесообразность комплексного измерения обусловливается наличием случайных помех, влияющих на оценки температуры. Для повышения достоверности результатов оценки, полученные прямым и косвенным способами, усредняли.
Математическое моделирование температурного поля шлаковой ванны проводили с использованием экспериментально найденных краевых условий. Взаимосвязанное численное описание теплового поля шлаковой ванны осуществляли с помощью методики, основанной на способе численного сеточного моделирования [1, 18, 19]. При моделировании начало координат располагается в центре дна прямоугольной шлаковой ванны с наплавленным слоем. Ось абсцисс X направлена по ходу движения, ось ординат У – поперёк детали, ось аппликат Z – вертикально вверх. Предполагается, что краевые условия задачи моделирования температурных полей шлаковой ванны соответствуют симметрии температуры относительно оси аппликат. Учитывая нестационарный характер тепловых процессов при наплавке КМ по слою шихты, и особенно при дозированной подаче твёрдых частиц в шлаковую ванну, при описании температурных полей в каждом сечении ванны в предположении изотропности пространства за основу было взято уравнение теплопроводности (2) [1, 17, 18]:
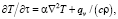(2)
где T = f (X, У, Z, t) – температура в точке шлаковой ванны с координатами, X-const, У, Z в момент времени τ; α = λ/(cρ) - средняя температуропроводность; λ и с – средние теплопроводность и удельная теплоёмкость; ρ - средняя плотность шлака в описываемом диапазоне температур; qv – плотность теплового потока в элементарном объёме; ∇2T = ∂2T/∂y2 + ∂2T/∂z2– оператор Лапласа, записанный для двумерной области в декартовой системе координат.
Поскольку основные параметры ЭШН ток и напряжение (Iн и Uн) становятся постоянными только при установившемся процессе, следовательно, их нельзя использовать как независимые, с этой целью был реализован план полнофакторного эксперимента 23 (табл. 1) с тремя независимыми параметрами: диаметр электрода Dэ, межэлектродный промежуток (расстоянием между электродом и наплавляемым слоем) Нм и сопротивление балластных реостатов Rб.
По результатам замеров при пятикратном дублировании опытов изучали распределение температур шлаковой ванны и наплавленного металла. Поиск значений коэффициентов Тr и Kr для каждого опыта осуществляли методом наименьших квадратов. Коэффициенты полученных уравнений рассматривались в качестве откликов эксперимента. В результате статистической обработки данных эксперимента найдены регрессионные зависимости, связывающие коэффициенты степенных уравнений с параметрами ЭШН [1, 18, 19]:
Т = Тг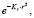
(3)
где r – радиальная координата, 0 < r < Bш.в.
Тr = 1238,2 – 18,5Н′мэ + 121,6Дэ′ – 7,7Rб′ – 41,4Н′мэ·Дэ′ – 73,3H′мэ·Rб′ + 23,3Дэ′·Rб′ + 47,3Н′мэ·Rб′·Дэ′; (4)
Kr = 2,1·10-4 + 0,03·10-4 Нмэ′ + 0,085·10-4 Дэ′ +0,055·10-4 Rб′ + 0,2·10-4 Hмэ′·Дэ′;
Дэ′ = (Дэ – 3,0)/0,5; Нмэ′ = (Нмэ – 1,1)/0,3;
Rб′ = (Rб – 0,115)/0,025. (5)
Подставляя параметры ЭШН в уравнения 3–5, можно оценить температуру шлаковой ванны и наплавленного КМ. Рассчитанные на ЭВМ кривые распределения температур на поверхности наплавленного КМ хорошо согласуются с экспериментальными данными, приведёнными на рис. 3. На основе этих данных температурное поле шлаковой ванны было описано рядом изотерм. Для нахождения параметров в промежуточных точках шлакового объёма между экспериментальными точками использовалась линейная интерполяция. По результатам математического моделирования строили распределение температуры шлаковой ванны в каждом опыте и в центре плана эксперимента. Наибольший интерес с точки зрения качества наплавленного слоя представляет анализ температур в хвостовой области шлаковой ванны, пройденной электродом. Пример построения температурного поля по продольному сечению шлаковой ванны показан на рис. 3. Характер распределений температуры является общим для всех построений: расширение области нагрева сразу за электродом с её последующим сужением и поднятием к поверхности ванны, вследствие охлаждения.
Таблица 1
План полнофакторного эксперимента параметров ЭШН
|
№ опыта |
Параметры режима наплавки |
Усреднённые значения полученных данных опыта |
|||||||
|
Нм, мм |
Dэ, мм |
Rб, Ом |
Iн, А |
Vmax,м/с |
fп, Н/м3 |
fk, Н/м3 |
Т0С ТН 20 |
t, с |
|
|
1 |
8 |
35 |
0,09 |
610 |
0,40 |
422 |
647 |
1470 |
0,72 |
|
2 |
14 |
35 |
0,09 |
515 |
0,67 |
318 |
691 |
1360 |
0,62 |
|
3 |
14 |
35 |
0,14 |
465 |
0,60 |
247 |
685 |
1330 |
0,60 |
|
4 |
8 |
35 |
0,14 |
540 |
0,30 |
338 |
756 |
1390 |
0,65 |
|
5 |
15 |
25 |
0,14 |
370 |
0,38 |
416 |
1296 |
1340 |
0,62 |
|
6 |
8 |
25 |
0,14 |
300 |
0,56 |
278 |
904 |
1280 |
0,52 |
|
7 |
14 |
25 |
0,09 |
380 |
0,35 |
459 |
929 |
1230 |
0,46 |
|
8 |
8 |
25 |
0,09 |
330 |
0,77 |
317 |
1347 |
1190 |
0,40 |
|
Нм – межэлектродный промежуток, мм; Dэ – диаметр электрода, мм; Rб – сопротивление балластных реостатов, Ом; Iн – ток наплавки ЭШН, А; vmax – скорость движения твёрдых частиц в шлаковой ванне, м/с; fп – пондеромоторные силы движения расплава, Н/м3; fk – конвективные силы движения расплава, Н/м3; Т0С – температура нагрева твёрдых частиц; t – время движения (пребывания) твёрдой частицы в шлаковой ванне, с |
|||||||||
Для определения характера и численных значений скоростей движения расплава шлака и твёрдых частиц, вносимых в шлаковую ванну, широкое распространение получила киносъёмка [3, 21, 22]. Ввиду труднодоступности исследуемых зон, высокой температуры и агрессивности шлака, применение других средств измерения скоростей движения твёрдых частиц в жидкой шлаковой ванне затруднительно. В настоящей работе киносъёмка проводилась в видимых лучах при установившемся процессе ЭШН кинокамерой «Красногорск-2» со скоростью 24 кадра в секунду через нейтральный фильтр (рис. 4). Для визуализации движения твёрдых частиц в расплаве шлаковой ванны во время киносъёмки на определённую поверхность шлаковой ванны подавали частицы твёрдого сплава различной фракции 0,60-2,8 мм. На кинограмме (рис. 4) движения расплава шлака на свободной поверхности шлаковой ванны видно, что электрод в области сухого вылета нагрет меньше, чем шлак, и хорошо контрастирует с ним. Таким образом, определение места вхождения электрода в шлак не представляет трудностей. В течение всего времени движения по линии АА твёрдые частицы ТН 20 остаются достаточно холодными и на изображении фиксируются в виде темных точек на яркой поверхности шлаковой ванны. В каждом опыте киносъёмку движения твёрдых частиц производили восемь раз. При обработке результатов эксперимента расстояние от электрода до кристаллизатора по линии АА разбивали на три равных участка со скоростями соответственно v1, v2, v3. Замер скоростей производили на монтажном столике с учётом масштаба изображения по величине перемещения твёрдых частиц от кадра к кадру. Интервал времени между кадрами известен и составляет 1/24 с.
После проведения эксперимента с помощью полнофакторного эксперимента построены регрессионные уравнения, связывающие средние скорости v1, v2, v3 с параметрами ЭШН получения КМ (6) [3, 18, 20]:
v1 = 0,15 + 0,008 D`э – 0,006 D`э.Н`м.э – 0,009 D`э.R`б;
v2 = 0,164 – 0,009 D`э.H`м.э – 0,007 D`э.R`б;
v3 = 0,115 + 0,0073 H`м.э – 0,004 D`э .H`м.э – 0,004 D`э.R`б. (6)
где D`э = (Dэ – 30)/5; Н`м.э = (Н м.э – 11)/3; R`б = (Rб – 0,115)/0,025.
В табл. 2 даётся анализ качества моделирования скорости движения твёрдых частиц в расплаве шлака. Наблюдается систематическая абсолютная ошибка моделирования скорости, которая в направлении от электрода в начале отрицательна, затем меняет знак и продолжает расти. В качестве возможных причин этого явления можно указать раздельный аддитивный характер учёта в модели конвективных и электромагнитных сил, а поскольку модель построена для квазистационарных условий, не учитывающих зависимость жидкотекучести шлака от температуры, что, естественно, улавливают натурные измерения.
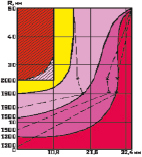
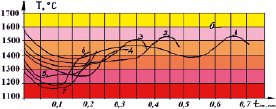
Рис. 3. Температурное поле шлаковой ванны (поперечное и продольное), рассчитанное методом моделирования (сплошные линии) и замеренное термопарами (пунктирные линии)
Для контроля проведено измерение скорости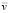 
движения потока шлака механическим устройством (графитовой вертушкой на оси), как на свободной поверхности, так и во внутренних объёмах шлаковой ванны с помощью киносъёмки через кварцевое стекло. Плавное изменение тока наплавки Iн и межэлектродного промежутка Нм.э на 20-30 % слабо сказывается на скорости движения твёрдых частиц и расплава шлака, меняющихся при этом на 10-15 %. Это обуславливает близость результатов измерения скорости движения частиц механическим устройством (вертушкой) и киносъёмкой, полученных для несколько отличных условий [1, 19, 22].
Как показывают результаты исследований в широком рабочем диапазоне изменения параметров ЭШН КМ неплавящимся электродом, направление движения потока расплава жидкого шлака и траектория движения твёрдых частиц на свободной поверхности шлаковой ванны всегда постоянно: от электрода к кристаллизатору. Это способствует траектории движения твёрдых частиц по сравнительно низкотемпературным участкам жидкого шлака, в которых твёрдые частицы нагреваются не выше температуры шлака 1150...1250 °С и, попадая в расплав сплава-связки, хорошо им смачиваются. Такой температурный режим предохраняет твёрдые частицы от чрезмерного разогрева, а следовательно, исключает интенсивное растворение ТН 20 в жидкой матрице КМ [26–28].
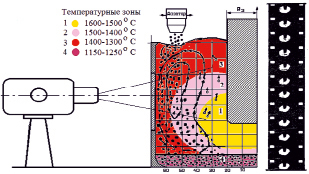
Рис. 4. Скоростная киносъёмка движения твёрдых частиц в шлаковой ванне
Таблица 2
Ошибки моделирования движения твёрдых частиц в шлаковой ванне
|
Опыт |
Скорости движения расплава, м/с |
||||||||
|
v1 |
v2 |
v3 |
|||||||
|
Измеренная |
Моделированная |
Абсол. ошибка |
Измеренная |
Моделированная |
Абсол. ошибка |
Измеренная |
Моделированная |
Абсол. ошибка |
|
|
1. а |
0,173 |
0,150 |
–0,023 |
0,180 |
0,200 |
+0,020 |
0,126 |
0,170 |
+0,044 |
|
2. б |
0,161 |
0,140 |
–0,021 |
0,162 |
0,200 |
+0,038 |
0,122, |
0,160 |
+0,038 |
|
3. в |
0,143 |
0,110 |
–0,033 |
0,148 |
0,180 |
+0,032 |
0,130 |
0,160 |
+0,030 |
|
4. г |
0,155 |
0,11 |
–0,044 |
0,166 |
0,200 |
+0,034 |
0,128 |
0,160 |
+0,032 |
|
5. д |
0,157 |
0,120 |
–0,037 |
0,180 |
0,200 |
+0,020 |
0,130 |
0,160 |
+0,030 |
|
6. е |
0,145 |
0,110 |
–0,035 |
0,162 |
0,180 |
+0,018 |
0,143 |
0,160 |
+0,017 |
|
7. ж |
0,139 |
0,120 |
–0,019 |
0,166 |
0,180 |
+0,014 |
0,122 |
0,140 |
+0,018 |
|
8. з |
0,127 |
0,140 |
0,013 |
0,148 |
0,160 |
+0,012 |
0,144 |
0,146 |
+0,002 |
|
Средняя абсолютная ошибка – 0,027 |
Средняя абсолютная ошибка + 0,023 |
Средняя абсолютная ошибка + 0,026 |
|||||||
В большинстве опытов максимальной являлась скорость v1∈{0,140; 0,195} м/с. Несколько меньше скорость v2∈{0,120; 0,176} м/с. Скорость v3∈{0,99; 0,138} м/с была минимальна. Свободный член максимален в уравнении для v2 и минимален в уравнении для v3. Совместное влияние межэлектродного промежутка Нм и диаметра электрода Dэ на все три скорости отрицательное и наибольшее для v2. Совместное влияние диаметра электрода Dэ и сопротивления балластных реостатов Rб на все скорости также отрицательное. На скорость v2 параметры режима наплавки существенного самостоятельного влияния не оказывают. В то же время возле электрода скорость движения v1 значительно растёт с ростом его диаметра, а v3 ближе к кристаллизатору существенно увеличивается с повышением межэлектродного промежутка. С использованием уравнений (2) и (6) на основе моделирования построены графики, представленные на рис. 5.
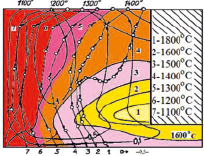
Рис. 5. Зависимость нагрева и скорости движения расплава шлака от параметров ЭШН
Направление движения расплава шлака по свободной поверхности шлаковой ванны является отражением направления движения жидкости в объёме ванны. Хорошо прогретые восходящие потоки проходят вдоль свободной поверхности ванны, препятствуя образованию на ней корки закристаллизовавшегося шлака. Попадая на поверхность шлаковой ванны, твёрдые частицы покрываются шлаковым гарнисажем и становятся своеобразными макрохолодильниками, что предотвращает их интенсивный перегрев и растворимость.
Для горизонтальной ЭШН по слою шихты получена статистическая зависимость средней температуры Тср °С в зоне сплавления КМ с основным металлом в зависимости от функций параметров ЭШН (7) [3, 18, 20]:
Тср = 604,5 – 5750.Rб + 434,37.Vн + 81,25.Fэ – 46,875.Vн.Fэ , (7)
где Rб – сопротивление балластных реостатов (Ом) для регулирования тока наплавки, А; Vн – скорость наплавки, м/ч; Fэ – поперечное сечение электрода, см2.
Приведённые модельные описания движения расплава шлака под действием конвективных тепловых и электромагнитных сил дали возможность проследить поведение в шлаковой ванне твёрдых частиц, вводимых через шлаковую ванну. Дифференциальное уравнение движения твёрдой частицы в виде шара в вязкой жидкости имеет вид [3, 23, 24]:
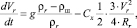(8)
где Vr = υ / Rr – скорость опускания твёрдой частицы в виде шара, м/с (υ – кинематическая вязкость шлака); Rr – радиус твёрдой частицы, м; t – время пребывания твёрдой частицы в расплаве шлака, с; ρr – плотность материала твёрдой частицы, кг/м3; ρшл – плотность расплава шлака, кг/м3; Сх – безразмерный коэффициент гидродинамического сопротивления.
По выполненным исследованиям определяли распределение температуры наплавленного слоя. На установке ИМАШ-9-66 были воспроизведены температурные режимы ЭШН с последующей выдержкой в течение 10 мин и замерены микротвердость как твёрдых частиц Нμ.к, так и матрицы Нμ.м КМ, при заданных температурах. Относительная износостойкость εотн, КМ ТН 20 + колмоной была рассчитана по известной зависимости [3, 23, 24]:
εотн =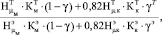 
(9)
где HTμ.м, HЭμ м – микротвердость матрицы, МПа; HТμ.к, НЭμ к – микротвердость карбидов (спечённые твёрдые частицы ТН 20), МПА; КТм, КЭм, КТк, КЭк – эмпирический коэффициент соответственно матрицы и спечённой твёрдой частицы на основе карбидов титана; g – доля твёрдых частиц в КМ; индекс Т – измерения при заданных температурах; индекс Э – измерения для сплава, выбранного за эталон.
Большое влияние на качество наплавленного слоя оказывает главным образом пребывание твёрдых частиц в области высоких температур шлаковой ванны. Для сравнения на установке ИМАШ-9-66 физически моделировались температурные режимы того же КМ без предварительного прохождения твёрдых частиц через слой жидкого расплава шлака, температура которого в некоторых точках (близлежащих к электроду) достигает 1750 °С. Температурные режимы, моделируемые на ИМАШ-9-66, представляют собой быстрый нагрев и выдержку за 10 мин до температуры точки попадания твёрдой частицы в зону наплавки, отстающую от оси симметрии на величину rc. По замеренной микротвердости матрицы и твёрдых частиц для КМ и эталона – сплав сормайт (У30Х28Н4С4) при различных температурах, по формуле (9) была рассчитана температурная зависимость износостойкости εотн, которая составила для 20°С ε20 = 2,2 и ε500 = 3,16. Таким образом, поскольку составляющие КМ лучше и дольше сохраняют свои первоначальные свойства с повышением температуры, а эталон (сплав сормайт) начинает активно разупрочняться с повышением температуры испытания, относительная износостойкость КМ с повышением температуры возросла почти в 1,5–2,5 раза (рис. 6).
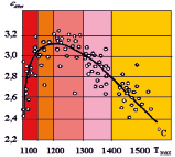
Рис. 6. Зависимость относительной износостойкости εотн КМ от максимальной температуры наплавленного слоя
Наиболее благоприятное влияние на свойства КМ оказывает подача твёрдых частиц в наименее перегретую область шлаковой ванны. При радиусе дозирования rд = 20 мм снижение относительной износостойкости превышает 3 %. По мере удаления точки дозирования от поверхности электрода степень влияния шлаковой ванны на свойства твёрдых частиц постепенно ослабевает и резко падает у поверхности кристаллизатора. Однако при подаче твёрдых частиц в холодную часть шлаковой ванны возникает опасность образования шлакового гарнисажа вокруг частиц твёрдого сплава, который не успевает расплавиться при попадании твёрдых частиц в расплав матрицы, что приводит к образованию шлаковых включений в КМ. В этом случае возможно несплавление твёрдых частиц с матрицей, а следовательно, при абразивном износе такие частицы будут быстро выкрашиваться, что снижает износостойкость наплавленного КМ.
Проведённые исследования показали, что разработанные КМ имеют объёмную долю твёрдых частиц в матрице выше критических величин (примерно 54–57 %), что привело к минимальному образованию сложнолегированных структур и выделению нежелательных фаз на поверхности раздела [2, 26–28]. Рентгеноструктурным анализом установлено, что наиболее распространённой фазой в матрице КМ ТН 20 + колмоной является борокарбид хрома и железа типа М7(СВ)3, которые наблюдаются в виде светлых зёрен округлой формы длиной до 0,56 мм. [2, 24, 25].
Выводы
1. Моделирование температурного поля шлаковой ванны позволило установить, что оптимальным температурам наплавки КМ Топт = 1150–1350 °С соответствуют режимы ЭШН: Iн = 350–420 А; Uшв = 32–38 В; Vн = 0,8–I,2 м/ч; Hмэ = 12–14 мм; Дэ = 35–40 мм; Вшв = 65–100 мм.
2. Составленное регрессионное уравнение полнофакторного эксперимента зависимости температуры наплавленного КМ от параметров режима ЭШН позволило определить оптимальные области подачи частиц твёрдого сплава в расплав матрицы, с целью предотвращения растворения твёрдых частиц в матрице.
3. Применение разработанных устройств для математического моделирования температурного поля шлаковой ванны, посредством определения удельной электропроводности расплава жидкого шлака, позволило снизить вмешательство в нормальный ход технологических процессов, повысить точность измерений, а следовательно, повысить высокотемпературную износостойкость КМ.
4. Найденные закономерности изменения скорости движения расплава на свободной поверхности шлаковой ванны в зависимости от параметров режима ЭШН можно использовать как для отработки технологии наплавки, так и при создании моделей шлаковых ванн.
Библиографическая ссылка
Быстров В.А. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНОГО ПОЛЯ ШЛАКОВОЙ ВАННЫ ЭШН КОМПОЗИЦИОННЫХ СПЛАВОВ // Современные наукоемкие технологии. – 2020. – № 6-1. – С. 15-24;URL: https://top-technologies.ru/ru/article/view?id=38065 (дата обращения: 19.04.2024).