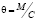Обширный класс современных строительных конструкций имеет своей основой тонкостенные стержневые профили, соединенные между собой. В этих профилях возникает сложное напряженное состояние, частью которого является кручение. Задача о кручении стержня углового прокатного профиля является частным случаем задачи Ламе, в которой в вершине входящего угла теоретические значения напряжений стремятся к бесконечности [1]. Решение задач с такими сингулярностями является сложной математической проблемой. Результаты исследований напряжений, возникающих при деформировании прокатных профилей, являются темой большого числа научных публикаций.
Обзор литературы по исследованию стыковых соединений тонкостенных стержней и оболочек выполнен в [2]. Рассмотрены различные теоретические, численные и экспериментальные подходы к моделированию, анализу и проектированию тонкостенных структур, соединенных вдоль их общих границ. Рассмотрено несколько альтернативных форм граничных условий, условий непрерывности и скачков на сингулярных срединных кривых, моделирующих соединение.
В [3] выполнено конечно-элементное и экспериментальное моделирование нового типа многоплоскостного соединения для изменения уклона в длинно-пролетной передающей башне линии высоковольтной электропередачи. Помимо изгибающих моментов, в элементах системы наблюдались крутящие моменты и соответствующие напряжения.
В [4] решалась теоретическая задача Дирихле для уравнения Пуассона для стержня квадратного поперечного сечения с применением серендиповых конечных элементов. Доказано, что в задаче расчета кручения стержня квадратного сечения методом конечных элементов (МКЭ) новые альтернативные модели биквадратичного конечного элемента позволяют получить большую точность в сравнении с известным стандартным элементом.
Вопрос о введении нового конечного элемента для расчета кручения стержня открытого профиля рассмотрен в [5]. Выполнено сравнение аналитического и численного решений для стержня двутаврового сечения без учета и с учетом деформаций сдвига с использованием двух видов аппроксимации для функций формы.
Таким образом, тема исследования напряженного состояния тонкостенных угловых профилей является актуальной, содержащей множество неизученных теоретически и практически важных вопросов. В связи с этим есть проблема выбора адекватного инструмента численного анализа возникающих краевых задач. Коммерческие программы часто недоступны по цене для исследователя, в то время как свободно распространяемые продукты могут быть сопоставимы с ними по качеству результатов.
Одним из таких пакетов является FreeFEM++ [6]. Он применялся в [7] к исследованию задачи об установившейся вибрации предварительно напряженной пластины на основе модели Кирхгофа. Дана оценка точности решения прямой задачи для узкой однородной пластины методом конечных элементов путем сравнения с аналитическим решением. Анализ продемонстрировал высокую точность решения МКЭ, и сделан вывод о том, что пакет FreeFEM++ предоставил адекватные численные результаты для рассмотренной пластины.
Целью данной статьи является исследование возможности применения пакета FreeFEM++ к анализу напряженно-деформированного состояния при кручении стержня углового профиля, и разработка алгоритма этого анализа. Основным методом исследования является сравнение численного решения задачи МКЭ с известным из литературы решением.
Поставлены задачи:
1. Создания алгоритма нахождения и визуализации решения МКЭ в пакете FreeFEM++.
2. Сравнения результатов расчетов кручения стержня:
а) круглого сечения;
б) углового сечения с толстыми стенками;
в) тонкостенного углового сечения.
Рассматривается упругий стержень с поперечным сечением, представленным на рис. 1. Ставится задача о свободном кручении этого стержня двумя равными по модулю и противоположными по направлению крутящими моментами, приложенными к его концам. Краевая задача будет решаться в области Ω с границей L0, рис. 1.
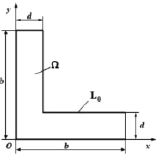
Рис. 1. Геометрия поперечного сечения
Известно [8], что выбором вида решения задача о кручении стержня сводится к краевой задаче для уравнения Пуассона:
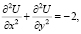(1)
где U(x, y) – функция напряжений Прандтля. Для односвязных стержней:
U = 0 на границе области L0. (2)
Касательные напряжения находим как
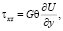
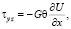
где G – сдвиговый модуль Юнга.
Угол закручивания на единицу длины стержня θ определяем из выражения для крутящего момента [8]:
M = Cθ,
где C – крутильная жесткость стержня, для сплошных стержней определяется как [9]
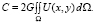
Итак, будем решать краевую задачу Дирихле для уравнения Пуассона (1), (2).
Материалы и методы исследования
С помощью пакета FreeFEM++, который позволяет строить численное решение двумерных краевых задач методом конечных элементов, решены задачи о кручении стержня круглого и углового поперечного сечения.
Алгоритм решения задачи во FreeFEM++:
1. Запишем задачу (1), (2) в вариационной постановке
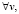
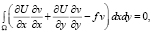
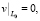(3)
где f = 2.
2. Зададим на языке FreeFEM++ поперечное сечение стержня – область в параметрическом виде, в которой решается задача.
3. Произведем триангуляцию области при помощи встроенного генератора сеток, основанного на алгоритме Делоне – Вороного.
4. Приближенное решение задачи (3) ищем в виде
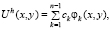(4)
где φk(x, y) – базисные функции, в качестве которых выбраны кусочно-линейные непрерывные конечные элементы (барицентрические координаты), ck – коэффициенты, подлежащие определению. Таким образом, формула (4) задает аппроксимацию функции U(x, y) в виде некоторого сужения на конечномерное пространство, определяемое базисом φk(x, y), k = 1..n – 1.
5. Запишем на языке FreeFEM++ вариационную формулировку задачи с краевыми условиями и зададим способ решения СЛАУ (по умолчанию несимметричный мультифронтальный метод решения разряженных систем линейных уравнений).
6. Определим крутильную жесткость стержня C и угол закручивания на единицу длины θ средствами языка FreeFEM++.
7. Найдем касательные напряжения τxz и τyz и выполним их визуализацию. Средства пакета FreeFEM++ позволяют сохранять построенные изображения в postscript файл при помощи команды plot c параметром ps.
Численный эксперимент проведен со следующими параметрами: G = 80 ГПа, M = 10 кН·м, для задачи А) о кручении стержня круглого поперечного сечения R = 40 мм; для задачи Б) о кручении стержня углового профиля b = 80 мм, d = 38 мм; для задачи В) о кручении стержня углового профиля b = 80 мм, d = 8 мм.
Результаты исследования и их обсуждение
Задача А. В результате вычислений по представленной выше методике сформированы изображения распределений значений касательных напряжений в круговом стержне, представленные на рис. 2.
Максимальные и минимальные значения касательных напряжений приведены в табл. 1.
Таблица 1
Предельные значения касательных напряжений в стержне круглого сечения
|
Напряжения |
Max |
Min |
|
τxz |
110 МПа |
–110 МПа |
|
τyz |
110 МПа |
–110 МПа |
Найдены значения крутильной жесткости стержня C = 321 699 Н·м2 и угла закручивания на единицу длины θ = 0,031.
а)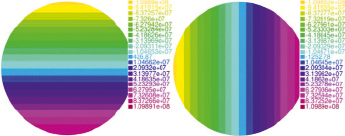
б)
Рис. 2. Касательные напряжения в стержне круглого профиля: а) τxz, Па; б) τyz, Па
Сравнение полученных результатов проведено с источником [9, с. 92], где крутильную жесткость можно определить по формуле
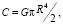
из которой получено значение 321 699 Н·м2, что согласуется с численным результатом.
Для задач Б и В результат распределения значений касательных напряжений в стержне углового профиля, представлен на рис. 3 и 4.
Максимальные и минимальные значения касательных напряжений для обеих задач сведены в табл. 2.
Жесткость при кручении прокатных профилей приближенно можно вычислить по формуле [8, с. 266]:
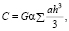(5)
где a и h – высота и толщина отдельных прямоугольников. Коэффициент α учитывает влияние соединения отдельных прямоугольников для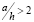 
. Экспериментальные значения коэффициента α [8, с. 266] и рассчитанные для него крутильная жесткость и угол закручивания, а также результаты расчета во FreeFEM++ приведены в табл. 3.
Из табл. 3 видно, что значения крутильной жесткости и угла закручивания, полученные при помощи пакета FreeFEM++, находятся в допустимом диапазоне значений.
Заключение
Создан алгоритм численного анализа и визуализации его результатов для решения задачи о свободном кручении стержня углового прокатного профиля методом конечных элементов в пакете прикладных программ FreeFEM++. Полученные численные результаты хорошо согласуются с известными решениями задач о кручении стержней круглого, углового и тонкостенного углового профилей.
а)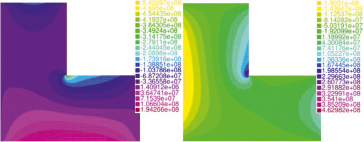 
б)
Рис. 3. Касательные напряжения в стержне углового профиля задача Б: а) τxz, Па; б) τyz, Па
а)
б)
Рис. 4. Касательные напряжения в стержне углового профиля задача В: а) τxz, Па; б) τyz, Па
Таблица 2
Предельные значения касательных напряжений в стержне углового сечения
|
Напряжения |
Max |
Min |
||
|
Задача Б |
Задача В |
Задача Б |
Задача В |
|
|
τxz |
194 МПа |
4 049 МПа |
– 542 МПа |
– 11 414 МПа |
|
τyz |
463 МПа |
15 915 МПа |
– 190 МПа |
– 4 274 МПа |
Таблица 3
Проверочные и расчетные значения крутильной жесткости и угла закручивания для задач Б и В
|
Коэффициент α для углового профиля |
Крутильная жесткость С, рассчитанная по формуле (5), Н·м2 |
Угол закручивания |
||||
|
Задача Б |
Задача В |
Задача Б |
Задача В |
|||
|
По опытам А. Феппля |
Для различных образцов |
0,86–1,10 |
153 524–196 368 |
1 784–2 282 |
0,051–0,065 |
4,380–5,602 |
|
Средний |
0,99 |
176 731 |
2 054 |
0,056 |
4,867 |
|
|
По опытам ЦНИИПСа |
1,0 |
178 516 |
2 075 |
0,056 |
4,819 |
|
|
Расчет во FreeFEM |
154 813 |
2 030 |
0,064 |
4.925 |
||
Установлено, что численные значения касательных напряжений и углов закручивания в рассмотренной задаче при расчете тонкостенного углового профиля существенно превышают их предельно допустимые значения, обычно принимаемые при расчетах на прочность и жесткость. Этот результат получен как при использовании стандартного инженерного метода, так и при решении в пакете FreeFEM++.
В целом пакет прикладных программ FreeFEM++ является надежным инструментом решения стандартных технических задач анализа кручения стержней методом конечных элементов, с возможностями наглядного представления результатов расчета.
Численные эксперименты были проведены на вычислительном кластере ЦКП «Центр данных ДВО РАН».
Библиографическая ссылка
Рябоконь А.С., Ткаченко О.П. АЛГОРИТМ ЧИСЛЕННОГО АНАЛИЗА КРУЧЕНИЯ СТЕРЖНЕЙ ПРОКАТНОГО ПРОФИЛЯ В ПАКЕТЕ ПРИКЛАДНЫХ ПРОГРАММ FREEFEM++ // Современные наукоемкие технологии. – 2020. – № 5. – С. 96-100;URL: https://top-technologies.ru/ru/article/view?id=38038 (дата обращения: 03.12.2024).