Формирование достоверных физико-геологических моделей сред изучаемых регионов является основой для выявления перспективных зон нефтегазоносности, что, в свою очередь, позволяет эффективно принимать решения о проведении поисковых геологоразведочных работ. Наличие согласованной с геофизическими полями модели строения осадочного чехла является важнейшим условием успешной геологической интерпретации. Построение необходимых для этого структурно-плотностных моделей исследуемой среды, с заданной степенью удовлетворяющей наблюденному гравитационному полю и соответствующих имеющимся представлениям о строении изучаемой площади, осуществляется решением обратных задач гравиразведки. В этой связи является важным выбор метода и параметров решения для получения наилучшего результата.
Цель исследования: определение оптимальных параметров решения обратной задачи гравиразведки в рамках критериального подхода с интегральным критерием оптимальности и итерационным методом решения.
Материалы и методы исследования
Процесс моделирования включает в себя решение обратных задач гравиразведки в двух постановках (поиск конфигурации структурного фактора и изучение аномального дифференцирования плотностных характеристик) [1–3]. Одним из наиболее эффективных подходов к решению обратной задачи является критериальный. В его основе лежит нахождение оптимального относительно заданного критерия оптимальности J [σ, g] или J [f, g] решения обратной задачи. В качестве нулевого приближения рассматривается модель g, а функционал J содержит дополнительную информацию о неоднородности данных или положении плотностных границ, на основе которых выполнялись построения [4; 5, с. 188–195]. Критерий обеспечивает доопределение решаемой задачи реконструкции изучаемого параметра, в нашем случае это или плотностные характеристики, или глубины залегания границ.
Плотностная задача гравиразведки
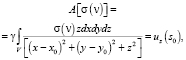
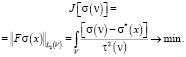(1)
Для ее решения требуется найти такое распределение плотности σ(ν) по наблюдаемой uz(s0), которая минимизирует J[σ(ν)] и удовлетворяет наблюдаемой uz(s0) = uz(x0, y0) с заданной степенью точности e. Требуемая точность задается исходя из свойств исходных данных и цели последующего использования модели. Здесь n – область нижнего полупространства (может быть и двумерная n = s = (x, z), и трехмерная n = (x, y, z)), где необходимо найти распределение параметра, s0 – область наблюдения поля uz, g – гравитационная постоянная. Параметр τ2(ν), входящий в конструкцию критерия оптимальности (1), можно интерпретировать как величину, связанную с априорной оценкой достоверности (среднеквадратичной погрешности построения) нулевого приближения σ*(ν). В (1) имеются также F – линейный замкнутый оператор, F* – сопряженный к F оператор.
Итерационный алгоритм построения сходящейся последовательности искомого параметра основан на принципе наискорейшего убывания невязки по полю, реализует вариационный принцип равномерной оптимизации заданной модели [6]. Для линейных задач, каковой является плотностная, вычислительная схема итерационного алгоритма последовательных приближений реализуется в форме
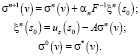(2)
Здесь αn – параметр релаксации, выбираемый по требованию скорейшего убывания невязки, при этом скорость убывания невязки обеспечивается следующим его значением:
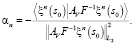(3)
Алгоритм (2, 3) монотонно сходится к решению уравнения (1). Критерием его остановки служит достижение требуемого уровня невязки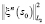 
.
Параметр, регулирующий свойства оптимальности, это оператор F-1 – обратный к F оператор. Он выражает априорные данные о строении изучаемой среды на момент очередного шага решения обратной задачи и может уточняться в процессе вычислений.
Следует помнить, что полученное решение является оптимальным лишь с точки зрения задаваемой модели и критерия. На самом деле мы получаем одно из допустимых, априори равноправных решений при других условиях. В зависимости от целей модель можно упростить или наполнить дополнительными данными и рассматривать решение в этих классах моделей. Выбор параметрической размерности (сложности) модели возмущающих объектов, согласованный с объемом априорной информации, является фактором, во многом предопределяющим качество решений обратных задач [7, 8].
Если решение плотностной задачи не дает удовлетворительных результатов, требуется уточнить расположение структурно-плотностных границ путем решения структурной задачи.
В структурной модели среды задаются плотности в N пластах и N + 1 границ zi = fi(x, y), характеризующих глубину залегания z в зависимости от координат s = (x, y) на поверхности, для двухмерного случая s = x. Координаты точек наблюдения s0 = (x0, z0). Вертикальное изменение плотности в структурной модели не допускается. Связь между структурными элементами –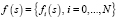 
, 
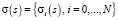и «наблюдаемой» вертикальной производной гравитационного потенциала uz(s0) в области S нижнего полупространства (z > 0) имеет вид
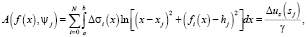
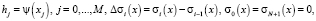(4)
где [a, b] – профиль, вне которого границы выходят на асимптоты и их влияние (боковых зон) учитывается отдельным образом,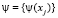 
– высоты рельефа, в точках которого 
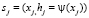задано поле, М + 1 – количество точек наблюдения, 
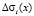– перепад плотности на контакте с номером i. Соотношение (4) в операторном виде вместе с критерием:
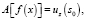
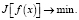(5)
Можно считать, что для каждой точки профиля возможные глубины залегания границ образуют множество, где для каждых двух произвольно взятых глубин одной границы, z1 и z2, можно указать, какая из них наиболее предпочтительна, или они имеют одинаковый ранг (приоритет), в том числе ранг недопустимой глубины (например, на дневной поверхности или выше нее). Алгоритм (5) решения (1) строится аналогично случаю плотностной задачи.
Проведем ряд экспериментов, позволяющих определить наилучшие параметры решения обратной плотностной задачи гравиразведки для получения оптимального результата при минимальной затрате времени для выбранного критерия и алгоритма (1–3). Решение будем проводить в программном редакторе геолого-геофизических моделей среды GeoVIP [4, 9].
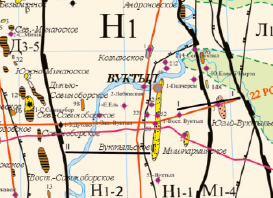
Для исследований были выбраны два профиля, расположенные в различных структурно-тектонических зонах (рис. 1). Профиль I–I расположен в пределах восточного борта Верхнепечорской впадины и Среднепечорского поперечного поднятия, профиль II–II пересекает Печоро-Илычскую моноклиналь Верхнепечорской впадины, где по данным сейсморазведки выделяются рифогенные постройки. Рассматриваемая территория покрыта детальными гравиметрическими съемками масштаба 1:25 000 и 1:50 000. Анализ гравиметрических карт в пределах впадины показал, что среднеквадратическая ошибка определения аномалий Буге в пределах Верхнепечорской впадины составляет ±0,2–0,25 мГал. Учитывая погрешность съемок, можно полагать, что по их данным принципиально возможно выявление объекта, если гравитационный эффект от него превышает величину 0,2 мГал. Такой эффект на картах масштаба 1:25 000 и 1:50 000 будет проявляться в виде малоамплитудных аномалий, в основном в изгибах изоаномал. В последнее время исследователи ТПП особое внимание уделяют выделению органогенных построек как элементов, связанных с перспективами запасов нефти и газа. В нашем случае выделение на картах гравитационного поля и его трансформант рифов доманико-турнейского возраста, расположенных на глубинах 2500–3000 м, довольно проблематично. Тем не менее геоплотностное моделирование, основанное на решении обратных задач гравиразведки, в комплексе с данными сейсморазведки, позволяет выделить плотностные характеристики, связанные с литологическими неоднородностями осадконакопления.
Результаты исследования и их обсуждение
Рассмотрим профиль I–I. Длина профиля 40000 м, глубина 13000 м. Для получения полезной информации об изучаемой территории длина профиля к его глубине должна относиться не менее чем 3:1. Для определения интересующих нас параметров имеются установленные погрешности [10] (табл. 1).
Для определения критериев оптимальности при решении обратных задач гравиразведки необходимо, чтобы искомое решение минимально отклонялось от заданного нулевого приближения с учетом различной степени достоверности его построения в задаваемых точках. Значения весового множителя задаются в пределах от 0 до 1.
|
|
Н1 – Верхнепечорская впадина Н1-1 – Вуктыльская тектоническая пластина Н1-2 – Печоро-Илычская моноклиналь М1 – Среднепечорское поперечное поднятие М1-4 – Югид-Кыртинская антиклинальная зона –– профили I–I и II–II |
Рис. 1. Схема расположения профилей
Таблица 1
Интервалы варьирования параметров и погрешностей гравиметрической съемки
|
Параметр |
Значение |
|
Масштаб отчетной карты |
1:25 000 |
|
Сечение изоаномал, мГал |
0,25 |
|
Средняя квадратическая погрешность определения аномалии Буге, мГал |
±0,1 |
|
Средняя квадратическая погрешность определения наблюденных значений силы тяжести, мГал |
±0,06 |
|
Полная погрешность интерполяции, мГал |
±0,2 |
|
Средняя квадратическая погрешность определения высот, м |
±0,350 |
|
Средняя квадратическая погрешность определения координат пунктов относительно Государственной геодезической сети, м |
±20 |
|
Число пунктов на 1 км2 |
12–16 |
|
Расстояния между пунктами при наблюдениях по профилям, м |
50–250 |
Исследования проводились с учетом следующих начальных параметров:
Максимальная глубина исследований – hmax = 13 000 м = 13 км;
Глубина залегания рассматриваемой плотностной неоднородности – h (км);
Вспомогательный коэффициент b = 1/hmax = 1/13;
Значение критерия – k = b h = (1/13) h.
Интегральные критерии оптимальности и, в частности, имеющие вид квадратичной формы, отражают усредненные характеристики искомого решения. В случае имеющихся сведений о высокой степени достоверности информации, используемой при начальном построении, таких как данные бурения, ГИС, лабораторных исследований, критерий оптимальности можно уменьшить, а если имеется недостаток данных, то значение его необходимо увеличить. В частности, в пределах территории, достаточно разбуренной поисковыми скважинами, параметр критерия оптимальности берется близким к 0, а по мере удаления от таких мест – к 1. Исходя из этих соображений, для плотностной задачи критерий был пересмотрен.
Обратная задача решена для профиля I–I (длина L = 40000 м) до пяти итераций (табл. 2) со следующими параметрами:
Δx – шаг интерполяции границ и решения прямой и обратной задач (м);
d – количество интервалов по профилю: d = L/Δx или d = [L/Δx] + 1;
δпр – невязка при решении прямой задачи (мГал);
δобр – невязка при решении обратной задачи (мГал);
T – время решения обратной задачи для пяти итераций и соответствующем шаге (с).
Таблица 2
Зависимость невязки при решении обратной плотностной задачи от Δx для 5 итераций (профиль I–I)
|
L = Δx*d, d∈N |
L ≈ Δx*d, d∈N |
||||||||||||
|
Δx, м |
50 |
80 |
100 |
125 |
160 |
200 |
250 |
320 |
176 |
227 |
285 |
300 |
350 |
|
d |
800 |
500 |
400 |
320 |
250 |
200 |
160 |
125 |
227 |
177 |
140 |
133 |
114 |
|
T, с |
183 |
41 |
29 |
19 |
17 |
8 |
6 |
6 |
11 |
9 |
6 |
6 |
5 |
|
Δz, м |
50 |
100 |
100 |
125 |
150 |
200 |
250 |
300 |
150 |
200 |
250 |
320 |
320 |
|
δпр, мГал |
6,00 |
6,01 |
5,88 |
5,69 |
5,58 |
5,56 |
5,53 |
5,24 |
9,21 |
8,99 |
12,02 |
12,37 |
11,86 |
|
δобр, мГал |
0,26 |
0,26 |
0,28 |
0,31 |
0,33 |
0,36 |
0,38 |
0,48 |
0,55 |
0,57 |
1,01 |
1,07 |
1,08 |
Рис. 2. График зависимости δобр = δобр(Δx) для пяти итераций решения обратной задачи для профиля I–I для шага Δx: L ≈ Δx*d
Шаг интерполяции по глубине Δz выбирается соразмерно шагу Δx. Следует отметить, что шаг интерполяции при решении прямой и обратной задач гравиразведки должен быть одинаков, иначе алгоритм может привести к ухудшению результата, т.е. увеличению значений невязок.
На рис. 2 показан график зависимости невязки при решении обратной задачи от произвольного шага.
По полученным результатам можно утверждать, что алгоритм расчета неустойчив относительно произвольного шага. Поэтому следует выбирать Δx: L = Δx*d, d∈N. В табл. 3 приведена полученная зависимость такого шага и числа итераций. Оптимальным шагом, соответствующим минимальному числу итераций при условии минимизации времени расчета обратной задачи, следует считать 100 м.
Таблица 3
Зависимость количества итераций (It – количество итераций) для достижения удовлетворительной невязки 0,25 мГал при решении обратной плотностной задачи от Δx
|
Δx |
50 |
80 |
100 |
125 |
160 |
200 |
250 |
320 |
|
It |
7 |
7 |
7 |
9 |
9 |
11 |
13 |
17 |
Для невязки 0,125 мГал количество итераций увеличилось в несколько раз. Для теста была решена обратная плотностная задача для шага 80 м и 100 м. Количество итераций для этих шагов увеличилось с 7 (невязка 0,25 мГал) до 25 и 29 соответственно для невязки 0,125 мГал. Анализ результатов экспериментов показал, что оптимальной надо считать невязку 0,25 мГал.
Решение обратной плотностной задачи гравиразведки для начальной модели, построенной по имеющимся данным бурения, сейсморазведки и по заданным плотностным характеристикам комплексов горных пород, для оптимального выбранного значения шага Δx, равного 100 м, количества итераций – 7, выявило невязку между наблюденным и рассчитанным полем до 6 мГал, после решения обратной задачи – порядка 0,24 мГал.
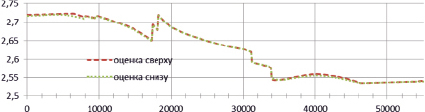
а)
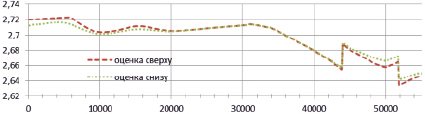
б)
Рис. 4. Варьирование плотностных характеристик по профилю II–II на глубине: а) 3000 м; б) 5000 м
Далее осложним наблюдаемое поле помехой в пределах 10 % имеющихся значений. Для наглядности полученные интервалы изменения плотностных характеристик покажем на срезах 3000 м (рис. 3, а) и 5000 м (рис. 3, б).
Максимальная невязка между верхней и нижней границами плотностей на данных срезах соответственно равна 0,00886 г/см3 и 0,00880 г/см3. Таким образом, результаты показывают, что наличие погрешности поля в 10 % для данной модели практически не влияет на плотностные характеристики. Погрешность зависит и от глубины исследования, но так как в нашем случае значения критерия на указанных глубинах равны с точностью до сотых, то максимальная невязка почти не отличается.
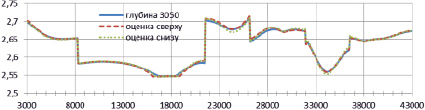
а)
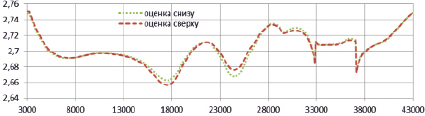
б)
Рис. 3. Варьирование плотностных характеристик по профилю I–I на глубине: а) 3000 м; б) 5000 м
Таблица 4
Зависимость невязки при решении обратной плотностной задачи для профиля II–II от Δx для пяти итераций
|
L = Δx*d, d∈N |
L ≈ Δx*d, d∈N |
||||||||||
|
Δx, м |
50 |
100 |
125 |
200 |
220 |
250 |
275 |
440 |
81 |
174 |
316 |
|
d |
1100 |
550 |
440 |
275 |
250 |
220 |
200 |
125 |
679 |
316 |
174 |
|
T, с |
300 |
45 |
26 |
12 |
11 |
8 |
8 |
5 |
68 |
16 |
8 |
|
Δz, м |
50 |
100 |
125 |
200 |
200 |
250 |
250 |
300 |
100 |
150 |
300 |
|
δпр, мГал |
10,34 |
10,37 |
10,34 |
10,44 |
10,44 |
10,47 |
10,49 |
10,54 |
10,34 |
10,1 |
10,06 |
|
δобр, мГал |
0,46 |
0,45 |
0,45 |
0,45 |
0,45 |
0,43 |
0,44 |
0,79 |
0,52 |
0,98 |
0,85 |
Рассмотрим профиль II–II. Проведем такие же исследования для профиля II–II (длина L = 55000 м) до пяти итераций с критерием, установленным аналогично случая с профилем I–I (табл. 4). Для невязки 0,125 мГал количество итераций увеличилось в несколько раз. В этом случае решение прямой задачи гравиразведки для начальной модели, построенной по имеющимся данным бурения, сейсморазведки и по заданным плотностным характеристикам комплексов горных пород, при значении шага Δx = 125 м, выявило невязку между наблюденным и рассчитанным полем до 10,34 мГал.
Для получения оптимальных значений невязки 0,117 мГал было проведено 16 итераций (табл. 5). После решения обратной задачи с количеством итераций, равным 8, невязка составила 0,22 мГал. Анализ выполненных операций позволил выбрать шаг Δx = 125 м и невязку 0,25 мГал.
Таблица 5
Зависимость количества итераций (It – количество итераций) для достижения удовлетворительной невязки 0,25 мГал при решении обратной плотностной задачи для профиля II–II от Δx
|
Δx |
50 |
100 |
125 |
200 |
220 |
250 |
275 |
440 |
|
It |
8 |
8 |
8 |
9 |
10 |
8 |
10 |
117 |
Далее осложним наблюдаемое поле помехой в пределах 10 % имеющихся значений (рис. 4, а, б). Максимальноая невязка между верхней и нижней границей плотностей на срезах 3000 м и 5000 м составила соответственно 0,007447 г/см3 и 0,008879 г/см3.
Результаты проведенных исследований показывают, что наличие погрешности поля в 10 % практически не влияет на плотностные характеристики. Это подтверждает утверждение о том, что погрешности такого порядка не несут серъезных изменений в построенных моделях.
Следует помнить, что полученное решение является оптимальным лишь с точки зрения задаваемой модели и критерия. Все эксперименты проводились с постоянными первоначально заданными значениями параметров. На эффективность исследований в зависимости от решаемых геологических задач значительно влияет масштаб съемки, степень изученности, наличие информации о геологическом строении. В сложных структурно-тектонических зонах упрощенные модели иногда предпочтительней, чем сложные, относительно выбранного критерия качества решения. В любом случае объем априорной информации напрямую влияет на допустимую сложность задаваемой модели.
Полученные результаты решения обратной плотностной задачи гравиразведки соответствуют необходимой точности, поэтому структурная задача не решалась.
Перейдем к описанию полученных моделей.
Профиль I–I (рис. 5) пересекает разные структурно-тектонические зоны – восточный борт Верхнепечорской впадины и Югид-Кыртинскую зону Снеднепечорского поперечного поднятия. Характер распределения гравитационного поля в пределах изучаемого профиля соответствует тектоническим элементам.
Западная часть профиля характеризуется отрицательными значениями гравитационного поля, которые связаны с большой мощностью теригенных пород и понижением основной гравитирующей границы – кровли карбонатов. Восточная часть – Югид-Кыртинская антиклинальная зона отображается в наблюденном поле максимумами поля силы тяжести. Распределение изолиний плотности осадочного чехола на расчетной модели довольно рельефно. В пределах Верхнепечорской впадины отмечаются зоны повышенной плотности – пикеты 9000–12000 и зоны разуплотнений – пикеты 17000–18000. В западной части профиля на геоплотностном разрезе хорошо выделяется надвиг Югид-Вуктыльской структуры. Значения плотности отложений верхнего девона составляют 2,68–2,72 г/см3, в породах среднего девона – 2,60–2,65 г/см3. Отмечаются области разуплотнений в поднадвиговой части разреза. Породы фундамента характеризуются высокими значениями плотностей, от 2,85 до 2,92 г/см3.
На рис. 6 показан результат решения обратной задачи гравиразведки в классе распределения плотностей по профилю II–II, расположенному в пределах Печоро-Илычской моноклинали от западного ее борта (месторождение Восточный Савинобор) до Вуктыльской складки. Гравитационное поле характеризуется понижением значений с запада на восток и хорошо коррелирует с поведением подошвы терригенных отложений. На геоплотностном разрезе ярко выраженной литолого-физической границей отмечается кровля карбонатного доманиково-нижнепермского комплекса, плотности отложений которого колеблются от 2,65 до 2,71 г/см3.
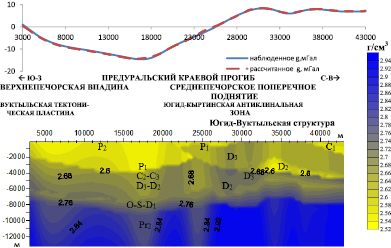
Рис. 5. Геоплотностная модель по профилю I–I. Решение обратной плотностной задачи. Невязка 0,25 мГал и семи итераций
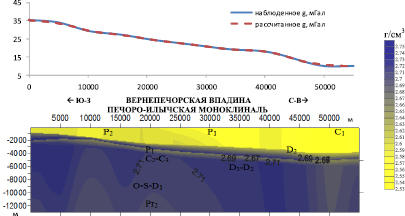
Рис. 6. Геоплотностная модель по профилю II–II. Невязка 0,22 мГал и восьми итераций
Плотности пород верхнего терригенного комплекса варьируют в пределах 2,55–2,60 г/см3, уменьшаясь в восточном направлении. Интересующих нас объектов доманиково-нижнепермского комплекса, в виде плотностных неоднородностей, т.е. зон разуплотнений или объектов с повышенными плотностными свойствами, связанными с рифогенными постройками, не выявлено. Породы, залегающие ниже, характеризуются дифференциацией плотностей от 2,71 до 2,75 г/см3.
Выводы
На качество построенных нулевых приближений моделей сред, в том числе не осложненных резкими перепадами границ и плотностей, в первую очередь влияет качество и количество исходной информации. Это же определяет и сложность модели. Дальнейшая работа состоит в уточнении начальных построений и зависит от выбранного метода решения.
В случае решения обратной плотностной задачи гравиразведки итерационным методом с использованием интегрального критерия оптимальности, в тех областях, где относимся к имеющимся данным с высокой степенью доверия, этот весовой множитель берем близким к 0, а в случае недостатка информации или если она не подтверждена – к 1. Кроме того, в каждом задаваемом слое задаются возможные интервалы изменения плотностей. При выборе этого параметра интерпретатору придется самому оценить данные и в случае необходимости вносить поправки после первых шагов решения обратной задачи и в нулевое приближение к решению, и в значения критерия.
Для случая детальных гравиметрических съемок масштаба 1:25 000 и 1:50 000 при решении выбранным методом двумерных задач при расположения рядовых пунктов съемки 50 м – 250 м, шаг решения обратной задачи и интерполяции следует выбирать в пределах второй четверти интервала интервала 50 м – 250 м, и он должен целое число раз укладываться в длине профиля. В этом случае достигается минимум невязки полей с учетом минимизации времени расчета.
Установлено, что оптимальная невязка наблюденного и рассчитанного полей, где построенная модель соответствует наблюденному полю именно с этой погрешностью, должна соответствовать сечению изоаномал 0,25 мГал. Уменьшение невязки не влияет на достоверность модели, а только ведет к увеличению временного интервала вычислений и количества итераций.
Результаты экспериментов позволяют утверждать, что погрешность (помехи) в значениях наблюденного поля в пределах 10 % не несут серъезных изменений в построениях. Для приведенного примера при интервале плотностей 2,53–2,94 г/см3 максимальная невязка плотностей не превышает 0,007–0,009 г/см3.
Выработанные рекомендации можно использовать для решения обратных задач гравиразведки в рамках критериального подхода с интегральным критерием оптимальности и итерационным методом решения для площадей со схожей структурой.
Библиографическая ссылка
Мотрюк Е.Н., Вельтистова О.М. ВЫБОР ОПТИМАЛЬНЫХ ПАРАМЕТРОВ РЕШЕНИЯ ОБРАТНЫХ ЗАДАЧ ГРАВИРАЗВЕДКИ НА ОСНОВЕ КРИТЕРИАЛЬНОГО ПОДХОДА ДЛЯ ПЛОЩАДЕЙ ТИМАНО-ПЕЧОРСКОЙ ПРОВИНЦИИ // Современные наукоемкие технологии. – 2020. – № 5. – С. 70-78;URL: https://top-technologies.ru/ru/article/view?id=38034 (дата обращения: 21.11.2024).