Одной из основных тенденций развития поршневых двигателей внутреннего сгорания является повышение их мощности и экономичности при обеспечении экологических показателей, принятых на все годы их выпуска и эксплуатации. Анализ статистических данных по выпуску поршневых двигателей зарубежного производства различного назначения показывает, что мощность выпускаемых новых модификаций возрастает в среднем на 60–80 % за каждые 10 лет [1]. При форсировании нового или модернизированного двигателя по среднему эффективному давлению происходит неизбежное повышение температуры в камере сгорания, а значит, и повышение температурных напряжений во всех деталях, которые ее окружают. Как было показано в наших работах [2, 3], при изготовлении ГЦ ее нагружают постоянными силами при запрессовке седел и втулок клапанов. При сборке поршневого двигателя ГЦ дополнительно нагружается при затяжке шпилек крепления ее, при затяжке гайки крепления форсунки. Под действием этих нагрузок определяют напряженно-деформированное состояние (НДС) ГЦ. Однако при работе дизеля значительные напряжения возникают в основном от тепловых нагрузок [4–6], вызванных перепадом температур на огневой поверхности ГЦ. Для оценки работоспособности и надежности ГЦ еще на этапе проектирования на основе расчетных температурных полей определяют тепловое напряженно-деформированное состояние. Это позволяет наиболее эффективно использовать конструкцию ГЦ, а также правильно выбрать материал и систему охлаждения. Таким образом, расчет теплового напряженно-деформированного состояния (ТНДС) является основным в расчете ГЦ. При работе четырехтактного дизеля температура в камере сгорания (КС) меняется в соответствии с рабочим циклом. За счет перепада температур на огневом днище ГЦ возникает перепад температур, что вызывает появление значительных напряжений (по нашим расчета температурные напряжения больше чем в три раза превышают напряжения от монтажных нагрузок [3, 7, 8]). В связи с этим на огневой поверхности ГЦ могут появиться трещины, что приведет к нарушению работоспособности ГЦ [9–11]. В работах [2, 3] была подробно рассмотрена методика расчета напряженно-деформированного состояния ГЦ под действием силовых нагрузок, которые возникают при изготовлении и сборке. Как показал расчет МКЭ [2, 3], при работе дизеля 4ЧН 10,5/12 (Д-145Т) на режиме максимального крутящего момента на огневой поверхности ГЦ температурные напряжения в перемычке между клапанами равны 108,1 МПа, в то время как напряжения от давления газов и нагружения при сборке составляют только 31,1 МПа, т.е. отличаются в три раза. Таким образом, именно теплонапряженное состояние ГЦ определяет её долговечность.
Рассмотрим порядок расчета теплонапряженного состояния ГЦ транспортного дизеля жидкостного охлаждения с учетом циклов нагрева и охлаждения в камере сгорания при его работе.
Цель исследования: разработать методику анализа теплового и напряженно-деформированного состояния ГЦ транспортного дизеля жидкостного охлаждения 8ЧН12/13 под действием монтажной нагрузки и сил давления газов, а также тепловых нагрузок, что позволит провести расчет ГЦ на долговечность и прогнозировать ее надежность в эксплуатации.
Мы не рассматриваем, как определять напряжения в ГЦ от газовых сил и монтажных нагрузок, так как это нами было изложено в работах [2, 3].
Известно, что на долговечность ГЦ влияют только низкочастотные колебания температуры, вызванные изменением режима работы двигателя [10, 11].
На основании исследований, приведенных в [12], дизели ЯМЗ-238, установленные на автомобилях КрАЗ-257 т КрАЗ-236Б, работают около 50–90 % времени на участке внешней скоростной характеристики при частоте вращения коленчатого вала 0,7–1 от номинальной.
На международном шоссе с асфальтобетонным покрытием число переключений скорости, а значит, и смена режима составляет 15–16 переключений на 100 километров пробега, в интенсивном городском движении таких переключений уже около 400 [12]. Для дизеля 8ЧН12/13 примем аналогичные смены режимов работы и учитывать при моделировании будем только низкочастотные колебания температуры.
Исходя из принятых допущений, циклограмму термонагружения ГЦ представим в виде, показанном на рис. 1. Из нее следует, что только переход на новый режим приводит к резкому росту температур в межклапанной перемычке, при этом уровень температур Tmax стабилизируется в течение τ наг. = 2–3 минуты после выхода дизеля на установившийся режим (рис. 1). Движение автомобиля при Tmax в течение τвыд.1 сопровождается колебанием нагрузки, однако существенного влияния на тепловой режим дизеля данное явление практически не оказывает и только остановка автомобиля приводит к снижению температур до уровня Tmin.
Для расчета МКЭ необходимо, основываясь на чертежах (рис. 2), создать трехмерную модель ГЦ с использованием программ твердотельного моделирования ANSYS, SolidWorks, Catia, Pro/Engineer и др.
Для расчета МКЭ механические характеристики материала ГЦ, направляющих втулок, седел клапанов и гильзы цилиндра в зависимости от температуры выбираются по справочным данным.
На основе разработанной трехмерной модели [2, 3] (рис. 3, а) создается конечно-элементная модель (КЭМ) c использованием программных комплексов конечно-элементного моделирования ANSYS или SolidWorks Simulation (рис. 3, б).
При построении КЭМ (рис. 3) необходимо использовать густую расчетную сетку и уменьшенные КЭ в сечениях перехода, например в перемычках между клапанами, а также в перемычках между отверстием под форсунку и выпускным клапанным отверстием ГЦ.
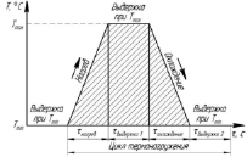
Рис. 1. Цикл термонагружения ГЦ
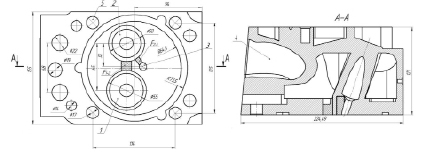
а) б)
Рис. 2. Головка цилиндров дизеля 8ЧН12/13: а) вид со стороны огневой поверхности ГЦ: 1 – впускной клапан; 2 – выпускной клапан; 3 – отверстие для установки форсунки, 4 – впускной канал; 5 – отверстия для шпилек крепления ГЦ; F1–2 – межклапанная перемычка; F2-f – перемычка между выпускным клапаном и стаканом форсунки; б) сечение по линии A–A
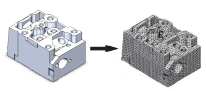
а) б)
Рис. 3. Процесс создания конечно-элементной модели: а) твердотельная 3D модель; б) конечно-элементная модель
При выборе кинематических граничных условий (ГУ) для КЭМ необходимо учитывать возможность перемещения поверхностей, связанных с блок-картером. По данным [19], исключение боковых перемещений поверхности КЭМ ГЦ дает погрешность в вычислении напряжений в перемычках между клапанами в 3–4 раза. Поэтому граничные условия назначаются в виде сил трения между ГЦ и опорной поверхностью блока [3].
Тепловые граничные условия (ГУ) при расчете теплонапряженного состояния ГЦ назначаются следующие:
ГУ I рода – задается распределение температуры на огневой поверхности S ГЦ как функция координат:
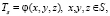(1)
где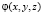 
– заданная на огневой поверхности ГЦ температура в узловых точках КЭ, полученная результатам термометрирования.
ГУ II рода – известно или задается распределение плотности теплового потока qs, проходящего через некоторую поверхность S:
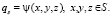(2)
Условие (2) можно записать в виде [6, 7]
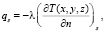(3)
где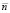 
– нормаль к поверхности тела S в некоторой точке с координатами x, y, z; λ – коэффициент теплопроводности материала ГЦ (Вт/(м×К)) [8, 10].
ГУ III рода – на поверхности тела задается плотность теплового потока вследствие теплопроводности со стороны тела от разности температур поверхности тела Ts и окружающей среды T∞ [4, 13, 1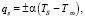4]:
(4)
где α – коэффициент теплоотдачи (теплообмена), Вт/(м2·К); TS, T∞ – температура в определенной точке огневой поверхности ГЦ и температура окружающей среды над этой точкой, 0K.
Коэффициент α характеризует интенсивность теплового взаимодействия среды заданной температуры T∞ с поверхностью тела [14–15].
Граничные условия III рода используются для решения стационарной задачи теплопроводности на огневой поверхности ГЦ.
На основании закона сохранения энергии с учетом (3) и (4) имеем
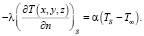(5)
Температурные поля фаски клапана и посадочной поверхности седла в ГЦ
Тепловые потоки за рабочий цикл дизеля меняют свое направление [4, 14, 15], поэтому при расчете температурных полей в ГЦ необходимо согласовывать температуру фаски клапана и посадочной поверхности седла. Когда клапаны закрыты, то все тепло передается на огневую поверхность ГЦ, от которой тепло передается впускному клапану. На такте впуска впускные клапаны омываются свежим зарядом, тем самым снижая температуру. На такте выпуска – клапаны и седло клапана омываются отработавшими газами, что поднимает их температуру. По разности температур поверхности их Ts и отработавших газов T∞ по плотности теплового потока и коэффициента теплоотдачи двух тел αк Вт/(м2•K) можно найти распределение температуры.
В работе [14] рекомендуется определять коэффициент теплоотдачи контакта двух тел αк Вт/(м2•K) по формуле [4, 20]:
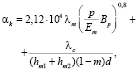(6)
где λm и Em – средние коэффициент теплопроводности и модуль упругости двух контактирующих тел (в нашем случае сплава алюминия и чугуна), которые определяются по формулам [4, 14]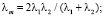 
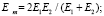p – контактное давление после запрессовки; Bp = 0,15–0,25 – безразмерный коэффициент, характеризующий геометрические свойства контактирующих поверхностей; λс ≈ 0,35·10-3 Вт/(м·град) – теплопроводность среды в объемах микронеровностей; m – коэффициент заполнения профиля микронеровностей (для шлифованных поверхностей m = 0,5); d ≈ 1,2–1,6 – коэффициент, характеризующий влияние максимальных выступов микронеровностей, зависящий от соотношения p/E [13].
При определении теплового и напряженно-деформированного состояния ГЦ [4, 10] необходимо проводить раздельный расчет седла и выпускного клапана. Для этого при первом итерационном расчете выбирается произвольная температура их и коэффициент теплоотдачи от клапана к седлу. Последовательным расчетом на каком-то этапе итерации эти температуры выравниваются. При открытых клапанах температуры и коэффициенты теплоотдачи клапана и седла усредняются. После нескольких итераций после выравнивания температуры фаски клапана и посадочной поверхности седла проводят расчет температурного поля ГЦ [4, 10].
Выбор граничных условий на огневом днище ГЦ
Обычно для определения среднего по огневой поверхности ГЦ значения коэффициента теплоотдачи используют формулы Вошни или Хохенберга [4, 15]. В работе [15] показано, что ни одна из зависимостей не позволяет получить удовлетворительные результаты. В связи с этим предлагается для расчета усредненного коэффициента теплоотдачи αГ в КС в процессе газообмена использовать формулу Цапфа [15]:
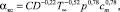(7)
где C = 535; T∞ – текущая температура рабочего тела в цилиндре, К; cm – средняя скорость поршня; p – текущее давление в цилиндре, МПа.
За время протекания цикла температура среды усредняется по всему объему КС.
Примем, что закон изменения коэффициента теплоотдачи от центра огневого днища ГЦ по радиусу в первом приближении будет таким же, как на огневом днище поршня [22, 23]. Тогда изменение усредненного за цикл локального коэффициента теплоотдачи αг по радиусу цилиндра r для дизелей с открытыми камерами сгорания [10, 15]:
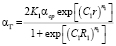при r ≤ R1; (8)
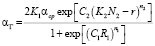при r > R1, (9)
где K1 – отношение среднего по поверхности днища ГЦ коэффициента теплоотдачи к среднему значению коэффициента теплоотдачи по всей поверхности КС.
Эмпирические коэффициенты K2, n1, n2, C1, C2, N2 определяются по заданным значениям αгmin, αг max, αг var соответственно на радиусах r = 0, r = R1, r = 0,5D (рис. 4).
При n1 = n2 = n справедливы следующие зависимости:
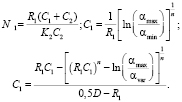
Распределение αг на огневом днище ГЦ дизеля 8ЧН12/13 по радиусу цилиндра представлено на рис. 4.
Граничные условия во впускных и выпускных каналах
При работе двигателя значительное количество теплоты подводится от отработавших газов к стенкам выпускного канала. Граничные условия во впускных и выпускных каналах можно представить через число Нуссельта [15], представляющее собой безразмерный коэффициент теплоотдачи:
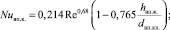(10)
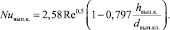
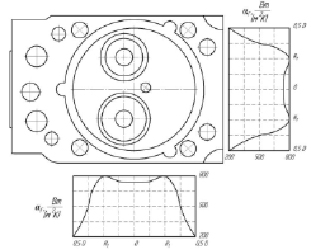
Рис. 4. Изменение коэффициента теплоотдачи на огневом днище ГЦ дизеля 8ЧН12/13 по радиусу цилиндра (для расчетов R1 = 32,5 мм – расстояние между центрами впускного и выпускного каналов)
В выражениях (10) h и d – ход клапанов и диаметры клапанов (с соответствующими индексами: вп – впускной; вып – выпускной). Для вычисления числа Рейнольдса определяющими размерами являются гидравлические диаметры каналов и средняя скорость потоков во впускном и выпускном каналах:
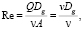(11)
где Q – объемный расход газа, м3/с; Dg – гидравлический диаметр канала, м; ν – кинематическая вязкость газа, м2/с; A – площадь сечения канала, м2; v – характерная скорость м/с.
Переход к коэффициентам теплоотдачи α осуществляется по известной зависимости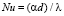 
, где λ – теплопроводность газа.
Расчет напряжений в сопряжении седло – головка цилиндров с учетом натяга и при нагреве был подробно рассмотрен нами в работе [2].
Теплообмен со стороны охлаждающей жидкости
Для расчета коэффициента теплоотдачи αж, Вт/(м2•K) со стороны охлаждающей жидкости [10, 15] можно использовать формулу Зоннекена:
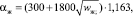(12)
где wж – скорость движения охлаждающей жидкости.
В качестве оценочных показателей теплового состояния огневого днища ГЦ примем:
- максимальную температуру на огневой поверхности ГЦ Tmax;
- температуры на кромках отверстий в выделенных зонах F1-2 и F2-f (рис. 2);
- максимальные температуры перемычек в тех же зонах;
- максимальный перепад температур по всей нагреваемой поверхности днища ГЦ;
- разность максимальных температур перемычки между выпускными и впускными каналами.
Для напряженно-деформированного состояния ГЦ примем следующие оценочные показатели:
- максимальное значение интенсивности напряжений σmax на поверхности огневого днища;
- интенсивность напряжений в соответствующих точках зон днища;
- наибольшая разность прогибов у кромок отверстий на днище под впускной и выпускной каналы.
В пределах каждого КЭ скалярное поле температур и векторное поле перемещений описываются полиномами второго порядка; напряжения изменяются линейно. Функция формы КЭ параболическая, что позволяет при одинаковой точности расчета применять значительно меньше элементов, чем при использовании тетраэдральных элементов [3].
Для получения матриц теплопроводности и жесткости объемного КЭ, а также соответствующих им векторов правых частей может быть применена четырнадцатиточечная кубаторная формула численного интегрирования, которая снизила время счета по сравнению с двадцатисемиточечной на 20 %.
Для решения задачи теплопроводности вычисляется матрица теплопроводности и вектор тепловой нагрузки каждого элемента, на основании которой формируется общая матрица и вектор «тепловой нагрузки» всей расчетной схемы. Температура во всех узловых точках расчетной схемы определяется после решения полученной системы линейных уравнений.
Так как алюминиевый сплав АК5М7 (АЛ10В), из которого изготовлена ГЦ, изменяет свои физико-механические характеристики в зависимости от температуры, то для уточнения коэффициента теплопроводности λ и модуля упругости E проводились их пересчеты в зависимости от температуры. Для реализации этого метода диапазон изменения температур ГЦ разбивался на десять интервалов, для которых можно принять λ = const, E = const.
Средняя температура в каждом КЭ перед пересчетом может быть определена по формуле
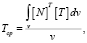(13)
где [N]T – транспонированный вектор функций формы элементов; [T] – вектор-столбец узловых температур элемента; v – объем элемента.
После этого в той же расчетной схеме учитываются принятые нами оценочные показатели теплового состояния, монтажных и газовых нагрузок [2] определяются компоненты перемещений во всех узловых точках. Далее поэлементный расчет напряжений позволяет определить тензор напряжений в любой точке ГЦ.
По известным компонентам тензора напряжений в узлах определяется интенсивность напряжений [2, 6]:
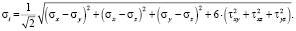(14)
Результаты расчетов и выводы
Несмотря на довольно значительное число исследований по определению коэффициента теплоотдачи [22], значения их, полученные по эмпирическим зависимостям, сильно отличаются. При расчете тепловой задачи в нестационарной постановке единственным способом решения задачи является усреднение температур и коэффициентов теплоотдачи по времени.
По результатам расчетов по приведенным зависимостям коэффициент теплоотдачи на огневом днище ГЦ около αг = 800 Вт/(м2·K) (в районе межклапанной перемычки – 775 Вт/(м2·K)).
На режиме максимального крутящего момента наибольшая температура огневой поверхности ГЦ дизеля 8ЧН12/13 составляет 345 °С в межклапанной перемычке. Температура ГЦ стороны охлаждения равна 175 °С. Температура посадочной поверхности седла выпускного клапана составляет 450 °С. При дальнейшем форсировании дизеля по среднему эффективному давлению необходимо предусмотреть меры по совершенствованию конструкции ГЦ.
Библиографическая ссылка
Гоц А.Н., Клевцов В.С. МЕТОДИКА РАСЧЕТА ТЕПЛОНАПРЯЖЕННОГО СОСТОЯНИЯ ГОЛОВКИ ЦИЛИНДРОВ ДИЗЕЛЯ ЖИДКОСТНОГО ОХЛАЖДЕНИЯ // Современные наукоемкие технологии. – 2020. – № 5. – С. 26-32;URL: https://top-technologies.ru/ru/article/view?id=38027 (дата обращения: 21.11.2024).