Теория передачи сигналов в стохастическом информационном канале получила интенсивное развитие благодаря разработке новых аналитических методов расчета случайных волновых полей [1]. Что касается прогнозирования характеристик сигналов в реальных каналах, то на данном пути возникает ряд проблем [2]. Прежде всего, это связано с тем, что при решении прикладных задач параметры стохастической структуры канала зачастую неизвестны, либо известны с малой долей вероятности. В этих условиях надежный расчет ожидаемых статистических характеристик сигналов при связи между корреспондентами затруднителен. Одним из вариантов решения данной проблемы является предварительное определение параметров стохастической структуры канала по характеристикам принятого пробного сигнала на некоторой реперной трассе, подобной по своим свойствам заданной трассе. Для решения обратной задачи на реперной трассе вначале необходимо получить функциональные соотношения, связывающие характеристики пробного сигнала и параметры случайных неоднородностей канала. Несмотря на то, что эти соотношения достаточно сложны, решение обратной задачи здесь возможно за счет упрощения модели неоднородной структуры канала. В данном направлении был получен ряд важных результатов, благодаря описанию поля случайных неоднородностей с помощью многопараметрической модели гауссова корреляционного эллипсоида [3]. Однако определение всех параметров эллипсоида требует большого числа измеряемых статистических характеристик сигнала и в общем случае неоднозначно.
Обратная задача на реперной трассе решается в настоящей работе для модели эффективного корреляционного эллипсоида с малым числом параметров, характеризующей более общие свойства стохастической структуры среды канала и допускающей простое обращение функциональных соотношений между характеристиками реперного сигнала и параметрами случайного поля неоднородностей. Обобщенные параметры поля неоднородностей, восстановленные таким образом, представляют и самостоятельный интерес, поскольку они содержат интегральную информацию о статистической изменчивости канала. Найденные параметры эллипсоида, выраженные через характеристики принятого реперного сигнала, в дальнейшем используются в качестве входных параметров в алгоритме расчета статистических характеристик основного сигнала на заданной трассе. Рассмотрена возможность непосредственного использования параметров реперного сигнала для расчета ожидаемых характеристик основного сигнала в пункте назначения.
Цель работы заключается в создании методики оценки ожидаемых статистических траекторных характеристик сигнала в информационном канале по данным измерений траекторных моментов пробного сигнала на реперной трассе.
Основные теоретические соотношения
Для надежной и качественной передачи информации корреспонденту, находящемуся на заданном расстоянии от источника, необходимо знать ожидаемые флуктуации характеристик принятого сигнала в пункте назначения. Среди измеряемых характеристик большое значение имеют статистические моменты фазы, групповой задержки и доплеровского смещения частоты сигнала. Наиболее просто эти характеристики можно рассчитать в приближении геометрической оптики [4]. Очевидно, что для расчета флуктуаций характеристик сигнала необходимо знать параметры и свойства случайно-неоднородной среды канала, соединяющего корреспондентов.
Пусть ε(x, z, τ) – пространственно-временная случайная функция диэлектрической проницаемости, описывающая возмущенную среду канала. В лучевом приближении для совместного расчета фазы, групповой задержки и доплеровского сдвига частоты сигнала соответственно имеем стохастические интегралы по траектории:
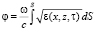 ,
, 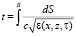 ,
,
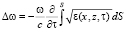 , (1)
, (1)
где τ – время, ω – циклическая частота, c – скорость света, dS – элемент дуги траектории, соединяющей корреспондентов и являющейся решением системы уравнений
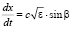 ,
, 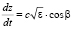 ,
,
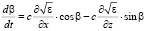 , (2)
, (2)
где x, z – текущие координаты луча, β – угол рефракции, dt – элемент групповой задержки.
Расчет флуктуаций траекторных характеристик проведем в приближении метода возмущений [5]. Для функций, входящих в уравнения (1), (2), используем разложения: 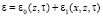 , φ = φ0 + φ1, t = t0 + t1, Δω = Δω0 + Δω1, S = S0 + S1, x = x0 + x1, z = z0 + z1, β = β0 + β1. Подставляя эти разложения в (1), (2) и проводя линеаризацию при условии
, φ = φ0 + φ1, t = t0 + t1, Δω = Δω0 + Δω1, S = S0 + S1, x = x0 + x1, z = z0 + z1, β = β0 + β1. Подставляя эти разложения в (1), (2) и проводя линеаризацию при условии 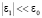 , в нулевом приближении имеем
, в нулевом приближении имеем
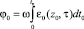 ,
,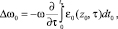 (3)
(3)
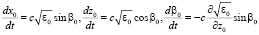 (4)
(4)
соответственно, для поправок первого порядка малости:
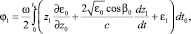 (5)
(5)
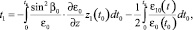 (6)
(6)
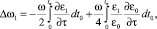 (7)
(7)
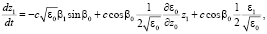 (8)
(8)
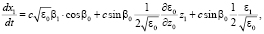 (9)
(9)
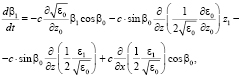 (10)
(10)
где x0, z0, β0, φ0, t0, Δω0, x1, z1, β1, φ1, t1, Δω1 – средние и флуктуационные характеристики сигнала; tк – групповая задержка сигнала в пункте назначения xк, функция ε0 – описывает среднюю диэлектрическую проницаемость канала, ε1 – случайные возмущения. Важно отметить, что флуктуация текущей траектории z1(t0), входящая в интегралы (5), (6), должна удовлетворять граничным условиям: z1(0) = z1(tк) = 0.
Для расчета флуктуации z1(t0) используем выражение, полученное в результате решения краевой траекторной задачи [6, 7]:
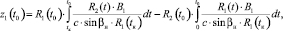 (11)
(11)
где βн – угол входа луча в канал 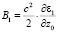 ,
, 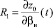 ,
, 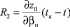 . Подставляя (11) в (5), (6) и считая
. Подставляя (11) в (5), (6) и считая 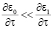 , после аналитических преобразований, имеем
, после аналитических преобразований, имеем
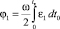 ,
, 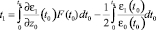 ,
, 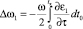 , (12)
, (12)
где 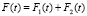 ,
, 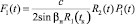 ,
, 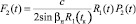 ,
,
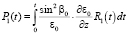 ,
, 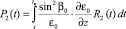 .
.
На основе (12) составим статистические моменты сигнала, принятого в пункте xк:
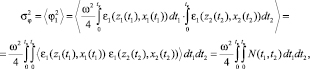 (13)
(13)
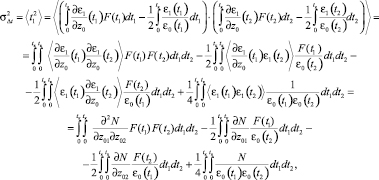 (14)
(14)
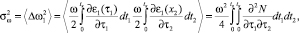 (15)
(15)
где 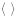 – знак усреднения по ансамблю неоднородностей канала,
– знак усреднения по ансамблю неоднородностей канала, 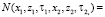
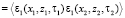 – функция корреляции флуктуаций диэлектрической проницаемости. Рассмотрим условия квазиоднородного случайного поля неоднородностей канала, когда N = N1N0. Здесь N0 – однородная часть корреляционной функции. Функция N1 характеризует статистическую неоднородность случайного поля неоднородностей и учитывает непостоянство параметров неоднородностей в канале. Далее в качестве функции N1 рассмотрим зависимость
– функция корреляции флуктуаций диэлектрической проницаемости. Рассмотрим условия квазиоднородного случайного поля неоднородностей канала, когда N = N1N0. Здесь N0 – однородная часть корреляционной функции. Функция N1 характеризует статистическую неоднородность случайного поля неоднородностей и учитывает непостоянство параметров неоднородностей в канале. Далее в качестве функции N1 рассмотрим зависимость 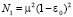 , где μ2 – интенсивность неоднородностей канала. Движение неоднородностей учтем в рамках гипотезы о переносе замороженной турбулентности [8]:
, где μ2 – интенсивность неоднородностей канала. Движение неоднородностей учтем в рамках гипотезы о переносе замороженной турбулентности [8]: 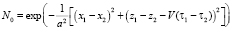 , где a – масштаб возмущений, V – скорость движения поля неоднородностей. Считая, что функция N1 изменяется более медленно, чем N0, интегралы (13)–(15) можно преобразовать, используя метод метод суммарно-разностного интегрирования [8]:
, где a – масштаб возмущений, V – скорость движения поля неоднородностей. Считая, что функция N1 изменяется более медленно, чем N0, интегралы (13)–(15) можно преобразовать, используя метод метод суммарно-разностного интегрирования [8]:
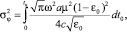
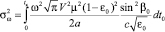 , (16)
, (16)
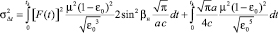 . (17)
. (17)
Диагностика состояния канала
Для расчета ожидаемых траекторных моментов сигнала по формулам (16), (17) необходимы параметры корреляционного эллипсоида μ2, V, a, которые в общем случае неизвестны, но их можно определить, решая обратную задачу на некоторой подобной (реперной) трассе. Источник реперного сигнала может находиться на некотором расстоянии от пункта назначения основного сигнала, а пункт приема реперного сигнала совпадает с пунктом излучения основного сигнала. На рис. 1 приведены возможные реперные трассы для основной трассы, длиной хк = 1200 км. Расчеты выполнены в однослойном канале, средняя диэлектрическая проницаемость которого задана функцией: 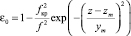 , где zm, ym, fкр – высота минимума, полутолщина и критическая частота слоя. Параметры модели составляли: zm = 300 км, ym = 150 км, fкр = 7 МГц. Рабочая частота f = 12 МГц.
, где zm, ym, fкр – высота минимума, полутолщина и критическая частота слоя. Параметры модели составляли: zm = 300 км, ym = 150 км, fкр = 7 МГц. Рабочая частота f = 12 МГц.
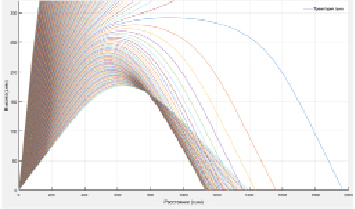
Возможные реперные трассы в диэлектрическом информационном канале для дистанции между корреспондентами хк = 1200 км
Для определения параметров корреляционного эллипсоида используем вышеприведенные аналитические расчеты. В частности, для дисперсий траекторных характеристик сигнала на реперной трассе хр имеем
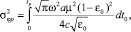
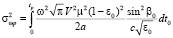 , (18)
, (18)
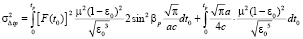 . (19)
. (19)
где βр – угол входа реперного сигнала в канал. Решая уравнения (18), (19) относительно неизвестных параметров неоднородностей, имеем
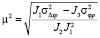 ,
, 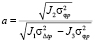 ,
, 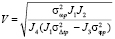 , (20)
, (20)
где
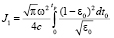 ,
, 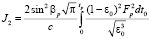 , (21)
, (21)
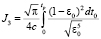 ,
, 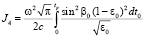 . (22)
. (22)
Подставляя (20) в (16), (17) и проводя аналитические преобразования, имеем
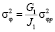 ,
, 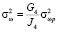 ,
,
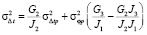 , (23)
, (23)
где
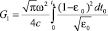 ,
,
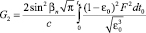 , (24)
, (24)
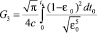 ,
,
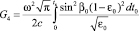 . (25)
. (25)
Задавая средний высотный профиль диэлектрической проницаемости канала, формулы (23) можно использовать для оценки ожидаемых статистических траекторных характеристик сигнала на заданной трассе хк по данным измерений траекторных моментов на реперной трассе хр. Из формул (21)–(25), в частности, имеем, что при малом отличии заданной и реперной трасс, когда tp > tк, интегралы G1 > J1, G2 > J2, G3 > J3, G4 > J4, и соответственно дисперсии 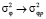 ,
, 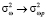 ,
, 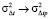 , что является следствием теоремы взаимности [9].
, что является следствием теоремы взаимности [9].
Заключение
На основе приближения геометрической оптики и метода возмущений получены функциональные соотношения, связывающие усредненные стохастические интегралы для основных траекторных характеристик реперного сигнала с параметрами корреляционной функции, описывающей статистически неоднородное случайное поле неоднородностей канала. Используемая модель пространственной зависимости неоднородной части корреляционной функции самосогласованна с изменением средней диэлектрической проницаемости канала и учитывает динамику степени возмущенности канала на трассах различной протяженности. При расчетах моментов траекторных характеристик учтены флуктуации траектории, возникающие при решении стохастической траекторной задачи с граничными условиями в пунктах излучения и приема реперного сигнала. Полученные функциональные соотношения для моментов траекторных характеристик на реперной трассе решены относительно конечного числа неизвестных параметров эффективного корреляционного эллипсоида при известных измеренных дисперсиях фазы, групповой задержки и доплеровского сдвига частоты принятого реперного сигнала в пункте излучения основного сигнала. Разработана оперативная методика оценки ожидаемых статистических характеристик основного сигнала в возмущенном информационном канале по известным параметрам хаотических неоднородностей канала, выраженным через измеренные дисперсии основных траекторных характеристик пробного сигнала на реперной трассе.
Библиографическая ссылка
Агеева Е.Т., Афанасьев Н.Т., Багинов А.В., Ким Д.Б., Танаев А.Б., Чудаев С.О. ДИАГНОСТИКА СОСТОЯНИЯ ИНФОРМАЦИОННОГО КАНАЛА ПО СТАТИСТИЧЕСКИМ ТРАЕКТОРНЫМ ХАРАКТЕРИСТИКАМ РЕПЕРНОГО СИГНАЛА // Современные наукоемкие технологии. 2020. № 5. С. 9-14;URL: https://top-technologies.ru/ru/article/view?id=38024 (дата обращения: 08.01.2026).
DOI: https://doi.org/10.17513/snt.38024



