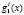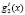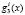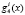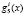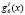В последние годы разработчики проектов, связанных с глобальным освоением территорий Российской Федерации, расположенных за Полярным кругом, особое внимание уделяют низкоорбитальным системам спутниковой связи (НССС). Это связано с тем, что только НССС способны обеспечить обмен данными между абонентами, которые находятся в районах Крайнего Севера [1]. При этом современные низкоорбитальные системы спутниковой связи должны иметь высокую помехозащищенность, которая базируется на информационной, структурной и энергетической скрытностях. В работах [2, 3] показано, что использование систем опознавания спутника «свой – чужой» позволяет повысить информационную скрытность НССС. При этом построение протокола аутентификации на основе параллельных вычислений с применением полиномиальных модулярных кодов (ПМК) обеспечивает сокращение времени необходимого на вычисление статуса спутника. Кроме того, ПМК позволяют системам опознавания сохранять работоспособное состояние при выходе из строя нескольких вычислительных трактов. Но при этом необходимо пересчитывать значения ортогональных базисов, которые применяются в Китайской теореме об остатках (КТО) при выполнении обратного перевода из ПМК в позиционную систему счисления (ПСС). Поэтому разработка метода вычисления динамически изменяемого кортежа ортогональных базисов является актуальной задачей.
Применение полиномиальных модулярных кодов в системах опознавания «свой – чужой» позволяет решить следующие задачи. Во-первых, это повышение производительности проверки статуса спутника за счет применения параллельных методов вычислений [3]. Во-вторых, это повышение отказоустойчивости путем коррекции ошибок в процессе функционирования за счет введения избыточности в ПМК. В-третьих, это возможность системы опознавания сохранять работоспособное состояние при выходе из строя нескольких вычислительных трактов за счет перераспределения оставшихся вычислительных ресурсов. Но при реконфигурации системы опознавания, реализованной с использованием ПМК, необходимо производить пересчет ортогональных базисов для работоспособных оснований. Цель исследования – разработать метод вычисления динамически изменяемого кортежа ортогональных базисов, применение которого позволит обеспечить сохранение работоспособного состояния системы опознавания при постепенной деградации основных показателей в заданных пределах.
Материалы и методы исследования
Полиномиальные модулярные коды являются непозиционными кодами, в которых числа А, представленные в виде многочленов А(х), задаются кортежем остатков [4]. То есть в виде
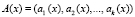, (1)
где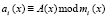 
; 
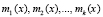– основания ПМК, в качестве которых выбираются неприводимые многочлены; 
.
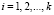Произведение кортежа оснований дает рабочий диапазон
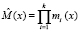. (2)
Использование ПМК позволяет осуществлять параллельные вычисления согласно
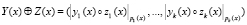, (3)
где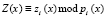 
; 
– операции модульного сложения и умножения.
В работе [3] был представлен протокол аутентификации спутника, который использует полиномиальные модулярные коды. В работе показано, что это позволило сократить временные затраты на проверку статуса спутника. Но согласно [4] полиномиальные модулярные коды могут повысить отказоустойчивость устройства. Чтобы исправить ошибку, возникшую в одном остатке, необходимо два контрольных модуля
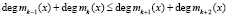. (4)
Однако в процессе длительного использования отказы в системе опознавания могут накапливаться. С целью противодействия такой последовательности отказов ПМК предлагают провести отключение отказавших вычислительных трактов (оснований). В этом случае динамически изменяется кортеж оснований ПМК, а это требует вычисления новых значений ортогональных базисов. При этом наибольшие сложности связаны с вычислением веса ортогонального базиса gi(z).
Известно, что обратное преобразование ПМК-ПСС реализуется на основе КТО
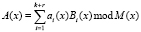, (5)
где Вi(х) – ортогональный базис;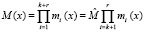 
– полный диапазон ПМК.
При этом ортогональные базисы определяются следующим образом:
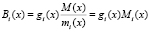, (6)
где gi(z) – вес базиса Вi(х);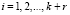 
; r – количество контрольных оснований.
Значение Mi(x) достаточно просто вычисляется для любого кортежа оснований. При этом необходимо определить вес ортогонального базиса gi(x) для выполнения условия
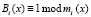. (7)
В работе [5] для вычисления динамически изменяемого кортежа ортогональных базисов предлагается сначала определить значение
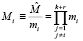. (8)
После этого реализуется выражение для вычисления остатка
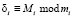, (9)
с помощью которого определяется мультипликативно обратный элемент – вес базиса:
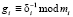, (10)
Проведенный анализ показал, что этот метод требует значительных вычислительных затрат. Устранить данный недостаток позволяет разработанный метод пересчета базисов.
Если решить, что ортогональный базис можно вычислить, используя равенство
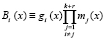, (11)
то справедливо выражение
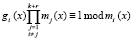. (12)
Разделим обе стороны последнего равенства на константу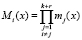 
. Тогда
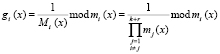. (13)
Так как в модулярных полиномиальных кодах основаниями являются взаимно простые неприводимые многочлены, то вес ортогонального базиса будет определяться
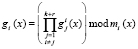. (14)
где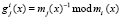 
; 
.
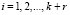Результаты исследования и их обсуждение
Рассмотрим разработанный метод, используя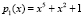 
, 
, 
, 
, 
, 
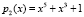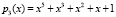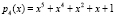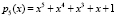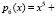
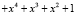. В таблице приведены константы 
.
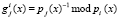Константы для вычисления веса ортогонального базиса
|
Основания mi(x) полиномиального модулярного кода |
||||||
|
р1(x) |
р2(x) |
р3(x) |
р4(x) |
р5(x) |
р6(x) |
|
|
|
– |
x2 + x |
x4 + x3 + x2 + x |
x + 1 |
x4 + x3 + 1 |
x4 + x3 + x2 |
|
|
x2 + x + 1 |
– |
x3 + x2 + 1 |
x4 |
x4 + x3 + x |
x + 1 |
|
|
x4 + x3 + 1 |
x3 + x2 |
– |
x4 + x2 |
x3 |
x4 |
|
|
x |
x4 + x3 + x + 1 |
x4 + x3 + x2 + x + 1 |
– |
x4 + x3 |
x2 + x |
|
|
x4 + x2 |
x4 + 1 |
x3 + x2 + x + 1 |
x4 + x3 + x2 + x + 1 |
– |
x3 + x |
|
|
x4 + 1 |
x |
x4 + x3 + x2 + 1 |
x2 + x + 1 |
x3 + x + 1 |
– |
Пусть кортеж ПМК состоит из полиномов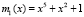 
, 
, 
, 
, 
.
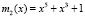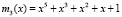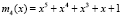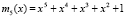Вычислим вес ординального базиса В1(х). Для этого необходимо найти произведение констант, которые располагаются в первом столбце таблицы. Тогда получаем
.
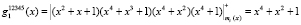Выполним проверку с использованием [черв].
1. 
.
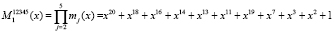2. 
.
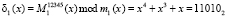3. 
.
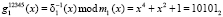Используя разработанный метод, вычислим оставшиеся веса базисов ПМК
,
,
,
.
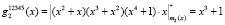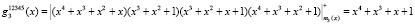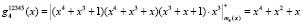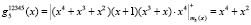Пусть в процессе функционирования из строя последовательно вышли два первых основания. После их отлучения ПМК состоит из оснований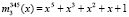 
, 
, 
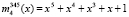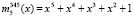, где верхний индекс показывает оставшиеся работоспособные основания. Используя разработанный метод, вычислим веса динамически изменившегося кортежа ортогональных базисов ПМК
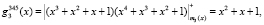
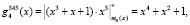
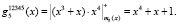
Выполним проверку с использованием [черв].
1. Вычислим константы согласно (8). Получаем
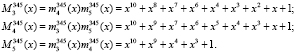
2. Вычислим остатки констант согласно (9). Тогда
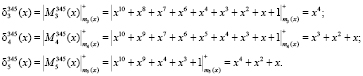
3. Вычислим веса ортогональных базисов согласно (10). Получаем
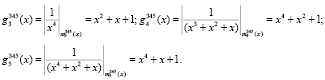
Тогда пересчитанные ортогональные базисы равны
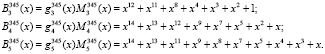
Проверка ортогональных базисов
.
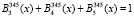Анализ разработанного метода показал, что для получения веса базиса необходимо выполнить (n* – 1) операцию умножений, где n* – количество работоспособных оснований ПМК, которые можно выполнять параллельно с вычислением констант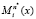 
. А при использовании метода [5] необходимо сначала выполнить (n* – 1) операцию умножений для вычислений констант 
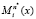, затем одну операцию деления и вычисления веса с использованием LUT-таблицы. В работе [6] показано, что для выполнения операций умножение/деление необходимо 4 такта, а на команду типа регистр-память 6 тактов CPU. В этом случае при пересчете кортежа из трех ортогональных базисов метода [5] потребуется 18 тактов CPU, что при использовании процессора Intel(R) Core™ i5-3470 CPU соответствует 5,625 нс. А разработанный метод для этого потребует 8 тактов CPU, затратив на это 2,5 нс, что в 2,25 раз меньше.
Заключение
Применение ПМК в протоколе аутентификации спутника позволяет не только снизить временные затраты на опознавание, но и повысить отказоустойчивость системы «свой – чужой». При этом ПМК позволяют системе опознавания сохранять работоспособное состояние при выходе из строя нескольких вычислительных трактов за счет перераспределения оставшихся вычислительных ресурсов. Но при реконфигурации системы опознавания, реализованной с использованием ПМК, необходимо производить пересчет ортогональных базисов. В работе представлен разработанный метод вычисления динамически изменяемого кортежа ортогональных базисов, применение которого требует в 2,25 раз меньше временных затрат по сравнению с методом, приведенным в работе [5].
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-07-01020.
Библиографическая ссылка
Калмыков И.А., Степанова Е.П., Калмыкова Н.И., Павлюк Д.Н., Слюсарев Г.В. РАЗРАБОТКА МЕТОДА ВЫЧИСЛЕНИЯ ДИНАМИЧЕСКИ ИЗМЕНЯЕМОГО КОРТЕЖА ОРТОГОНАЛЬНЫХ БАЗИСОВ, ПОЗВОЛЯЮЩЕГО ПОВЫСИТЬ ОТКАЗОУСТОЙЧИВОСТЬ СИСТЕМЫ ОПОЗНАВАНИЯ СПУТНИКА // Современные наукоемкие технологии. – 2020. – № 4-2. – С. 223-227;URL: https://top-technologies.ru/ru/article/view?id=38000 (дата обращения: 19.04.2024).