Испытания различных изделий промышленного производства в общем случае классифицируются по следующим этапам: 1) испытания на стадии проектирования 2) испытания на стадии доводки, 3) производственные испытания, 4) испытания на стадии эксплуатации, 5) ремонтные испытания. Для автоматизации испытаний высокотехнологичных изделий используют специализированные программно-технические комплексы и испытательные станции [1, 2].
В ходе проектирования и доводки изделий организуют доводочные, предварительные и приемочные испытания. К стадии производства относят квалификационные, предъявительские, приемосдаточные, периодические, инспекционные, типовые, аттестационные, сертификационные испытания. Поэтому испытания промышленных изделий в потоке воздуха могут быть применены на любом из перечисленных этапов промышленного производства.
Необходимость использования потока воздуха при производстве испытаний промышленных изделий вызывается, в частности, тем, что требуется имитировать условия внешней среды, в которых эти изделия должны функционировать. В качестве примеров можно привести испытания авиационных планеров в потоке воздуха, квадрокоптеров, испытания воздуховодов и вентиляторов, испытания изделий при повышенной температуре, испытания при повышенном давлении, определение ветровых нагрузок здания [3, 4], определение обтекаемости и воздушного сопротивления автомобилей [5], электротехнических изделий [6], конструкций самолетов [7, 8] и авиационных двигателей [9], ракетно-космической техники и другой специальной техники.
Для того чтобы проводить испытания различных изделий в потоке воздуха, требуется управлять процессом испытаний. Эта функция возлагается на систему автоматизации испытаний (САИ). С помощью САИ должны формироваться требуемые параметры воздушного потока вблизи испытуемого объекта (ИО). Для реализации такого управления требуется априорная информация о поведении воздушного потока, эта информация содержится в математической модели воздушного потока. Поэтому целью исследований является получение математической модели воздушного потока. Для достижения цели решается задача идентификации модели воздушного потока.
Задача идентификации модели воздушного потока
Воздушный поток, необходимый для испытания промышленных изделий, может быть описан с помощью упрощенной математической модели, которая должна быть удобна для таких задач, как диагностика в процессе испытаний, разработка управляющих устройств испытательных установок, синтез алгоритмов управления. Позже упрощенная модель идентифицируется на основе экспериментальных данных.
На рис. 1 показана схема испытаний, при которой формируется заданное давление (P), заданная температура воздуха (t, K), заданная скорость воздуха (V), которую в свою очередь можно описать через геометрию трубы и массовый расход воздуха.
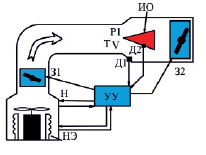
Рис. 1. Схема испытаний. Обозначения: ИО – испытуемый объект, З – заслонка (управляющий элемент), Н – нагнетатель, НЭ – нагревательный элемент, Д – датчик, УУ – устройство управления испытательной установки
Нагнетатель с нагревательными элементами НЭ создает поток воздуха, который управляется с помощью З1, затем по воздуховоду поступает в камеру с испытуемым изделием, в камере создается заданная температура, давление, расход и скорость воздуха. Может применяться добавочная заслонка (управляющий элемент) на выходе (З2), датчики могут устанавливаться как на самом ИО (Д2), так и в камере, где ИО размещен (Д1). Устройство управления получает информацию с датчиков и передает ее на управляющие органы, как правило, УУ связано также с пультом управления оператора. Главная задача установки – сформировать требуемые давление, температуру, расход воздуха и скорость воздуха в соответствии с заданной программой испытаний ИО. Нагнетатель выполняет функцию вентилятора или компрессора, разгоняет воздух и формирует давление, помимо этого в нагнетателе устанавливаются нагревательные элементы (НЭ), чтобы управлять температурой воздуха.
Математические модели нагнетателя с нагревающим элементом и испытуемого объекта, как объектов управления, построены с учетом основных физических взаимосвязей. Статические характеристики, обеспечивающие соответствие модели экспериментальным данным, берутся из серии экспериментов [10].
Постоянные времени, отражающие инерционность процессов, определяются как время необходимое для достижения 0,63 от становившегося значения при подаче управляющего воздействия [11]. Наряду с этим постоянные времени затем уточняются с помощью метода наименьших квадратов [11, 12].
Упрощенную модель потока воздуха в соответствии с рис. 1 представим системой уравнений:
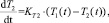 (1)
(1)
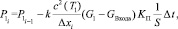 (2)
(2)
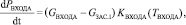 (3)
(3)
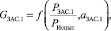 (4)
(4)
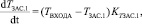 (5)
(5)
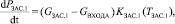 (6)
(6)
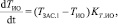 (7)
(7)
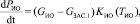 (8)
(8)
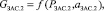 (9)
(9)
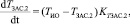 (10)
(10)
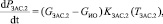 (11)
(11)
где Ti – температура в заданном сечении i (K), Pi – давление в заданном сечении (Па), Gi – расход воздуха в сечении i (кг/с), αЗАС.i – угол положения заслонки i, KT.i – коэффициент пропорциональности температуры в сечении i, зависящий от расстояния, KП – коэффициент перевода из Па в кгс/см2, c – скорость звука, зависящая от температуры (м/с), Δxi – расстояние (м), S – площадь сечения воздуховода (м2), k – поправочный коэффициент, полученный с помощью метода наименьших квадратов, Ki(Ti) – коэффициент пропорциональности между давлением и расходом воздуха, зависящий от температуры и расстояния.
Для реализации процедуры идентификации вначале требуется выбрать и обосновать метод оценивания определяемых параметров модели. Достоинства и недостатки традиционных методов оценивания хорошо известны и детально рассмотрены уже в классическом труде П. Эйкхофа (1974 г.) [11]. Там же даны рекомендации, в каких случаях целесообразно применять тот или иной метод. Проще всего, особенно на первом этапе исследований, использовать классический метод наименьших квадратов, так как он в общей постановке задачи идентификации не требует никакой априорной информации о модели исследуемого объекта [11, 12]. Для других методов оценивания из [11] (использование байесовских оценок; метод максимального правдоподобия; использование марковских оценок; взаимно-корреляционный метод; метод стохастической аппроксимации) необходима не просто априорная информация, но информация статистическая, что требует дополнительных затрат времени и порой бывает малодоступно для непосредственной реализации.
Метод наименьших квадратов (МНК) также не свободен от недостатков. В рамках рассматриваемой задачи наибольшие проблемы вызывают такие его свойства, как смещенность оценки, если среднее значение случайных возмущений является ненулевым. Также здесь необходимо иметь всю информацию о входе и выходе на всем промежутке времени оценивания. Еще одним недостатком классического МНК является то, что он в силу свой универсальности связывает входы и выходы между собой, не заботясь о достоверности физических соотношений. Поэтому получаемая в результате такой идентификации модель может оказаться очень далека от физической сущности процессов, протекающих в объекте исследований. На помощь здесь приходит условная оценка наименьших квадратов, с помощью нее возможно принудительно задать те или иные взаимосвязи между переменными модели и ее параметрами, присвоить отдельным параметрам фиксированные значения.
Определение коэффициентов модели методом наименьших квадратов
Для оценки коэффициентов полученной упрощенной модели воздушного потока разработан алгоритм идентификации с использованием метода наименьших квадратов.
Покажем на наглядном примере работу данного алгоритма идентификации.
Даны следующие уравнения и зависи- мости:
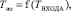 (12)
(12)
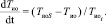 (13)
(13)
В уравнениях (12) и (13) приняты обозначения:
ТВХОДА – температура на входе трубо- провода;
ТИО – температура на испытуемом объекте;
ТИОS – температура на испытуемом объекте установившаяся;
TИО_t – постоянная времени температуры испытуемого объекта.
Необходимо определить значение постоянной времени температуры испытуемого объекта.
Дифференциальное уравнение (13) можем привести к следующему виду:
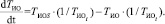 (14)
(14)
Заменив 1/ TИО_t на a11 и a12, получаем следующий вид уравнения:
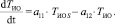 (15)
(15)
Дальше введем параметр ТВХОДА в уравнение (15) вместо ТИОS и получим следующий вид уравнения:
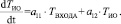 (16)
(16)
Для удобства записи все коэффициенты в уравнении стоят со знаком «+», это совершенно не скажется на работе алгоритма, так как в ходе работы коэффициенты примут соответствующие им знаки.
Приведем уравнение (16) к стандартному векторно-матричному описанию для непосредственного использования в процедуре оценивания МНК, для этого обозначим производную 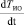 в качестве вектора выходных переменных Y, тогда переменные ТВХОДА, ТИО образуют вектор входных переменных X, в этом случае а11 и а12 составят матрицу коэффициентов, которую следует идентифицировать.
в качестве вектора выходных переменных Y, тогда переменные ТВХОДА, ТИО образуют вектор входных переменных X, в этом случае а11 и а12 составят матрицу коэффициентов, которую следует идентифицировать.
В результате уравнение (16) будет выглядеть как
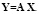 (17)
(17)
Из уравнения (17) с помощью МНК непосредственно вычисляется матрица А:
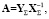 (18)
(18)
где YΣ и XΣ – матрицы, составленные из 2 векторов Y и X соответственно.
Поскольку наблюдений используется значительно больше чем n = 2, то применяется следующая оценка методом наименьших квадратов:
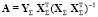 (19)
(19)
или
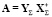 ,
,
где матрица 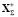 является псевдообратной матрицей:
является псевдообратной матрицей: 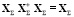 [11].
[11].
По условиям задачи, так как модель строится на основе экспериментальных данных, у нас есть массив ТВХОДА и ТИО. Производная ТИО ищется просто, по четырем точкам, так как время каждого снятия точки нам известно, то найти Δt не составит труда. Матрица коэффициентов А находится единожды для данного массива данных.
Необходимо убедиться, что в ходе алгоритма коэффициенты были найдены правильно, для этого надо провести моделирование, используя матрицу коэффициентов А и сравнивая полученные результаты имитационного моделирования с экспериментальными данными.
При получении векторно-матричного уравнения (17) в качестве выходного вектора принимался одномерный вектор производной ТИО. Возникает вопрос, как формировать вектор YΣ, составленный из n > 2 наблюдений за изменением производной ТИО? Приходится предварительно вычислять производную как разность соседних значений ТИО, деленную на шаг наблюдений. Точность определения производной может быть повышена за счет использования большего числа точек, но это вызывает свои трудности с алгоритмизацией.
Поэтому многие авторы советуют преобразовать уравнение (17) к разностному (дискретному) виду:
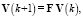 (20)
(20)
где V(k) – расширенный вектор состояния системы в k-й момент времени, V(k + 1) – расширенный вектор состояния системы в k + 1-й момент времени, F – матрица перехода из состояния в момент k в новое состояние в момент k + 1, 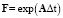 , Δt – промежуток времени между моментами времени k и k + 1. Алгоритм идентификации при определении матрицы F представлен на рис. 2.
, Δt – промежуток времени между моментами времени k и k + 1. Алгоритм идентификации при определении матрицы F представлен на рис. 2.
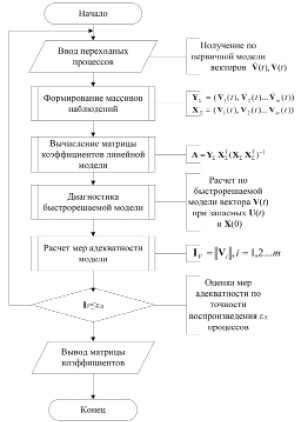
Рис. 2. Алгоритм идентификации
Аналогичным образом, с помощью алгоритма идентификации могут быть определены коэффициенты для уравнения (3). Раскрыв скобки, получаем следующее уравнение:
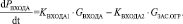 (21)
(21)
Далее, заменяя KВХОДА на a11 и a12, получим уравнение в форме (17). Идентификацию можно проводить непосредственно по нему или предварительно перейти к уравнению (20) и воспользоваться алгоритмом, представленным на рис. 2.
Рассмотренный алгоритм идентификации позволяет определить по экспериментальным данным параметры модели воздушного потока (1–11).
Описание программно-моделирующего комплекса
В рамках проведения работ по идентификации параметров модели был разработан программно-моделирующий комплекс (ПМК), позволяющий проводить параметрическую идентификацию для нахождения коэффициентов дифференциальных уравнений, а также выполнять процедуру получения модельных данных на основе этих коэффициентов. В состав ПМК входят основные модули:
1) модуль чтения данных из файлов;
2) модуль формирования переменных и уравнений;
3) модуль идентификации;
4) модуль моделирования.
Модуль чтения данных из файлов преобразует данные в удобный для работы формат. Модуль формирования переменных и уравнений позволяет выбрать структуру уравнений пользователю. Модуль идентификации проводит параметрическую идентификацию выбранных уравнений. Модуль моделирования позволяет провести моделирование идентифицированных уравнений и создать новые данные, которые могут быть построены с помощью вспомогательного модуля построения графических характеристик. При наличии необходимого набора экспериментальных данных и информации о структуре уравнений, ПМК позволяет без каких-либо усилий выполнить идентификацию.
Выводы
Для идентификации математической модели воздушного потока используется метод наименьших квадратов, поскольку мы обладаем полной информацией по входу и выходу, однако существует недостаток априорной информации. Недостатки данного метода могут привести к неточностям математической модели, однако модель останется пригодна для использования в качестве основы для проверки существующих устройств управления.
Для процесса идентификации представлен алгоритм идентификации, а также описан программно-моделирующий комплекс, помогающий идентифицировать модель по существующим наборам экспериментальных данных.
Библиографическая ссылка
Опарин Д.А., Бахирев И.В., Кавалеров Б.В., Килин Г.А. О ПРОЦЕДУРЕ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ВОЗДУШНОГО ПОТОКА // Современные наукоемкие технологии. 2020. № 3. С. 70-75;URL: https://top-technologies.ru/ru/article/view?id=37943 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.37943



