Современные задачи оптимизации получили широкое распространение в исследовании технических, технологических и экономических систем и процессов. Они содержат большое количество параметров с различными видами ограничений и сложное описание критерия оптимальности. Эффективным вариантом поиска экстремального значения целевой функции являются не только классические методы решения с использованием дифференциального исчисления, но и стохастические методы, которые представляют собой эвристический способ поиска искомого набора значений параметров путем случайного подбора, комбинирования и изменения их значений с помощью генетических алгоритмов [1, 2].
Идея применения генетических алгоритмов состоит в том, чтобы смоделировать законы эволюции живой природы в процессе решения задач оптимизации. Описание теории генетических алгоритмов впервые было представлено в работе Джона Холланда [3]. Начало развития этого направления в Советском Союзе связано с исследованиями Л.А. Растригина [2]. Генетические алгоритмы успешно используются при решении различных оптимизационных задач по автоматизации информационных систем [4] и по улучшению показателей бизнес-процессов [5], изменению транспортной инфраструктуры [6], фильтрации результатов тематического поиска документов [7].
Основной проблемой математического моделирования механизма работы генетических алгоритмов является корректное преобразование значений параметров целевой функции с учетом диапазона их возможных значений, так как их произвольное изменение может привести к возникновению недопустимых решений.
Целью представленного исследования выступает формализация комбинирования разнообразных вариантов допустимых решений задачи оптимизации для отбора наилучшего решения, обеспечивающего достижение экстремального значения целевой функции.
Результаты исследования и их обсуждение
Получаемые с помощью генетических алгоритмов допустимые решения задачи оптимизации представляются в виде одномерных массивов параметров. Каждому элементу массива соответствует свой индекс и диапазон возможных значений. Длина массива определяется количеством искомых параметров задачи оптимизации. Процесс решения задачи начинается с формирования генератором случайных чисел заданного множества одномерных числовых массивов. После этого вычисляются значения целевой функции для каждого массива и производится целенаправленный отбор лучших массивов по требуемым критериям. Нахождение наилучшего решения задачи достигается согласованной работой трех операторов: оператора селекции, оператора бинарной рекомбинации (скрещивания) и оператора мутации. Работа генетического алгоритма включает многократное прохождение однотипных действий или циклов.
Оператор селекции на основе логического сравнения значений целевой функции [1–3] выбирает два массива параметров: наилучший и самый близкий к нему. Отобранные с помощью оператора селекции два массива подвергаются случайным изменениям операторами бинарной рекомбинации и мутации. Оператор бинарной рекомбинации позволяет получить новые массивы значений параметров путем взаимного обмена элементами из двух лучших наборов параметров. Если выбирается одна точка обмена элементов, то такой оператор называется одноточечным, если две точки, то двухточечным, а если больше двух, то многоточечным [1–3]. Оператор мутации преобразует один из двух ранее выбранных массивов. Он осуществляет перестановки его отдельных элементов с заданными индексами. Если выбирается один индекс элемента, то такой оператор мутации называется одноточечным, если два индекса, то двухточечным, а если больше двух, то многоточечным [1–3].
При случайном определении оператора мутации могут возникнуть такие перестановки элементов внутри массива, которые приведут к тому, что переставленные параметры не будут принадлежать диапазонам своих возможных значений. Это может привести к получению недопустимых решений задачи оптимизации. Одним из вариантов решения данной проблемы выступает кодирование всех искомых параметров в виде двоичного кода [4]. Недостатком этого подхода является большая длина массива параметров, что увеличивает время работы генетического алгоритма.
Интересным вариантом устранения появления недопустимых решений является замена оператора мутации оператором вариации, который изменяет значение выбранного случайным образом элемента массива на определенную величину таким образом, чтобы изменяемое значение параметра не превышало его диапазон. Расположение параметра в массиве остается прежним.
Первый цикл работы генетического алгоритма содержит только массивы параметров, полученные с помощью генераторов случайных чисел. Второй и последующие циклы содержат три группы массивов: массивы, полученные с помощью оператора бинарной рекомбинации, массивы, полученные с помощью оператора вариации и вновь сформированные массивы с помощью генераторов случайных чисел. Для массивов всех трех групп вычисляются значения целевой функции, и производится отбор оператором селекции двух лучших наборов параметров. Результатом работы генетического алгоритма выступает массив значений параметров с экстремальным значением целевой функции, полученный на последнем цикле. Блок-схема такого генетического алгоритма с оператором вариации представлена на рисунке.
Наиболее простой моделью генетических алгоритмов является генетический алгоритм с одноточечным оператором бинарной рекомбинации и одноточечным оператором вариации. В этом случае используется меньшее количество генераторов случайных чисел. Рассмотрим работу генетического алгоритма с одноточечными операторами бинарной рекомбинации и вариации.
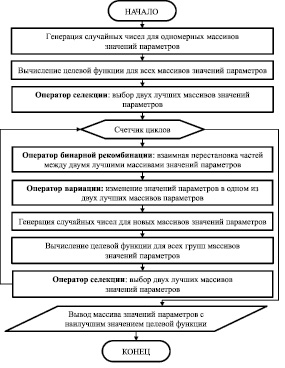
Блок-схема генетического алгоритма с оператором вариации
Введем следующие обозначения: l – количество параметров задачи оптимизации; αk – минимальное значение k-го параметра задачи оптимизации (k = 1,…, l); βk – максимальное значение k-го параметра задачи оптимизации (k = 1,…, l); N – количество циклов генетического алгоритма; Npop – количество массивов параметров в каждом цикле; Wij – j-й массив значений параметров i-го цикла (i = 1,…, Npop, j = 1,…, N); wijk – k-й параметр j-го массива в i-м цикле (k = 1,…, l, i = 1,…, Npop, j = 1,…, N); L(Wij) – целевая функция задачи оптимизации; Wi* – лучший массив параметров в i-м цикле; Wi** – самый близкий к лучшему массив параметров в i-м цикле; Nbr – количество массивов параметров, формируемых с помощью оператора бинарной рекомбинации в одном цикле; b – точка оператора бинарной рекомбинации (номер параметра в массиве); Nvar – количество массивов наборов параметров, формируемых с помощью оператора вариации в одном цикле; v – точка оператора вариации (номер параметра в массиве); Nnew – количество массивов параметров, формируемых с помощью генератора случайных чисел в каждом цикле кроме первого.
Пусть генетический алгоритм имеет N циклов. В первом цикле выполняются действия: 1) генерация случайных чисел для одномерных массивов; 2) вычисление целевой функции для всех массивов параметров; 3) выбор двух лучших массивов наборов на основе оператора селекции. Во втором и последующих циклах выполняются такие действия как: 1) взаимное преобразование двух лучших массивов на основе оператора одноточечной бинарной рекомбинации; 2) изменение значений элементов одного из двух выбранных массивов на основе оператора одноточечной вариации; 3) генерация случайных чисел для новых одномерных параметров; 4) вычисление целевой функции для массивов всех групп; 5) выбор двух лучших массивов значений параметров на основе оператора селекции.
Элементы wijk одномерного массива определяются с помощью генератора случайных чисел по формуле
wijk = αk + F(ηk)(βk – αk), k = 1,2,…, l, (1)
где F(ηk) – функция распределения непрерывной случайной величины ηk. Вид функции F(ηk) определяется условием задачи и ее начальными данными. Формируется Npop массивов на первом цикле.
На каждом цикле на основе оператора селекции выбираются массивы Wi* и Wi**, которым соответствуют значения целевой функции L(Wi*)ext и L(Wi**)δext на i-м цикле. Оператор одноточечной бинарной рекомбинации [1] позволяет получить новые массивы Wij путем взаимного обмена элементами массивов Wi-1* и Wi-1**, разделенных на две части, на i-м цикле. Один цикл генетического алгоритма может содержать Nbr массивов Wij, полученных с помощью этого оператора. Работа оператора одноточечной бинарной рекомбинации определяется вычислением точки кроссинговера n случайным образом и преобразованием массивов Wi-1* и Wi-1** путем обмена элементов между ними.
Значение точки оператора одноточечной бинарной рекомбинации можно найти по формуле
b = Fbr(ψ)l, (2)
где Fbr(ψ) – функция распределения дискретной случайной величины ψ. Вид функции Fbr(ψ) определяется условием задачи и ее начальными данными.
Элементы одномерных массивов Wij определяются по формуле
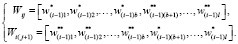 (3)
(3)
Если в генетическом алгоритме присутствует оператор двухточечной бинарной рекомбинации, то элементы одномерных массивов Wij будут определяться по формуле
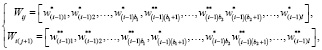 (4)
(4)
где b1, b2 – точки оператора двухточечной бинарной рекомбинации.
Оператор одноточечной вариации создает массив Wij путем изменения на заданную величину какого-либо одного элемента из массива Wi-1* или из массива Wi-1**. Один цикл генетического алгоритма содержит Nvar массивов Wij, полученных с помощью оператора одноточечной вариации. Работа оператора одноточечной вариации определяется следующими действиями: 1) выбором одного из лучших массивов Wi-1* или Wi-1**; 2) вычислением точки вариации v случайным образом, 3) установление значения случайной величины q, определяющей знак; 4) преобразование выбранного лучшего массива путем изменения z-ого элемента на заданную величину Δv.
Значение точки оператора одноточечной вариации осуществляется по формуле:
v = Fvar(ξ)l, (5)
где Fvar(ξ) – функция распределения дискретной случайной величины. Вид функции Fvar(ξ) определяется условием задачи и ее начальными данными.
Величина q, определяющая знак, принимает значения 0 или 1. Ее можно вычислить, используя генератор случайных чисел с равномерным законом распределения с параметрами 0 и 1. Если сгенерированное число будет меньше 0,5, то значение q принимается равным 0. Если сгенерированное число будет больше 0,5, то значение q принимается равным 1. Если в первом действии был выбран лучший массив Wi-1*, то значения его элементов можно найти следующим образом:
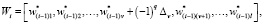 (6)
(6)
где q – случайная величина, определяющая знак; Δv – величина изменения v-го параметра нечеткого регулятора. Если в первом действии будет выбран массив Wi-1**, то его преобразование будет аналогично формуле (6).
Если в генетическом алгоритме присутствует оператор двухточечной вариации, то элементы одномерного массива Wij будут определяться по формуле
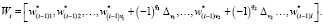 (7)
(7)
где v1, v2 – точки оператора двухточечной вариации; q1, q2 – случайные величины, определяющие знак.
Второй и последующие циклы генетического алгоритма содержат Nnew массивов значений параметров Wij, полученных с помощью генераторов случайных чисел. Количество таких массивов можно найти по формуле
Nnew = Npop – Nbr – Nvar – 2. (8)
Автоматизацию работы предложенного генетического алгоритма можно осуществить в среде MATLAB. Данная среда обладает высокоуровневым интерпретируемым языком программирования, включающим широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования [8]. Для организации работы генетического алгоритма используются следующие компоненты среды MATLAB: генераторы случайных чисел, условный оператор, оператор цикла, система имитационного моделирования Simulink, функции сортировки элементов массива.
Встроенный генератор случайных чисел позволяет формировать массивы Wij, определять точки операторов бинарной рекомбинации и вариации, выбирать один из двух лучших массивов для случайных преобразований. Условный оператор if используется в работе операторов бинарной рекомбинации и вариации для осуществления выбора одного из двух лучших массивов. Оператор цикла for используется для организации перехода между циклами генетического алгоритма.
Система имитационного моделирования Simulink используется для вычисления значения целевой функции L(Wij). Она моделирует работу сложных систем управления при решении задач оптимизации. Функция сортировки элементов массива sort применяется для реализации процесса селекции.
Примером задачи оптимизации с большим количеством параметров выступает синтез нечеткого регулятора для системы управления с несколькими управляемыми величинами и одним управляющим воздействием. Предложенная схема работы генетического алгоритма реализована в компьютерной программе для синтеза нечеткого регулятора [9]. Эффективность разработанной программы рассмотрена на примере задачи управления динамической стабилизацией неустойчивого равновесия перевернутого маятника [10].
Заключение
Замена оператора мутации оператором вариации в генетическом алгоритме для решения задачи оптимизации с различными ограничениями для параметров позволяет формировать новые значения параметров с учетом их диапазона. Важным преимуществом предложенного оператора вариации является возможность учитывать особенности диапазона каждого параметра целевой функции в отдельности. Если количество параметров целевой функции невелико, то можно использовать двухточечные и многоточечные операторы бинарной рекомбинации и вариации для достижения большего числа возможных сочетаний значений параметров.
Библиографическая ссылка
Куликова И.В. ПОСТРОЕНИЕ ГЕНЕТИЧЕСКОГО АЛГОРИТМА ДЛЯ РЕШЕНИЯ ЗАДАЧ ОПТИМИЗАЦИИ С РАЗЛИЧНЫМИ ОГРАНИЧЕНИЯМИ ДЛЯ ПАРАМЕТРОВ // Современные наукоемкие технологии. 2020. № 2. С. 40-44;URL: https://top-technologies.ru/ru/article/view?id=37912 (дата обращения: 07.01.2026).
DOI: https://doi.org/10.17513/snt.37912



