На Атырауском нефтеперерабатывающем заводе возникла задача увеличения межремонтного пробега установки гидроочистки прямогонного бензина с двух до трех лет [1, 2]. Одной из основных причин малого межремонтного пробега является неравномерная тепловая нагрузка на многозональную коробчатую печь, которая служит для нагревания промежуточных продуктов до температуры реакции.
Существующая на заводе печь, выполненная по проекту института «Ленгипрогаз», представляет собой коробчатую многозональную многокамерную конструкцию (рис. 1).
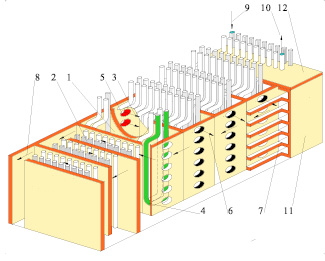
Рис. 1. Схема многокамерной трубчатой печи: 1 – радиантная камера, 2 – камера конвекции, 3 – радиантная секция, 4 – труба змеевика, 5 – горелка, 6 – выход дымовых газов из радиантной камеры, 7 – канал дымовых газов, 8 – выход газов из печи, 9 – вход сырья, 10 – выход сырья, 11 – стена печи, 12 – свод печи
Радиационно-конвективная часть печи состоит из камеры конвекции и пяти камер радиации. Теплообменная поверхность трубчатой печи [3] имеет вид змеевиков, выполненных в виде вертикальных петель, по которым движется нагреваемая жидкость. Внутренний объем печи разделен вертикальными стенками на две неравные части, из которых одна является камерой радиации (топочным пространством), а другая – камерой конвекции. В камере радиации смонтированы топливные форсунки. Количество форсунок в каждой из пяти камер – 6 шт., общее количество – 30 шт. Основной проблемой при эксплуатации печи является разрушение части труб из-за коксообразования и связанного с ним перегрева. Именно эти причины не позволяют повысить межремонтный пробег печи с двух до трех лет.
Повреждение труб змеевика представляет собой одну из наиболее серьёзных аварий печи [4]. Они работают в условиях высоких температур и значительных внутренних давлений. Как показывает статистический анализ наиболее часто возникающих дефектов змеевиков трубчатых печей [5, 6], прогар труб встречается примерно в 10–15 % случаев, несколько чаще встречаются дефекты, вызванные износом наружной поверхности – 18–20 %, износ внутренней поверхности и окалина являются причиной возникновения дефектов приблизительно в 10–15 % случаев, остальной процент аварий приходится на иные факторы (прогиб и т.п.).
Основной причиной прогара труб является перегрев металла в местах коксовых отложений. Средняя температура в радиантной камере примерно равна 800–900 °С, а в конвекционной камере – 500–600 °С [3]. Следовательно, стенки радиантных труб нагреваются до более высокой температуры, чем стенки конвекционных труб. Высокая температура поверхности трубопровода вызывает термическое разложение прилегающих к ней слоев жидкости с образованием кокса, отлагающегося на внутренней поверхности трубы. Интенсивность коксообразования зависит от температурного режима работы и от скорости движения продукта по трубам [5–7]. Чем выше температура и меньше скорость потока, тем интенсивнее коксообразование.
При турбулентном режиме движения жидкости по трубам вблизи стенок жидкость движется во много раз медленнее, чем в ядре потока. Чем выше шероховатость поверхности трубы и чем меньше скорость движения жидкости, тем больше толщина пограничного слоя. Этот слой подвергается интенсивному перегреву и термическому разложению с образованием кокса. Таким образом, основной задачей снижения коксообразования и, соответственно, повышения надежности работы печи является обеспечение равномерности полей температур, скоростей и интенсивности перемешивания в межтрубном пространстве радиационных и конвективной камер печи.
Целью настоящей работы являлось математическое моделирование полей скоростей и температур в горизонтальном и вертикальном сечениях радиантной камеры коробчатой печи для выявления зон перегрева и коксообразования.
В задачу численного эксперимента входило определение:
– максимальных температур на наружной стороне труб;
– неравномерности нагрева наружных стенок труб в радиантной камере коробчатой печи;
– приведенного коэффициента теплоотдачи от топочных газов к стенке трубы.
Исходными данными для расчета являлись габаритные размеры печи: длина 23,5 м; ширина 7,0 м; высота 11,2 м. Теплопроизводительность – 24440 кВт. Расход исходного сырья (прямогонный бензин) – 40200 кг/час. Максимальное давление на входе – 5 МПа.
Распределение труб и форсунок по камерам представлено в таблице.
Распределение труб и форсунок по камерам
|
Камера печи |
Количество труб |
Количество форсунок |
Диаметры труб, мм |
|
конвекционная |
60 |
– |
219х8 |
|
1-я радиантная |
20 |
6 |
108х8 |
|
2-я радиантная |
24 |
6 |
76х8 |
|
3-я радиантная |
24 |
6 |
76х8 |
|
4-я радиантная |
20 |
6 |
108х8 |
|
5-я радиантная |
14 |
6 |
108х8 |
Математическое моделирование полей скоростей и температур в многозональной печи
Для проведения газодинамических и тепловых расчетов печи был использован программный комплекс (ПК) FlowVision v 2.3 [8–10], предназначенный для решения трехмерных уравнений динамики жидкости и газа. ПК FlowVision позволяет проводить расчет сложных движений газа и жидкости, сопровождаемых дополнительными физическими явлениями, такими как турбулентность, горение, теплоперенос и т.п. В систему FlowVision можно импортировать геометрическую модель из любой CAD-системы трехмерного моделирования [8–10]. При построении физической модели процесса использовались уравнения движения однородной жидкости при различных скоростях с учетом эффектов сжимаемости, турбулентности и теплопереноса.
Применялась модель теплопереноса, обычно используемая в задачах сопряженного теплообмена для учета теплопереноса между жидкостью и твердым телом.
В модель включено уравнение энергии, записанное через энтальпию.
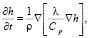(1)
где h – энтальпия; t – время; ρ – плотность; Cp – удельная теплоемкость; λ – коэффициент теплопроводности.
Использовали гидродинамическую модель слабо сжимаемой жидкости, описывающую движение газа при дозвуковых числах Маха и любых изменениях плотности [11]. В данной модели присутствовали уравнение Навье – Стокса
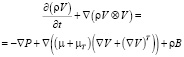(2)
и уравнение неразрывности
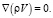(3)
Для моделирования турбулентного течения в данной задаче использовалась так называемая стандартная k-ε модель турбулентности [11–13], включающая в себя уравнения для переноса и диссипации турбулентной энергии:
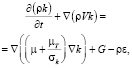(4)
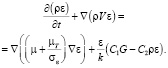(5)
В уравнениях (4) и (5) через G обозначено выражение
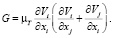(6)
Данная модель является полуэмпирической, и численные значения входящих в неё коэффициентов получены из экспериментальных данных [13]. Значения параметров k-ε модели равны σk = 1,0; σε = 1,3; Cμ = 0,09; C1 = 1,44; C2 = 1,92.
В уравнениях (2)–(7): V – вектор скорости; P – давление; μ – динамическая вязкость; B – силы тяжести и вращения (Кориолиса и центробежная).
Перенос теплоты в потоке описывается уравнением для энтальпии h:
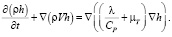(7)
Для моделирования процессов сжигания метана в горелках в присутствии воздуха применялась модель горения [8], основанная на уравнениях, которые описаны в модели слабо сжимаемой жидкости. В модель входили уравнения Навье – Стокса; уравнения для k и ε; уравнения состояния идеального газа; уравнения энергии; уравнения для скалярных величин ξ, описывающих концентрацию топлива, окислителя, продуктов сгорания и оксидов азота:
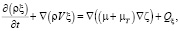(8)
где Qξ – массовый поток вещества.
Процесс горения представляется в виде брутто-реакции
1 кг топлива + i-кг окислителя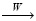 
(1 + i)-кг продуктов сгорания.
В зависимости от выбора скорости брутто-реакции W различают:
– модель Зельдовича (модель «что смешалось, то сгорело») [14], в которой скорость W предполагается бесконечно большой, а окислитель и горючее не существуют одновременно в одной точке пространства;
– кинетическую модель горения [8], в которой скорость W определяется кинетикой процесса, что справедливо при ламинарном течении смеси топлива и окислителя. В кинетической модели скорость брутто-реакции W выбирается в виде закона Аррениуса Wkin ;
– турбулентную модель горения [8], в которой скорость W определяется скоростью турбулентного смешения Wmix топлива и окислителя (эта модель справедлива для предварительно неперемешанных топлива и окислителя);
– пульсационную модель горения, где скорость W определяется уровнем относительных пульсаций γ, принимающих значение 0 при полностью перемешанном горючем и окислителе и значение 1 при неперемешанных компонентах [11]:
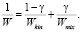(9)
При решении задачи использовалась также модель излучения в объеме. Она предполагает, что среда раскаленных газов поглощает и излучает электромагнитные волны инфракрасного, светового и ультрафиолетового диапазонов. В задаче использовалась диффузионная модель FlowVision [8], которая предполагает, что поле излучения изотропно, и дымовые частицы не влияют на радиационный перенос энергии.
Геометрическая модель внутренней полости камеры печи предварительно была построена с помощью системы Компас 3D и затем импортирована во FlowVision.
При построении геометрической модели весь исследуемый объем разбивался на две подобласти: внутреннюю полость печи, заполненную горячим газом (т.е. внутренний объем камеры за вычетом объема, занимаемого трубами змеевиков), и подобласть, занимаемую собственно трубами. Течение среды внутри труб не моделировалось, трубы задавались как твердые тела с внутренним стоком теплоты. Теплоперенос между стенкой трубы и нагреваемым продуктом учитывался в интегрированном виде в коэффициентах теплового сопротивления при постановке граничных условий (подробнее см. ниже).
Для уменьшения требуемых ресурсов компьютера (объема оперативной памяти и быстродействия) были использованы свойства продольной симметрии исследуемого объема. Строго говоря, в верхней части камеры трубы расположены не совсем симметрично относительно центральной плоскости, но это не сильно влияет на конфигурацию газовых потоков в камере. Полный объем камеры был разбит на несколько объемов меньшего размера вертикальной и горизонтальной плоскостями. Один из таких расчетных объемов показан на рис. 2.
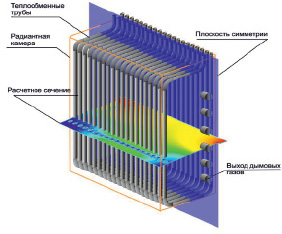
Рис. 2. Положение расчетного сечения, для которого строились слои визуализации
Постановка задачи численного моделирования
В области межтрубного пространства задавалась модель слабосжимаемой жидкости (по терминологии FlowVision) совместно с моделями теплопереноса и излучения газа. В качестве рабочей среды задавались смесь продуктов сгорания углеводородсодержащего газа с учетом избытка воздуха 15 %.
При этом принимали начальные значения температуры газа в камере – T0 = 900 °С; начальную степень турбулизации потока – b = 0,03.
Степень турбулизации потока оценивалась параметром b, который входит в уравнение для оценки кинетической энергии турбулентности k, приведенной к характерной скорости потока Vm:
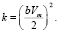(10)
Параметр b используется для задания начальных и граничных условий. При b < 0,03 наблюдается слабая турбулизация потока; при 0,03 < b < 0,05 – средняя турбулизация потока; при 0,05 < b < 0,1 – высокая турбулизация потока.
Для задания начальных и граничных условий для скорости диссипации турбулентности ε использовался масштаб турбулентности (характерный размер вихря). Для внутренних течений он обычно выбирается как 1/10 характерного размера входного сечения, для внешнего обтекания принимается как 1/10 характерного размера обтекаемого тела. В нашем случае масштаб турбулентности – l = 0,5 м.
В качестве граничных условий на стенке принимали нулевой поток теплоты. Внешнюю теплоизоляцию считали идеальной и потерями теплоты через кирпичную футеровку пренебрегали.
Коэффициент черноты, который используется в расчете переноса теплоты излучением, для футеровки из огнеупорного кирпича может быть принят равным 0,85 [15].
Граничное условие для скорости – ламинарный пограничный слой с логарифмическим профилем. Значение шероховатости для футеровки из огнеупорного кирпича принимали равным 1,0 мм.
На стенке трубы змеевика в качестве граничного условия для температуры было принято условие для теплового потока с сопротивлением. Это граничное условие используется в тех случаях, когда к стенке расчетной области примыкает прослойка (в нашем случае – стенка трубы плюс имеющие тепловое сопротивление загрязнения), которая может быть заменена тепловым сопротивлением.
Среднюю температуру среды внутри труб принимали равной 500 °С, общий коэффициент теплопереноса считали равным 12 Вт/(м2·К). По данным [15], коэффициент черноты для окисленной стали может быть принят равным 0,8.
Граничное условие для скорости – ламинарный пограничный слой с логарифмическим профилем. Значение шероховатости для окисленной стали принимали равным 0,1 мм.
На плоскости симметрии для всех параметров в качестве граничного условия задаем условие симметрии.
Граничное условие для температуры на входе в камеру: входная температура продуктов сгорания топлива 950 °С, что соответствует температуре дымовых газов на выходе из радиантной камеры 820 °С. Коэффициент черноты = 0 [15].
Граничное условие для скорости на входе в камеру – нормальный массовый поток (поток массы, приведенный к площади входного патрубка) равен 0,63 кг/(м2·с).
В качестве граничных условий на входе в камеру для турбулентной энергии задаем начальную степень турбулизации потока b = 0,03. В качестве граничных условий для энергии диссипации турбулентности задаем масштаб турбулентности l = 0,1 м.
Граничные условия на выходе из камеры: для температуры – нулевой поток; лля скорости – свободный выход; для турбулентной энергии и энергии диссипации турбулентности – нулевой поток. Коэффициент черноты = 0 [15].
Результаты численного эксперимента и их обсуждение
В результате численного эксперимента получены распределения скоростей и давлений жидкости во всех точках расчетного пространства, что позволило оценить эффективность конструкции. На рис. 2 показано положение расчетного сечения, для которого строились слои визуализации. В данное сечение попадают вертикальные участки змеевиковых труб.
На рис. 3 приведено распределение скоростей в горизонтальном сечении радиантной камеры, на рис. 4 – поле температур в том же сечении. На рис. 5 показано распределение скоростей в вертикальном сечении радиантной камеры; на рис. 6 – поле температур в том же сечении.
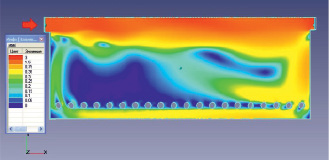
Рис. 3. Распределение скоростей в горизонтальном сечении. Слой визуализации – заливка из абсолютного значения скорости
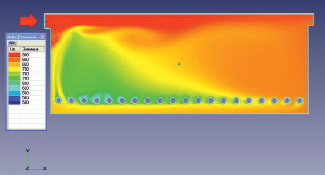
Рис. 4. Поле температур в горизонтальном сечении радиантной камеры
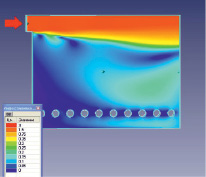
Рис. 5. Распределение скоростей в вертикальном сечении радиантной камеры
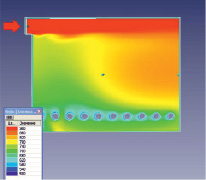
Рис. 6. Поле температур в вертикальном сечении радиантной камеры
Как видно из рис. 3 и 5, течение газов в камере отличается крайней неравномерностью. В центральной области образуется несколько вихревых зон, при этом факел раскаленных газов проходит по центральной части камеры и растекается по противоположной стенке. Это приводит к возникновению возвратного течения вдоль стенки между вертикальной стенкой и трубами змеевика. В результате вблизи труб, расположенных ближе к горелкам, формируется ярко выраженная застойная зона, простирающаяся до середины камеры (рис. 3). На рис. 3 показана заливка слоя по скорости газа, из которой видно, что в застойной зоне скорости газа чрезвычайно малы – менее 0,05 м/с.
На рис. 4 и 6 показано распределение температур в горизонтальном и вертикальном сечениях камеры. Распределение температур также отличается большой неравномерностью. Видно, что наихудшие условия наблюдаются на вертикальных участках змеевиковых труб. Расчетные значения максимальных и минимальных температур наружных стенок змеевиковых труб (нумерация труб на рисунках идет слева направо):
– максимальная температура равна 645 °С – труба № 20;
– минимальная температура равна 514 °С – трубы № 2 – 4.
Заключение
Результаты численного эксперимента отчетливо продемонстрировали, что в области расположения крайних труб температура в камере намного превышает среднюю. Возможен перегрев крайних труб, который может вызвать повышенное коксообразование на их стенках со всеми вытекающими негативными последствиями – прогаром и разрушением.
Выявление застойных зон, а также зон перегрева труб змеевиков позволяет наметить пути реконструкции исследуемой печи с целью увеличения межремонтного пробега.
Работа выполнена при поддержке госзадания Министерства науки и высшего образования Российской Федерации.
Библиографическая ссылка
Иваненко А.Ю., Яблокова М.А., Пономаренко Е.А., Грабская Н.В. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МНОГОКАМЕРНОЙ ПЕЧИ УСТАНОВКИ ГИДРООЧИСТКИ БЕНЗИНА С ЦЕЛЬЮ ОПРЕДЕЛЕНИЯ ЗОН ПЕРЕГРЕВА И КОКСООБРАЗОВАНИЯ // Современные наукоемкие технологии. – 2020. – № 2. – С. 12-19;URL: https://top-technologies.ru/ru/article/view?id=37907 (дата обращения: 21.11.2024).