Будем называть цифровыми двойниками некие психологические компьютерные аналоги человека. Отличие роботов с неабсолютной памятью от цифровых двойников состоит в том, что роботу задаются «психологические» параметры самими разработчиками робототехнической системы, а для цифровых двойников приближенно вычисленные психологические параметры человека переводятся в робототехнические системы, функционирующие на основе математических моделей и алгоритмов роботов с неабсолютной памятью [1].
Опишем основные определения эмоционального воспитания цифровых двойников, описанные для роботов с неабсолютной памятью в работах [1–3].
В работах [1, 3] введено соотношение, позволяющее математически описывать непрерывное воспитание роботов с неабсолютной памятью. Это соотношение имеет вид
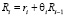 ,
,
где i – порядковый номер такта (порядковый номер эмоции, порожденной у робота при непрерывном воспитании), 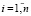 , n – количество непрерывных воспитательных тактов, ri – элементарное воспитание [1, 3] робота, полученное в результате воздействия на робота эмоции i, Ri – итоговое воспитание робота [1, 3] в конце такта i, где
, n – количество непрерывных воспитательных тактов, ri – элементарное воспитание [1, 3] робота, полученное в результате воздействия на робота эмоции i, Ri – итоговое воспитание робота [1, 3] в конце такта i, где 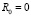
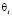 – коэффициент эмоциональной памяти робота с неабсолютной памятью, характеризующий запоминание предыдущих воспитаний робота в конце такта i,
– коэффициент эмоциональной памяти робота с неабсолютной памятью, характеризующий запоминание предыдущих воспитаний робота в конце такта i, 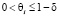 ,
, 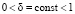 .
.
В работе [4] введено определение амбивалентных эмоций [5] робота, предполагающее одновременное возникновение у робота эмоций, противоположных по знаку. При этом воспитание робота 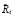 характеризуется вектором
характеризуется вектором 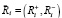 , где
, где 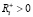 ,
, 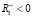 ,
, 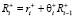 ,
, 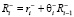 ,
, 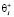 – коэффициент памяти, характеризующий запоминание положительной компоненты
– коэффициент памяти, характеризующий запоминание положительной компоненты 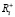 вектора амбивалентной эмоции
вектора амбивалентной эмоции 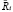 ,
, 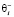 – коэффициент памяти, характеризующий запоминание отрицательной компоненты
– коэффициент памяти, характеризующий запоминание отрицательной компоненты 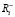 вектора амбивалентного воспитания
вектора амбивалентного воспитания 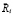 .
.
В работе [6] введено определение злопамятного и незлопамятного робота: если выполняется соотношение 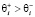 , то робот называется незлопамятным, если справедливо неравенство
, то робот называется незлопамятным, если справедливо неравенство 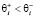 – злопамятным.
– злопамятным.
В работе [7] даны определения равномерно забывчивых роботов (выполнение условий 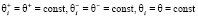 ). Если справедливы равенства
). Если справедливы равенства 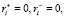 ri = 0, то соответствующие им такты, описывающие перерыв в воспитании, называются фиктивными тактами.
ri = 0, то соответствующие им такты, описывающие перерыв в воспитании, называются фиктивными тактами.
Целью настоящей статьи является создание математического метода, позволяющего определять злопамятность или незлопамятность цифрового двойника по известным численным значениям его воспитаний.
Математическая модель приближенного вычисления коэффициентов памяти злопамятных и незлопамятных цифровых двойников
В работе [6] приведено правило вычисления коэффициентов памяти, определяющих злопамятных или незлопамятных цифровых двойников на основе входных экспериментальных численных данных 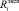 ,
, 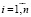 , описывающих их воспитание при фиктивных тактах, количество которых равно n.
, описывающих их воспитание при фиктивных тактах, количество которых равно n.
Пусть робот по каждому амбивалентному воспитанию является равномерно забывчивым, т.е. величины 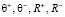 – каждая по отдельности – принимают только постоянные значения.
– каждая по отдельности – принимают только постоянные значения.
Для фиктивного такта с номером i значение отклонения экспериментального воспитания от расчетного воспитания зададим формулой
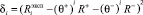 .
.
Очевидно, что для фиктивных тактов суммарное значение отклонения Δ экспериментальных воспитаний от расчетных удовлетворяет соотношению
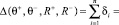
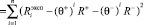 . (1)
. (1)
Очевидно, что для того, чтобы величины 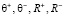 адекватно описывали воспитательный процесс при фиктивных тактах, величина Δ должна быть минимальна с учетом следующих ограничений:
адекватно описывали воспитательный процесс при фиктивных тактах, величина Δ должна быть минимальна с учетом следующих ограничений:
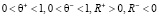 . (2)
. (2)
Используем метод Лагранжа [7] для определения условного экстремума функции (1) с ограничениями (2).
Стоит отметить, что для однозначного определения значений 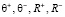 необходимо выполнение неравенства n ≥ 4.
необходимо выполнение неравенства n ≥ 4.
Для решения поставленной задачи разработана программа в пакете Mathematica [8]. Входными параметрами для программы является набор экспериментальных чисел 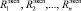 . На выходе программа возвращает значения
. На выходе программа возвращает значения 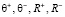 , для которых значение целевой функции Δ минимально.
, для которых значение целевой функции Δ минимально.
Приведем примеры определения значений 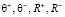 , полученные на основе разработанной программы по заданным экспериментальным значениям, измеренным у людей, например, с помощью компьютерной программы компании ELSYS [9].
, полученные на основе разработанной программы по заданным экспериментальным значениям, измеренным у людей, например, с помощью компьютерной программы компании ELSYS [9].
Пример 1
Для следующих значений воспитаний
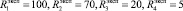
получены соответствующие значения 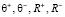 :
:
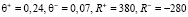 .
.
Согласно введенному выше определению можно сделать вывод о том, что цифровой двойник является незлопамятным.
Пример 2
Для численных значений входных параметров воспитаний робота
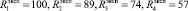
получены следующие значения 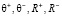 :
:
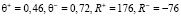
Этот цифровой двойник является зло- памятным.
Верификация модели натурными экспериментами позволяет сделать вывод о том, что предложенная методика определения злопамятных или незлопамятных людей на основе измеренных параметров воспитаний при фиктивных тактах позволяет получать верные результаты в 87 % случаев [6], т.е. эта оценка позволяет создавать равномерно забывчивых цифровых двойников по компонентам амбивалентных воспитаний с точностью 87 %.
В работе [10] на основе расчетов показано, что для равномерно забывчивых цифровых двойников с коэффициентом памяти θ равномерно забывчивых злопамятных двойников с коэффициентами памяти 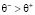 или незлопамятных двойников с коэффициентами памяти
или незлопамятных двойников с коэффициентами памяти 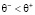 создать невозможно.
создать невозможно.
Математическая модель строгого вычисления коэффициентов памяти злопамятных и незлопамятных цифровых двойников
Решение задачи (1)–(2) позволяет приближенно определить злопамятность или незлопамятность цифрового двойника. В настоящем разделе предлагается более строгий метод определения этих психологических параметров двойника.
В работе [3] на основе использования программы [9] показано, что человек может успокаиваться только в течение четырех минут, что соответствует четырем фиктивным тактам. Через 4 минуты без внешних стимулов, но за счет каких-то внутренних факторов эмоциональное возбуждение человека увеличивается. В связи с этим для вычисления коэффициентов памяти достаточно использовать эмоциональные воспитания только четырех последовательно идущих друг за другом фиктивных тактов. Исходя из этого рассуждения, можно, начиная нумерацию фиктивных тактов с нуля, предположить справедливость следующей системы уравнений:
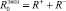 , (3)
, (3)
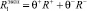 , (4)
, (4)
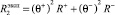 , (5)
, (5)
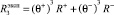 . (6)
. (6)
Очевидна справедливость следующей цепочки неравенств:
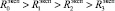 .
.
Легко видеть, что соотношения (3)–(5) влекут равенства
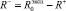 , (7)
, (7)
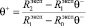 , (8)
, (8)
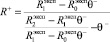 . (9)
. (9)
Подставляя соотношения (7)–(9) в формулу (6), получим уравнение для вычисления коэффициента памяти 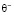 отрицательного воспитания:
отрицательного воспитания:
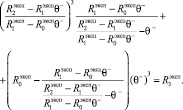 (10)
(10)
Очевидно, что для вычисления параметров 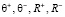 цифрового двойника по предварительно измеренным значениям
цифрового двойника по предварительно измеренным значениям 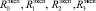 у человека нужно следовать следующему алгоритму:
у человека нужно следовать следующему алгоритму:
1. Решить уравнение (10) относительно коэффициента памяти θ–.
2. По формуле (8) вычислить значение θ+.
3. По формуле (9) вычислить значение параметра R+.
4. По формуле (7) вычислить значение отрицательной компоненты R– амбивалентного воспитания.
Для реализации этого алгоритма удобно использовать, например, широко известный программный пакет Mathematica [8].
Приведем результаты вычислений согласно предложенному алгоритму.
Пример 3
Для значений входных параметров воспитаний человека
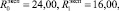
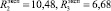 (11)
(11)
вычислены следующие значения параметров 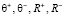 для его цифрового двойника:
для его цифрового двойника:
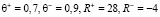 . (12)
. (12)
Таким образом, анализ результатов вычислений (12) позволяет сделать вывод, что для измеренных воспитаний (11) человек является злопамятным, а поэтому можно построить его злопамятный цифровой двойник. Отметим то, что злопамятность цифрового двойника определяется, прежде всего, справедливостью выполнения неравенства 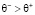 , и даже при выполнении соотношения
, и даже при выполнении соотношения 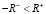 цифровой двойник является злопамятным.
цифровой двойник является злопамятным.
Расчеты показывают, что предложенный алгоритм не всегда позволяет определить злопамятность или незлопамятность человека и, как следствие, не всегда дает возможность построить злопамятного или незлопамятного цифрового двойника.
Приведем следующий пример.
Пример 4
Для численных значений входных параметров воспитаний человека
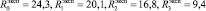
получены следующие значения параметров 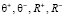 для его цифрового двойника:
для его цифрового двойника:
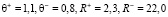 .
.
Легко видеть, что результаты вычислений не удовлетворяют допущениям предложенной математической модели, поэтому адекватность работы алгоритма необходимо определять по результатам вычислений, которые должны соответствовать условиям (2).
Заключение
Приведенные математические модели и алгоритмы вычисления параметров человека 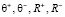 с последующим их использованием в качестве «психологических» характеристик цифрового двойника можно использовать при создании компьютерных игр, где их герои являются приближенными цифровыми аналогами конкретных людей.
с последующим их использованием в качестве «психологических» характеристик цифрового двойника можно использовать при создании компьютерных игр, где их герои являются приближенными цифровыми аналогами конкретных людей.
Библиографическая ссылка
Пенский О.Г., Анисимова С.И. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВЫЧИСЛЕНИЯ ПАРАМЕТРОВ ЗЛОПАМЯТНЫХ И НЕЗЛОПАМЯТНЫХ ЦИФРОВЫХ ДВОЙНИКОВ // Современные наукоемкие технологии. 2020. № 1. С. 17-20;URL: https://top-technologies.ru/ru/article/view?id=37896 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.37896



