CLEFIA – блочный алгоритм шифрования, в основе конструкции которого лежит структура Фейстеля. На вход данный алгоритм шифрования ожидает 128 бит, которые в дальнейшем разбиваются на 4 части по 32 бита. Алгоритм шифрования авторами позиционируется как легковесный, и в 2012 г. организации ISO и IEC включили алгоритм CLEFIA в международный стандарт облегчённого шифрования ISO/IEC 29192-2:2012 [1]. Одной из ключевых особенностей в проектировании данного алгоритма шифрования является использование так называемого Механизма переключения рассеивания (Diffusion Switching Mechanism – DSM), благодаря которому обеспечивается использование различный F-функций в разных раундах шифрования [2]. Механизм подразумевает чередование криптографических примитивов в виде блоков замены и матриц рассеивания. Согласно данному механизму, различается принцип использования математических F-функций. Для четных и нечетных F-функций различается порядок использования блоков замен S0 и S1, а также используются различные матрицы М0 и М1 для перемножения данных.
Цель работы: исследовать влияние механизма DSM на стойкость алгоритма Clefia.
Материалы и методы: алгоритм шифрования CLEFIA, метод дифференциального криптоанализа, ПЭВМ AMD Ryzen 5 1600 Six-Core Processor, язык программирования Python.
Алгоритм CLEFIA подразумевает использование четырех веток. Преобразование открытого текста может выполняться под воздействием секретного ключа длиной 128, 192 или 256 бит. В зависимости от этого преобразование будет выполняться в течение 18, 22 и 26 раундов соответственно. В данной статье анализировался шифр с четырьмя ветками и ключом, размером 128 бит. Через GFNd,r мы обозначим d-веточную и r-раундовую функцию используемую в CLEFIA.
Буквой T обозначим промежуточное значение, RKi – раундовый ключ, необходимый для вычислений, а X и Y тексты на входе и выходе соответственно. Тогда алгоритм GFNd,r можно расписать следующим образом:
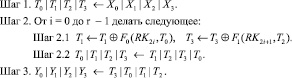
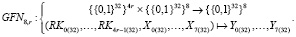
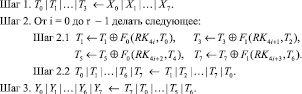
Обратная функция 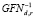 использует подключи RKi в обратном порядке, также меняется направление сдвигов на этапах 2.2 и 3.
использует подключи RKi в обратном порядке, также меняется направление сдвигов на этапах 2.2 и 3.
Алгоритм обработки данных CLEFIA можно представить функцией ENCr для зашифровки и DECr для расшифровки. Эти функции используют структуру GFN4,r, которая фактически представляет собой сеть Фейстеля с четырьмя ветками. Обозначим пару значений открытый текст – шифрованный текст как 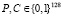 . Будем считать, что каждый текст может содержать 4 фрагмента
. Будем считать, что каждый текст может содержать 4 фрагмента 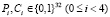 , где
, где 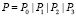 и
и 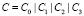 . Обозначим как
. Обозначим как 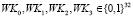 отбеливающие подключи и обозначим как
отбеливающие подключи и обозначим как 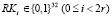 раундовые подключи. Функция DECr является обратной по отношению к функции ENCr, за счёт использования обратной функции
раундовые подключи. Функция DECr является обратной по отношению к функции ENCr, за счёт использования обратной функции 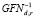 . На рис. 1 проилюстрирована функция ENCr.
. На рис. 1 проилюстрирована функция ENCr.
Алгоритм выработки раундовых подключей подразумевает различную реализацию для 128, 192 и 256 бит ключа. Так как в данной статье рассматривается версия алгоритм шифрования для секретного ключа размерностью 128 бит, то в дальнейшем будет рассмотрен алгоритм выработки раундовых подключей для 128-битного секретного ключа.
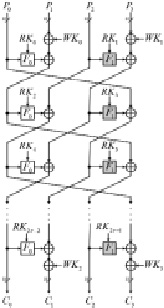
Рис. 1. Функция ENCr
Определим функцию DoubleSwap, используемую при выработке ключей, следую- щим образом:
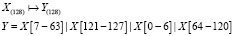 ,
,
где 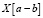 обозначает битовую строку, вырезанную начиная с бита a по бит b из строки X.
обозначает битовую строку, вырезанную начиная с бита a по бит b из строки X.
Алгоритм выработки раундовых подключей делится на две логические части: генерация промежуточного ключа L из исходного секретного ключа K и расширение K и L с целью генерации WKi и RKi. Промежуточный ключ L имеет длину 128 бит. Он генерируется с помощью функции 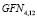 , на вход которой в качестве данных поступает значение секретного ключа
, на вход которой в качестве данных поступает значение секретного ключа 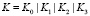 . При этом для преобразования в качестве раундовых подключей используется двадцать четыре 32-битных константы
. При этом для преобразования в качестве раундовых подключей используется двадцать четыре 32-битных константы 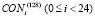 . Таким образом раундовые ключи K и промежуточный ключ L используются для генерации отбеливающих подключей
. Таким образом раундовые ключи K и промежуточный ключ L используются для генерации отбеливающих подключей 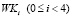 и раундовых подключей
и раундовых подключей 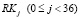 . На следующем шаге используется тридцать шесть 32-битных константных значений
. На следующем шаге используется тридцать шесть 32-битных константных значений 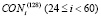 . Таким образом получается, что для генерации всех подключей требуется шестьдесят константных значений.
. Таким образом получается, что для генерации всех подключей требуется шестьдесят константных значений.
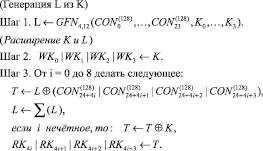
Функция F, используемая в процессе шифрования, имеет две реализации: F1 и F2. В самих функциях используются матрицы рассеивания, обозначаемые как M, и блоки замены, обозначаемые S. Работу каждой из F-функций можно описать следующим образом:
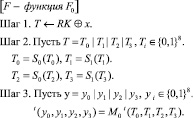
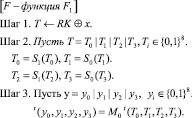
S0 и S1 представляют собой нелинейные 8-битные S-блоки. При этом в каждой из F-функций используется свой порядок применения S-блоков. Также разные F-функции используют на шаге 3 разные матрицы (М0 и М1). Матрицы имеют следующий вид (значения в матрице представлены в 16-ричном виде, a соответствует значению 10):
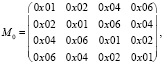
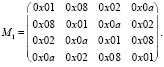
При этом полиномиальное перемноже- ние между матрицами и векторами производится в поле GF(28). В качестве нормализующего полинома используется полиномом z8 + z4 + z3 + z2 + 1. Структура для функций F0 и F1 приведена на рис. 2.
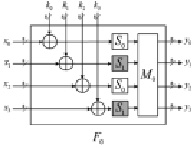
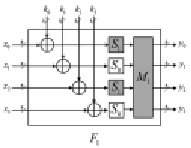
Рис. 2. Функции F0 и F1
Чередование матриц рассеивания и блоков замены, а также различные алгебраические структуры, лежащие в основе блоков замены, представляют собой Механизм переключения рассеивания. Изучение влияния данного Механизма переключения рассеивания на стойкость исследуемого алгоритма шифрования является одной из целей настоящего исследования.
В качестве метода исследования нами был выбран метод дифференциального криптоанализа, как один из наиболее популярных методов анализа симметричных блочных шифров [2]. Метод дифференциального криптоанализа рассматривает пары текстов при их изменении в зависимости от действий, совершаемых в каждом раунде. Впервые метод дифференциального криптоанализа был применен Э. Бихамом и А. Шамиром к анализу алгоритма шифрования DES [3, 4]. Сейчас этот метод широко применяется к анализу большинства шифров. В качестве дифференциала или разности рассматривается результат операции поразрядного сложения данных по модулю 2.
Матрицы рассеивания М0 и М1 размером 4х4 делят текст, поданный на вход, на 4 части по 8 бит, а далее эти 4 части подставляются в следующие уравнения:
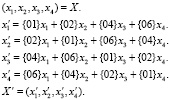
Все вычисления необходимо выполнять в поле GF(28) над многочленом z8 + z4 + z3 + z2 + 1, что подразумевает трактовку сложения как операцию побитового xor, а умножения – как перемножения двух полиномов по модулю z8 + z4 + z3 + z2 + 1 [5, 6]. Коэффициенты перед x представляют собой полиномы, которые выглядят следующим образом: 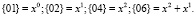
В первую очередь в ходе анализа была доказана обратимость матриц рассеивания по отношению к самим себе. Это позволяет нам легче находить удобную характеристику, если необходимо получить некоторую разность, которая дважды будет проходить через одну матрицу рассеивания. Следующим этапом было проанализировано поведение различных входов.
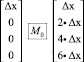
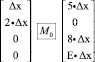
Учитывая обратимость матрицы самой себе, можно получить следующую закономерность: при 1 ненулевом входе, мы всегда будем получать 4 ненулевых выхода, подавая 2 ненулевых выхода, мы получим 3–4 ненулевых, при подаче 3 ненулевых мы можем получить на выходе от 2 до 4 ненулевых текстов и, подавая 4 ненулевых текста, на выходе получаем от 1 до 4 ненулевых текстов. Количество ненулевых выходов зависит от того, какие коэффициенты будут подобраны [5].
В ходе анализа блоков замены было выяснено, что блоки замены S0 представляют больший интерес в рамках дифференциального криптоанализа, так как вероятность преобразования одной разности в другую у данного блока замены может достичь более высоких вероятностей по сравнению с S1 [6]. Данный вывод легко сделать, обратив внимание на табл. 1.
Таблица 1
Таблица со статистикой преобразований в блоках замены
|
Вероятность |
n |
S0 |
S1 |
Вероятность |
n |
S0 |
S1 |
|
0 |
0 |
40022 |
33151 |
≈1/25,41 |
6 |
848 |
0 |
|
1/27 |
2 |
19501 |
32130 |
1/25 |
8 |
119 |
0 |
|
1/26 |
4 |
5037 |
255 |
≈1/24,68 |
10 |
9 |
0 |
Для анализа DSM механизма было необходимо ограничить область воздействия данного механизма или полностью его отключить. Отключение и ограничение подразумевают собой исключение разнообразия блоков замены и/или матриц рассеивания. Таким образом, к примеру, будут использоваться только S0, даже там, где должен был быть блок замены S1. То же касается матриц рассеивания.
Результаты исследования и их обсуждение
В ходе работы были проанализированы следующие вариации упрощений: шесть раундов без разнообразия M и S блоков, двенадцать раундов без разнообразия M и S блоков, двенадцать раундов без разнообразия M блоков, шесть раундов с DSM механизмом и девять раундов с DSM механизмом. Вариации с шестью раундами использовались не столько для получения сложности нахождения дифференциальной характеристики, сколько для того, чтобы убедиться в правильности найденных характеристик с помощью персонального компьютера. Таким образом шестираундовые характеристики были вручную найдены на персональном компьютере, в то время как остальные были разработаны теоретически. Перебор и вычисления осуществлялись с помощью ПЭВМ со следующими характеристиками: процессор AMD Ryzen 5 1600 Six-Core Processor.
Для проведения полного анализа механизма DSM были проведены эксперименты для различных вариантов использования блоков замены и матриц М0 и М1. были по очереди отключены разнообразия блоков замены и матриц М. В ходе работы были разработаны алгоритмы анализа с учетом различных вариантов упрощений шифра. Кроме того, чтобы иметь возможность оценить влияние DSM-механизма в полной мере, были построены дифференциальные характеристики для различного числа раундов шифрования (от 6 до 12) и для них теоретически просчитаны значения вероятностей. Результаты теоретических рассчетов и практических экспериментальных данных сведены в табл. 2. В каждом эксперименте было атаковано 8 бит ключа.
Таблица 2
Сложность анализа в зависимости от конфигурации алгоритма
|
Раунды |
S |
М |
Реализация |
Итоговая сложность |
|
6 |
только S0 |
только М0 |
практическая |
1/214,04 |
|
6 |
S0 и S1 |
М0 и М1 |
практическая |
1/216,36 |
|
9 |
S0 и S1 |
М0 и М1 |
теоретическая |
1/2125,39 |
|
12 |
только S0 |
только М0 |
теоретическая |
1/294,7 |
|
12 |
S0 и S1 |
только М0 |
теоретическая |
1/295 |
Можно видеть, что при использовании только одной матрицы М0 в DSM-механизме, сложность анализа 12 раундов будет ниже сложности анализа 9 раундов, где используются обе матрицы М0 и М1. Это связано с тем, что в случае с двумя матрицами М0 и М1, чем больше раундов, тем тяжелее подобрать удобные разности для построения итогового дифференциала. В ходе анализа было показано, что при использовании обеих матриц М0 и М1 невозможно получить одинаковые выходы разностей при использовании одинаковых разностей на входах в F-функцию. Одним из приемов, который часто используется в дифференциальном криптоанализе, является пропуск некоторых преобразований, где на вход поступает разность, равная нулю. В данном же случае, при использовании разных матриц М0 и М1, выявленное свойство не позволяет пропускать преобразования и вероятность начинает уменьшаться слишком быстро. При использовании в каждой F-функции одинаковых матриц в результате анализа удалось построить характеристику для 12 раундов шифрования. Вероятность появления такой характеристики составила 1/294,7. В то же время при использовании разных матриц М0 и М1 удалось построить характеристику только для 9 раундов. При этом вероятность появления такой характеристики оказалась слишком маленькой 1/2125,39, что слишком близко к полному перебору.
Аналогичный эксперимент проводился и для чередования S-блоков замены. Было показано, что для блока S0 в таблице присутствуют более высокие значения вероятностей, чем для блока S1. Также было показано, что для блоков S0 и S1 одинаковые значения входных разностей очень часто не могут быть преобразованы к одинаковым значениям разностей на выходе, что сильно затрудняет построение многораундовых характеристик.
Заключение
В результате проделанной работы было показано, что использование DSM-механизма в составе алгоритма шифрования CLEFIA не случайно, а имеет обоснованные причины использования. Наличие DSM-механизма значительно увеличивает сложность анализа шифра. Как следствие, при рассмотрении варианта шифра с использованием DSM-механизма можно проанализировать гораздо меньше раундов шифрования, чем при рассмотрении шифра без DSM-механизма.
Работа выполнена при поддержке гранта РФФИ № 17-07-00654 «Разработка и исследование последовательных и параллельных алгоритмов анализа современных симметричных шифров с использованием технологий MPI, NVIDIA CUDA, SageMath».
Библиографическая ссылка
Ищукова Е.А., Куликов А.В. ИССЛЕДОВАНИЕ АЛГОРИТМОВ АНАЛИЗА ШИФРА CLEFIA // Современные наукоемкие технологии. 2019. № 12-2. С. 287-292;URL: https://top-technologies.ru/ru/article/view?id=37873 (дата обращения: 26.02.2026).
DOI: https://doi.org/10.17513/snt.37873



