Шагающие роботы относятся к интенсивно развивающемуся классу роботов. Активно развивающимся направлением являются инсектоморфные роботы, которые обладают повышенной устойчивостью по сравнению с антропоморфными [1–2] или зооморфными роботами [3] за счет большего количества ног. Такие многоногие роботы малых размеров могут быть изготовлены с использованием 3D-принтера [4].
Шагающие роботы обладают высокой способностью по преодолению препятствий, но движение по ровной поверхности неэффективно из-за высоких энергозатрат, особенно для инсектоморфных роботов. Повышение энергоэффективности и скорости передвижения шагающих роботов является актуальным направлением исследований. Исследователями предлагаются разные пути решения проблемы, например введение новых режимов передвижения робота путем изменения его кинематической схемы. Одним из направлений является совмещение колесного и шагового перемещений, например, у робота-паука компании Festo [5]. В данной работе рассматривается использование дополнительного одноколесного движителя для увеличения мобильности и энергоэффективности робота при движении по ровной поверхности.
Ставится задача синтеза управления шагающим роботом в двух режимах – режиме движения только на шагающих движителях и режиме движения с помощью одноколесного движителя с балансированием и подруливанием частью шагающих движителей. В результате решения такой задачи получены кинематические параметры програм- мных движений приводов шагающих движителей в указанных двух режимах.
Материалы и методы исследования
Решается обратная задача динамики, с использованием программного комплекса моделирования динамики связанных систем тел ФРУНД (http://frund.vstu.ru) [6, 7]. Особенностью данного подхода является точный учет кинематической схемы робота в расчетной схеме, в отличие от общепринятых методов редукции, приводящих к упрощенным уравнениям с 1–2 степенями свободы. Такой подход особенно важен для синтеза программного движения подруливающих движителей в режиме движения с использованием одноколесного движителя.
Синтез управляемого движения
Разработан метод синтеза программного движения шагающих роботов методом обратной задачи. Метод использует точные выражения статических слагаемых уравнений координат точки нулевого момента, определяющей устойчивость походки. Общее уравнение динамики движения робота как пространственной механической системы можно записать в виде
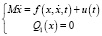 . (1)
. (1)
Здесь x – вектор координат всей системы размерностью n×6, где n – число тел системы, M – матрица инерции, 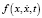 – вектор позиционных, диссипативных и внешних сил, Q1(x) – вектор уравнений связей размерностью k1, описывающих кинематические пары, u(t) – матрица сил (моментов) в приводах, приведенная к координатам тел.
– вектор позиционных, диссипативных и внешних сил, Q1(x) – вектор уравнений связей размерностью k1, описывающих кинематические пары, u(t) – матрица сил (моментов) в приводах, приведенная к координатам тел.
Уравнения (1) принято называть уравнениями прямой задачи. В терминах аналитической механики уравнения (1) описывают систему с голономными связями. Для нахождения управлений u(t) в методе обратной задачи действия управляющих сил заменяются дополнительными уравнениями связей. Уравнения (1) применительно к шагающим роботам в этом случае приобретают вид
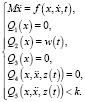
Уравнение (2в) размерностью k2 задает кинематику движения опорных точек робота и его корпуса. Вектор функция w(t) включает в себя траектории точек ног и корпуса. Уравнение (2г) размерностью k3 задает вспомогательные связи для исключения избыточных степеней свободы всего робота. Уравнение (2д) размерностью k4 ≤ 3 определяет выполнение условий устойчивости. Скалярное неравенство (2е) задает условие отсутствия скольжения в опорных точках робота, которое зависит от коэффициента трения об опорную поверхность k.
Два последних уравнения являются уравнениями для условий устойчивости, и на настоящий момент не разработано методов точного численного решения (2) с учетом связей такого типа, содержащих вторые производные от координат системы. В существующих работах [8–10], как правило, учитывается только уравнение (2д) в упрощенном виде. В настоящей работе из уравнения (2д) исключаются члены со вторыми производными. При численном решении уравнений (1–2) используется общепринятый показатель точности – максимальная погрешность уравнений связей, которая принималась равной 10-6 м.
Движение робота по ровной поверхности и по макропрепятствиям с помощью шагающих движителей
В данный момент разработаны теоретические методы и программное обеспечение, позволяющие синтезировать управление движением роботов с произвольным количеством ног – двуногих, шестиногих, многоногих.
Эти роботы могут совершать произвольные движения, например подъем по лестнице (рис. 1). Формирование управления для такого типа движения выполнено за счет соответствующих функций w(t), которые задают пространственное движение стоп и корпуса. Преодоление лестничных пролетов является важной задачей для мобильных роботов, решение которой для роботов с традиционными движителями, например гусеничным, требует значительного увеличения габаритов робота. Использование шагающих движителей позволяет добиться требуемого функционала роботами относительно небольшого размера.
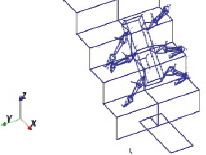
Рис. 1. Преодоление роботом ступеней
Относительные размеры робота, позволяющие выполнять такой вид движения, при высоте ступени 20 см приведены в таблице. Длина робота в таком случае составляет около 60 см, ширина – около 40 см. Суммарная длина ног 40 см. То есть габариты робота будут относительно небольшими.
Размеры робота для преодоления ступеней
|
Параметр |
Значение, см |
|
длина ног |
40 (7 + 14 + 19, БЕДРО, ГОЛЕНЬ, СТОПА) |
|
расстояние между ногами продольное |
20 |
|
расстояние между ногами поперечное |
26 |
Движение робота с помощью одноколесного движителя
Основными недостатками роботов с шагающими движителями являются малая скорость передвижения и низкая энергоэффективность, особенно для шагающих движителей инсектоморфного типа. Указанные показатели можно значительно улучшить путем введения дополнительного колесного движителя.
По предложенной кинематической схеме была создана математическая модель многоногого робота в программном комплексе ФРУНД, приведенная на рис. 2.
(2а)
(2б)
(2в)
(2г)
(2д)
(2е)
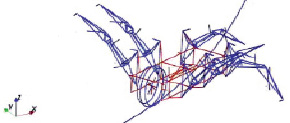
Рис. 2. Модель робота с колесным движителем
Такая структура позволяет объединить преимущества шагающего робота, такие как высокая профильная проходимость – преодоление ступенек и других единичных препятствий, с достоинствами колесных роботов – высокой скоростью передвижения и высокой энергоэффективностью.
Обладая дополнительным колесным движителем, инсектоморфный робот может быстро преодолевать большие открытые пространства с относительно ровной поверхностью, сохраняя при этом энергию, необходимую для преодоления труднопроходимой местности.
При наличии препятствий или сложном профиле поверхности робот выполняет шаговое перемещение, как обычный инсектоморфный робот. Если надо переместиться по ровной поверхности, то робот поднимает передние ноги, опираясь на колесо, и движется по заданной траектории, подруливая задними ногами (рис. 3). Алгоритм подруливания использует рассогласование между направлением вектора скорости характерной точки робота и касательной к заданной программной траектории. Само подруливание выполняется одной парой ног – рис. 3 и реализуется за счет поперечного смещения концевых точек стоп указанной пары ног пропорционально рассогласованию вектора скорости и касательной к траектории. В расчетах принималось, что на подруливающую пару ног приходилось 20 % общего веса робота. Результаты моделирования представлены на рис. 3. Максимальная погрешность отклонения ц.м. корпуса от программной траектории составляла 0.1 м, что, на наш взгляд, достаточно для транспортного режима перемещения робота.

Рис. 3. Подруливание при перемещении по траектории
Рабочие режимы движения робота
Важным достоинством многоногого робота является возможность работы в режиме манипулятора (рис. 4). При работе в данном режиме робот выполняет заданное программное движение определенной точки за счет шагающих движителей.

Рис. 4. Многоногий робот с манипулятором
Использование шагающих движителей в режиме манипулятора, с одной стороны, упрощает конструкцию робота как манипулятора, поскольку или не требует введения дополнительных управляемых степеней свободы в конструкцию робота, или допускает добавление ограниченного числа таких степеней свободы. При этом в обоих случаях обеспечивается пространственный характер движения концевого звена манипулятора, в том числе как по поступательным степеням свободы, так и по вращательным. Такой манипулятор по общепринятой классификации относится к 6D манипуляторам. Работа в режиме манипулирования может так же разделяться на два режима.
В первом режиме движение концевой точки осуществляется без перешагивания шагающих движителей. В этом случае величина рабочей зоны ограничивается размерами звеньев шагающих движителей, так как стопы движителей остаются неподвижными относительно опорных поверхностей. Манипулятор в таком режиме работы обладает повышенной жесткостью, поскольку является по существу параллельным механизмом с шестью параллельными силовыми контурами (для рассматриваемого варианта робота). Наличие шести контуров приводов также увеличивает точность позиционирования, и кроме этого, для достижения заданных силовых характеристик манипулятора требуются приводы меньшей мощности.
Во втором режиме движение концевой точки осуществляется с перешагиванием шагающих движителей. В этом случае величина рабочей зоны в горизонтальной плоскости ничем не ограничивается. В вертикальном направлении рабочая зона может быть увеличена, например, за счет добавления звена с одной степенью свободы относительно корпуса робота.
Добавление режима манипулятора позволяет использовать мобильного робота для выполнения различных задач, предлагаемых шагающим роботам, таких как, например, сбор проб, открытие вентилей, перемещение грузов или разминирование объектов.
Заключение
Малоразмерный шагающий робот с колесным движителем является удобной платформой для создания высокомобильных сервисных роботов различного назначения – осмотр внутренних помещений, сбор проб и т.д. Его преимуществами являются:
– низкая стоимость и простота изготовления механической части;
– высокая унификация аппаратной части системы управления;
– модульность конструкции.
Перспективным направлением исследований является использование малоразмерных шагающих роботов с колесным движителем для отработки программной части систем управления с элементами искусственного интеллекта в реальных эксплуатационных условиях.
Созданные методы управления локомоцией шагающих роботов могут быть использованы для роботов с различными типами шагающих движителей. Для роботов большой размерности и грузоподъемности могут применяться движители на основе дельтаподобных механизмов.
Библиографическая ссылка
Горобцов А.С., Чигиринская Н.В., Андреева М.И., Смирнов Е.А., Бочкин А.М. ИССЛЕДОВАНИЕ УПРАВЛЯЕМОГО ДВИЖЕНИЯ ШАГАЮЩИХ РОБОТОВ МЕТОДАМИ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ ДИНАМИКИ СВЯЗАННЫХ СИСТЕМ ТЕЛ // Современные наукоемкие технологии. 2019. № 12-2. С. 282-286;URL: https://top-technologies.ru/ru/article/view?id=37872 (дата обращения: 31.01.2026).
DOI: https://doi.org/10.17513/snt.37872



