Технологические требования к равномерности движения приводов существенно ужесточаются в условиях, при которых исполнительный электропривод должен обеспечивать исключительно широкий диапазон регулирования параметров выполнения технологических операций.
При движении в системе электропривода могут возникать повышенные ускорения и динамические моменты. Люфты и зазоры в механических передачах приводов в сильной степени влияют на характер движения исполнительных систем. Широкий спектр неравномерности скорости привода может при совпадении частот привести к возникновению механических колебаний значительной амплитуды. Все это увеличивает износ деталей и узлов механизмов, снижает их механическую надежность, может привести к поломкам и выходу из строя, что совершенно недопустимо. Эти же причины могут потребовать введения либо дополнительного механического демпфирования, либо упругих компенсаторов. Это приведет к снижению чувствительности по перемещению или ухудшению динамических качеств привода. Конструктивные требования к равномерности движения привода становятся важными, учитывая тенденции непосредственного соединения вала исполнительного двигателя с ходовым винтом, исключая промежуточный редуктор, который способен во многом снизить уровень неравномерности движения конечного звена привода. Становится важной задача компенсации упругих свойств механических передач, влияющих на процесс выполнения технологических операций при силовом взаимодействии. Рост статического момента нагрузки приводит к увеличению перерегулирования в переходных режимах и снижению запаса устойчивости системы. Аналогичное влияние оказывает изменение момента инерции нагрузки. При гармонических входных сигналах увеличение их частоты вызывает снижение точности, установившаяся динамическая ошибка недопустимо возрастает.
Для обеспечения равномерности движения широко используется адаптивное управление. Применению адаптивного управления посвящено немало работ Я.З. Цыпкина, А.А. Воронова, Р. Изермана, А.В. Тимофеева и др. Однако введение дополнительного контура в структуру привода усложняет систему управления, может приводить к неустойчивости процесса управления, сложно в настройке.
Еще одним принципом управления для компенсации возмущений является скользящий режим работы в системах с переменной структурой. Наиболее полно возможности скользящих движений были выявлены и использованы в работах по теории систем с переменной структурой, которые в настоящее время сформировались в самостоятельное научное направление в общей теории нелинейных систем [1].
Процессы носят случайный характер, и описать их аналитически довольно сложно, а реализация классическими методами затруднительна. В связи с этим для решений обозначенных задач предлагается использовать алгоритмы управления, основанные на нечеткой логике.
Основанием для такого решения является доказательство Вангом в 1992 г. теоремы о существовании нечеткой системы, формирующей выходную функцию, такую, что верхняя граница разности исходной функции и выходной меньше или равна некоторой произвольной постоянной. В 1993 г. Б. Коско доказал FAT теорему (Fuzzy Approximation Theorem), в которой говорится о том, что любая математическая система может быть аппроксимирована системой на основе нечеткой логики. И, наконец, в 1995 г. Кастро показал, что логический контроллер Мамдани при определенных условиях является универсальным аппроксиматором. Эти работы послужили активному применению нечеткой логики в различных отраслях знаний, в том числе и в системах автоматического управления [2–4].
Таким образом, использование нечеткого контроллера (НК) в структуре системы автоматического управления (САУ) позволит решить задачу компенсации возмущений с минимальной ошибкой более простыми и эффективными методами.
Цель исследования: разработка метода обеспечения равномерного движения компенсацией параметрических возмущений, возникающих в приводе, и недетерминированных возмущений гармонического характера, вызванных технологическим процессом. Компенсация возмущений рассматривается на примере привода электромеханической системы робота, в которой возмущения в силу конструктивных решений не могут быть измерены.
Материалы и методы исследования
В качестве объекта исследования рассматривается привод перемещения с главной обратной связью по положению. Объект управления имеет конечную жесткость и коэффициент демпфирования, а отсутствие информации о возмущающем воздействии затрудняет обеспечение заданных показателей работы САУ.
Рассматриваемая далее САУ представляет собой систему с переменной структурой (СПС). Характерным видом движения в таких системах являются скользящие режимы, важной особенностью которых является состояние при котором, попав на линию переключения, дальнейшее движение в системе будет осуществляться вдоль этой линии, являющейся линией переключения, и никогда с нее не сойдет при любом возмущении [1, 5]. Кроме того, скользящий режим в рассматриваемом случае определяется не параметрами объекта, а параметрами созданного подпространства скольжения.
С точки зрения обработки нечеткостей нельзя получить результаты, пока не будут исследованы в полной мере исходные данные, оценена общая структура проблемы, исключены сомнительные данные.
Для систем автоматического управления нет практических рекомендаций к выбору функций активации, их числа, мощности множеств, диапазонов, что сильно осложняет процесс построения приводов с нечетким контроллером в структуре.
САУ с таким видом движения реализуем на основе НК, выполняющего роль регулятора, формирующего управление на основе измерения положения и угловой скорости.
Структурная схема, реализующая данный подход, представлена на рис. 1.
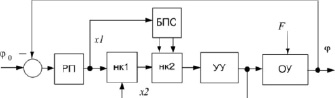
Рис. 1. Структурная схема электропривода переменной структуры с нечетким регулятором: НК1 – нечеткий контроллер вычисления S, НК2 – нечеткий контроллер переключения структур РП – регулятор положения, БПС – блок переключаемых структур, УУ – управляющее устройство, ОУ – объект управления, F – возмущение, φ – угловое положение
Она представляет собой электропривод с нечетким СПС регулятором. Основными устройствами в схеме являются два нечетких контроллера включенных последовательно НК1 и НК2. НК1 выполняет функции вычисление кривой скольжения, а второй НК, в зависимости от знака произведения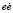 
вычисленного в НК1 обеспечивает переключение структур реализованных в блоке переключаемых структур БПС. Входным сигналом на БПС является сигнал с выхода регулятора положения. Этот сигнал используется и в НК1. Устройство управления УУ может быть любым, обеспечивающим угловое перемещение φ исполнительного механизма. Выходной сигнал с УУ используется НК1. Объект управления при возникающих возмущениях F перемещается не равномерно. В качестве входного воздействия φ0 используются типовые входные воздействия.
Алгоритм работы схемы следующий. На универсальном множестве P, характеризующем пространство состояний САУ, имеем два подмножества:
– подмножество S, характеризуемое функцией принадлежности μS(x1). Подмножество S множества P есть множество пар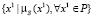 
описывающих сигнал регулятора положения;
– подмножество V, характеризуемое функцией принадлежности μV(x2). Подмножество V множества P есть множество пар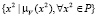 
описывающих скорость вращения ротора двигателя.
В качестве функций принадлежности используем Z функцию, которая задается аналитическим выражением
fZ (x; a, b) =
= 
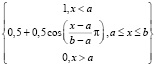(1)
и S функцию, для которой аналитическое выражение аналогично
fS (x; a, b) =
= 
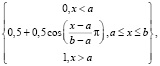(2)
где а, b – числовые параметры, принимающие действительные значения и упорядоченные отношением: а < b.
Разница в том, что рассматриваемые функции принадлежности порождают нормальные выпуклые нечеткие множества с ядром (–∞, а) и носителем (–∞, b) для Z функции и с ядром (b, +∞) и носителем (а, +∞) для S функции.
Чем меньше уверенность в точности измерения, тем большим будет интервал носителя соответствующего нечеткого множества. Именно по этой причине фаззификация позволяет более адекватно представить объективно присутствующую неточность результатов физических измерений. Это хорошо согласуется с принципом управления, когда любое отклонение от кривой скольжения вызывает соответствующую реакцию для переключения структуры. Входные терм множества определялись по результатам анализа фактических данных [6, 7]: диапазон ошибки регулятора положения, значение скорости, величина отклонения от траектории движения.
Для обеспечения движения необходимо добиться выполнения условия, при котором произведение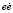 
< 0, где e является линией переключения (скольжения), а 
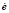ее производная.
Это решает НК1. Его выходное множество также имеет сплайн-функции принадлежности, характеризующие величину отклонения от реализуемой траектории движения. В соответствии с принципом управления уравнение скольжения запишется в следующем виде e = CmS(x1) + mV(x2).
База знаний НК1 представлена двумя правилами, так как в соответствии с принципом работы необходимо оценивать знак е. Оценка осуществлялась с использованием конструкции Мамдани. Изначально находим a – уровни для каждого из правил с использованием операции min: a1 = S1(x1)∧V1(x2), a2 = S2(x1)∧V2(x2) а затем соответствующие им функции принадлежности: m1(e) = a1∧K1(e), m2(e) = a2∧K2(e).
Вывод выполним с использованием операции MAX, производя объединение усеченных функций. В результате получаем переменную выхода с функцией принадлежности: mS(e) = (a1∧K1(e))∨(a2∧K2(e)).
Изменение структуры реализуется с помощью НК2. Входная функция представлена функциями вида (1) и (2). Имеет два терма «Больше» и «Меньше». Выходная переменная представлена трапецеидальными функциями.
Закон изменения структуры основан на анализе произведения emS(x1)
Y =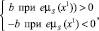 
а управляющее воздействие: u = ΨμS(x1).
Вывод реализуется аналогичным образом, как и для НК1.
В [1] отмечено, что если функция управления формируется из регулируемой величины и ее производных, то движение в скользящем режиме не зависит от параметров объекта и внешних возмущений. В рамках одной линейной структуры для стабилизации необходимо в управление добавить воздействие по х2 – производной от координаты х1. Таким образом, в результате изменения структуры удается парировать внешнее возмущение, которое недоступно для измерения, и сделать величину ошибки после окончания процесса управления равной нулю [5].
Результаты исследования и их обсуждение
Исследование работоспособности рассматриваемой структуры автоматического управления было реализовано в пакетах Simulink и Fuzzy Logic Toolbox программы MatLab на примере электропривода постоянного тока, расположенного в суставе робототехнической системы. Полагалось, что ОУ подвержен влиянию внешнего неизмеряемого возмущения, имеющего вид гармонической функции. Исследования проводились для оценки работоспособности и характеристик нечеткой следящей системы; инвариантности к изменению собственных параметров и способности системы к компенсации внешних возмущений.
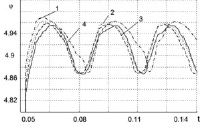
Анализ влияния возмущений оценивался при изменении амплитуды и частоты возмущений. Амплитуда возмущений изменялась в интервале от 0,5 до 2 и фиксировался процесс движения следящей системы (рис. 2, а). Рассматривался установившийся режим движения при скачкообразном входном воздействии.
а) б)
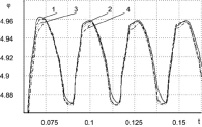
Рис. 2. Влияние амплитуды а) и частоты б) возмущения на выходную координату: а) изменение амплитуды при постоянной частоте возмущений: F4 = 0, F3,2,1 = (0,5…2)Sin(2t + 1,57), б) изменение частоты возмущений при постоянной амплитуде: 1 – F = 2Sin(2t + 1,57), 2 – F = 2Sin(3t + 1,57), 3 – F = 2Sin(4t + 1,57), 4 – F = 2Sin(5t + 1,57)
Изменение амплитуды возмущений составляло 50 % от входного задания, что для реальных систем вряд ли целесообразно, так как приводные системы не проектируются по моменту нагрузки до величин вдвое превосходящие допустимые.
Изменение частоты возмущающего воздействия в моделируемых ситуациях компенсируется и практически не влияет на характер движения системы (рис. 2, б).
Таким образом, рассматриваемая САУ компенсирует неизмеряемое возмущение по частоте и амплитуде с незначительным отклонением по сравнению с невозмущенным движением и в первую очередь за счет принципа действия систем с переменной структурой.
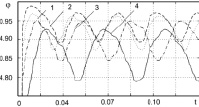
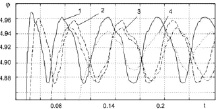
Изменение коэффициента усиления регулятора положения в диапазоне от 14,7 до 30,2 приведено на рис. 3, а. С ростом коэффициента усиления уменьшается амплитуда отклонения от кривой и возрастает частота переключения структур. При этом увеличивается и рассогласование между заданным входным сигналом и сигналом по цепи обратной связи примерно на 2 %. Для компенсации этого явления необходима коррекция параметров цепи обратной связи. Следует заметить, что изменение коэффициента усиления в два раза на практике маловероятно.
а) б)
Рис. 3. Влияние коэффициента усиления регулятора положения а) и управляющего устройства б): а) 1 – Крп = 20,0; 2 – Крп = 14,7; 3 – Крп = 25; 4- Крп= 30,2; б) 1 – Коу = 40,2; 2 – Коу=20,2; 3 – Коу = 25,2; 4 – Коу = 35.
Аналогичное изменение параметров управляющего устройства приводит с уменьшением коэффициента усиления к увеличению времени переходного процесса и в незначительном изменении частоты переключения структур (рис. 3, б). Изменение параметров САУ не оказывает существенного влияния на выходные характеристики.
Заключение
Исследование модели показало принципиальную возможность построения приводов с переменной структурой в классе систем, использующих нечеткую логику. Рассмотренная система работоспособна, характеристики нечеткой системы показывают инвариантность к изменению собственных параметров и способность к компенсации внешних возмущений. Структура привода с НК реализуется значительно проще. База знаний имеет всего лишь четыре записи, обеспечивающие желаемые выходные характеристики. Единственный недостаток связан с конечной частотой переключений, в силу чего в выходном сигнале появляется периодическое отклонение незначительной величины.
Отсутствие методик построения приводов с НК требует более широких исследований по реализации структур и формирования баз знаний. Необходима новая парадигма в создании САУ с искусственным интеллектом.
Простая замена известных средств реализации систем на методы искусственного интеллекта позволяет реализовать систему с желаемыми характеристиками более просто.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-08-01126.
Библиографическая ссылка
Веселов О.В., Светушенко С.Г. НЕЧЕТКИЙ КОНТРОЛЛЕР КОМПЕНСАЦИИ НЕИЗМЕРЯЕМЫХ ВОЗМУЩЕНИЙ В ПРИВОДАХ ИСПОЛНИТЕЛЬНЫХ СИСТЕМ // Современные наукоемкие технологии. – 2019. – № 12-2. – С. 271-275;URL: https://top-technologies.ru/ru/article/view?id=37870 (дата обращения: 19.04.2024).