Электроимпедансная томография (ЭИТ) – неинвазивный метод реконструкции и визуализации распределения поля электрической проводимости внутренних структур биологических объектов по результатам электрических измерений на его поверхности [1–3]. В общем случае, практическая реализация метода ЭИТ заключается в подключении исследуемого объекта (ИО) к одному или нескольким источникам электрического тока высокой частоты и малой амплитуды через электроды, размещенные на его поверхности, и регистрации потенциалов φ(i, j) в точках крепления электродов (где i – номер пары инжектирующих электродов, j – номер измерительного электрода) [1]. Используемые в ЭИТ алгоритмы реконструкции используют математическую модель объекта исследования, расчёт сопротивления объекта осуществляется путём решения дифференциальных уравнений для каждого среза [2]. Одним из перспективных направлений ЭИТ является трехмерная ЭИТ, позволяющая получать информацию о параметрах поля проводимости внутренних структур ИО как в отдельном двухмерном томографическом срезе, так и в их совокупности [3]. Использование нескольких электродных поясов пациента позволяет формировать томографические срезы не только в плоскости электродных поясов, но и в других проекциях, предлагая новую функциональность в виде многоракурсности.
Цель исследования: реализация многоракурсной ЭИТ (МРЭИТ) в аппаратно-программных комплексах создает ряд проблем, одной из которых является ресурсоемкость процесса реконструкции.
Для определения параметров ресурсоемкости процесса дифференциальной реконструкции [2] (использованного объёма оперативной памяти (ОЗУ) электронно-вычислительной машины (ЭВМ) Vср, общего затраченного времени tобщ, времени формирования кадра tуд, частоты кадров в секунду k) проведено исследование, в котором использовано минимальное для дифференциальной реконструкции количество входных файлов n = 2, общее количество файлов N = 4260.
В качестве объекта исследования выбран фантом с цилиндрическими неоднородностями заданного размера [4]. Параметры ЭВМ, используемой для проведения исследования: размер установленного ОЗУ ЭВМ – 6 Гб, тактовая частота процессора ЭВМ – 3,20 ГГц, версия операционной системы (ОС) – Windows 8.
В результате проведенного исследования были получены следующие показатели ресурсозатратности: Vср – 410,80 Мб, tобщ – 513,30 с, tуд – 0,85 с, k – 1,16 кадров/с. Таким образом, выявлено, что при реконструкции поля проводимостей методом ЭИТ возникает проблема низкой скорости визуализации результатов реконструкции, не позволяющей при полученной k отслеживать динамику некоторых физиологических процессов (например, воздухонаполнение легких, сердцебиение).
Одним из путей решения данной проблемы является определение такого числа n, которое может обработать программный пакет за один вызов процесса реконструкции без превышения Vср. В связи с этим предложен для разработки алгоритм выбора необходимого количества n в зависимости от конфигурации используемого в составе аппаратно-программного комплекса персонального компьютера, заключающийся в тестировании компонентов программного обеспечения (ПО) для определения параметров обработки входных файлов для процесса реконструкции при используемой в задачах МРЭИТ конфигурации персонального компьютера.
Материалы и методы исследования
Алгоритм реализован с помощью языка программирования Python [5]. Исследование разработанного алгоритма выполнено на АПК ЭИТ БО [6–8]. Процесс реконструкции и визуализации проводился с помощью программного пакета EIDORS [9]. Проведено исследование на двух ЭВМ, № 1 и № 2, с параметрами, приведенными на табл. 1, целью исследования являлось определение Vср для процесса реконструкции одного томографического среза при МРЭИТ.
Таблица 1
Параметры исследуемых ЭВМ
|
Версия операционной системы (ОС) |
Размер ОЗУ |
Тактовая частота процессора |
|
|
№ 1 |
Windows 8 |
8 ГБ |
3,5 ГЦ |
|
№ 2 |
Windows 8 |
6 ГБ |
3,2 ГЦ |
Блок-схема обобщенного алгоритма исследования Vср приведена на рис. 1. Алгоритм работы программы, разработанной для проведения данного исследования, состоит в следующем: программой осуществляется прием заданного количества входных файлов n для процесса реконструкции, поэтапно обрабатываются все входные файлы N = 4260. После завершения процесса работы EIDORS в параметрах программы АПК ЭИТ БО задается новое значение n и регистрируются параметры Vср, tобщ, tуд и k для нового процесса реконструкции.
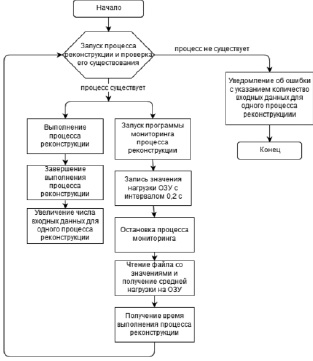
Рис. 1. Блок-схема обобщенного алгоритма исследования Vср , tуд , tобщ , k
Таблица 2
Исследование зависимости Vср, tуд, tобщ, k от n для ЭВМ № 1
|
N |
n |
Vср, Мб |
tуд, с |
tобщ, с |
k, кадров/с |
|
4260 |
10 |
563,5 |
0,330 |
1283,70 |
3,3 |
|
4260 |
71 |
129,8 |
0,090 |
412,60 |
10,3 |
|
4260 |
355 |
84,8 |
0,083 |
354,70 |
12,0 |
|
4260 |
2130 |
83,5 |
0,081 |
346,80 |
12,3 |
|
4260 |
4260 |
– |
– |
– |
– |
Таблица 3
Исследование зависимости Vср, tуд, tобщ, k от n для ЭВМ № 2
|
N |
n |
Vср, Мб |
tуд, с |
tобщ, с |
k, кадров/с |
|
4260 |
10 |
549,9 |
3,77 |
16099,5 |
0,20 |
|
4260 |
71 |
125,6 |
0,45 |
1915,6 |
2,22 |
|
4260 |
355 |
81,4 |
0,31 |
1326,9 |
3,21 |
|
4260 |
2130 |
80,3 |
0,26 |
1121,3 |
3,79 |
|
4260 |
4260 |
– |
– |
– |
– |
Результаты исследования зависимости Vср, от n приведены на табл. 2 и 3.
Анализ полученных результатов показывает, что при увеличении n для процесса реконструкции уменьшается Vср и снижается время выполнения работы ПО EIDORS. При увеличении n до N зарегистрировано превышение объема выделяемой ОЗУ и завершение процесса реконструкции системной ошибкой. На рис. 2 и 3 приведены зависимости изменения Vср, tуд процесса реконструкции одного файла от n для ЭВМ № 1 и ЭВМ № 2.
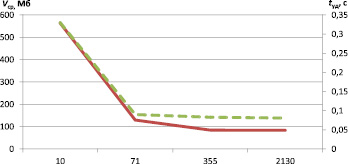
Рис. 2. Зависимость Vср , tуд от n для ЭВМ № 1 в составе АПК ЭИТ БО
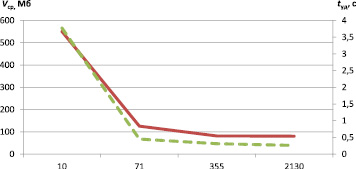
Рис. 3. Зависимость Vср , tуд от n для ЭВМ № 2 в составе АПК ЭИТ БО
Сплошной линией обозначен график потребления Vср процессом реконструкции, пунктирной линией обозначены связанные с его выполнением временные затраты tуд. Анализ рис. 2 и 3 показывает, что значение показателей Vср и tуд процесса реконструкции уменьшается до достижения значения n = 71 (1,66 % от общего числа файлов), дальнейшее увеличение параметра n не приводит к значительному росту скорости обработки входных данных.
Для определения n для каждого процесса реконструкции, при котором ресурсоемкость его минимальна, разработан алгоритм, основанный на методе бинарного поиска.
Бинарный (двоичный) поиск – это поиск заданного элемента на упорядоченном множестве, осуществляемый путем неоднократного деления этого множества на две части таким образом, что искомый элемент попадает в одну из этих частей. Поиск заканчивается при совпадении искомого элемента с элементом, который является границей между частями множества или при отсутствии искомого элемента [10].
Разработанный алгоритм позволяет определить максимальное n для одного процесса реконструкции без превышения Vср. Данный алгоритм реализован на языке программирования Python. Блок-схема алгоритма представлена на рис. 4.
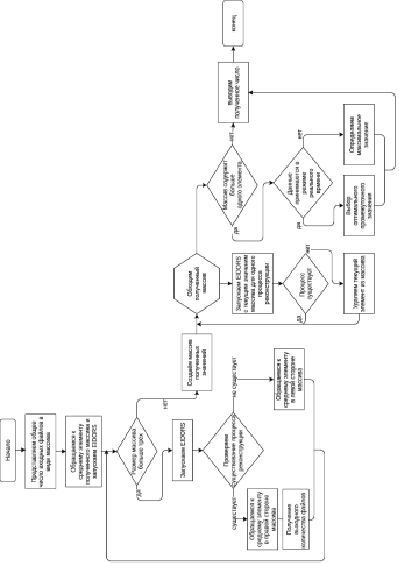
Рис. 4. Блок-схема работы алгоритма поиска n
Как видно из представленной на рис. 4 блок-схемы, разработанный алгоритм может быть применен при каждом запуске процесса реконструкции, позволяя значительно сокращать связанные с ней временные затраты без риска возникновения аварийных ситуаций, связанных с переполнением ОЗУ.
Результаты исследования и их обсуждение
Разработанный алгоритм позволяет определять максимальное n для достижения минимальной длительности процесса реконструкции и визуализации уже полученных входных файлов. При получении входных файлов в режиме реального времени (со скоростью 20–60 кадров в секунду [11]), производится выбор такого значения n, которое позволяет снизить время ожидания при получении входных файлов для процесса реконструкции и тем самым избежать увеличения времени задержки процесса выполнения реконструкции EIDORS и, соответственно, потери диагностической ценности реконструированных изображений.
Заключение
Таким образом, в рамках проведенного исследования разработан алгоритм поиска значения числа входных данных для одного томографического среза. Программное обеспечение, реализующее данный алгоритм, позволяет увеличить скорость обработки входных данных путём определения максимального количества входных файлов, прием которого программным компонентом АПК ЭИТ БО на имеющейся конфигурации ЭВМ возможен без риска превышения объема выделяемой ОЗУ и, как следствие, аварийного завершения работы процесса реконструкции.
При разработке данного алгоритма были проведены исследования на ЭВМ двух распространенных конфигураций по оценке средней нагрузки процесса реконструкции и числа файлов для процесса реконструкции, которое позволит значительно увеличить скорость визуализации реконструированных изображений при сохранении допустимого показателя временной задержки, связанной с выполнением процесса EIDORS как для двухмерной, так и трехмерной ЭИТ.
Проведенное исследование позволяет определить число входных данных для процесса реконструкции, как для уже полученных архивных данных, так и данных, получаемых в режиме реального времени в задачах МРЭИТ.
Направлением дальнейших исследований является оптимизация используемых алгоритмов реконструкции для задач МРЭИТ. Полученные результаты найдут применение в последующих исследованиях по разработке технических средств двухмерной и трехмерной ЭИТ.
Работы выполняются в рамках гранта Президента Российской Федерации для государственной поддержки молодых российских ученых МК-196.2017.8 «Разработка теоретических основ и алгоритмов многоракурсной электроимпедансной томографии для систем неинвазивной трехмерной медицинской визуализации».
Библиографическая ссылка
Алексанян Г.К., Щербаков И.Д., Сулыз А.В., Тетелев М.В. ПРОБЛЕМЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ РЕКОНСТРУКЦИИ МНОГОРАКУРСНОЙ ЭЛЕКТРОИМПЕДАНСНОЙ ТОМОГРАФИИ // Современные наукоемкие технологии. 2019. № 12-2. С. 243-248;URL: https://top-technologies.ru/ru/article/view?id=37866 (дата обращения: 09.03.2026).
DOI: https://doi.org/10.17513/snt.37866



