Динамично развивающееся общество нуждается в грамотных специалистах, которые обладают широким спектром профессиональных знаний и умений, готовы и способны качественно решать профессиональные задачи. Особо востребованы на рынке труда в настоящее время выпускники вузов, на базе которых ведется подготовка студентов естественно-технических профилей. Необходимым компонентом обучения студентов названных профилей является обучение математике. Основной целью этого обучения является формирование компетенций в области использования и разработки математических моделей, которые находят применение в определенной профессиональной сфере. Поэтому проблема поиска путей, методов, средств, разработка технологий качественной математической подготовки студентов названных профилей является актуальной.
В соответствии с федеральным государственным образовательным стандартом высшего образования реализация учебного процесса должна предусматривать проведение занятий в интерактивных и активных формах и методах обучения с целью формирования необходимых профессиональных компетенций [1–3].
Активные формы и методы обучения характеризуются равным участием студентов и преподавателя в проведении занятий. Их применение базируется на демократическом стиле педагогического общения. Интерактивные формы и методы во многом аналогичны активным и предполагают интенсивное взаимодействие всех студентов с преподавателем. Однако можно выделить несколько ключевых отличий. Во-первых, применение интерактивных форм и методов характеризуется тем, что именно обучаемым отводится ведущая роль, наставник только «направляет» их работу. Во-вторых, на занятии в основе организации лежат преимущественно активные методы, а взаимодействие студентов друг с другом проявляется не так явно, как в случае интерактивного взаимодействия.
Интерактивные формы и методы обучения являются основой интерактивных технологий [3–7]. Данные технологии предполагают поэтапное включение в учебный процесс специально разработанных кейсов - «комплектов учебно-методических материалов, разработанных на основе практических ситуаций, формирующих у обучающихся навыки самостоятельного конструирования способов решения задач» [8, с. 216]. Одной из особенностей таких комплектов является наличие подзадач, решение каждой из которых служит основой для решения последующей.
Цель исследования: выявить возможности применения интерактивных кейс-технологий в обучении математике студентов естественно-технических профилей.
Материалы и методы исследования
Исследование проводилось на основе применения теоретических (изучение и анализ психолого-педагогической, научно-методической и учебной литературы, в частности исследование образовательных программ бакалавриата естественно-технических профилей, в частности математических дисциплин) и эмпирических (наблюдение, беседа со студентами и преподавателями вузов) методов. Для изучения особенностей использования кейс-технологий в обучении студентов исследование проводилось на базе естественно-технологического факультета ФГБОУ ВО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», материально-техническое, аппаратно-программное и организационно-методическое обеспечение которых позволили определить потенциальные возможности и перспективы интерактивного обучения в вузе. Для описания содержания обучения с использованием кейсов и выявления оптимальных условий его реализации в контексте обучения в высшей школе использовался деятельностный подход [9].
Материалы статьи обладают практической значимостью для преподавателей математических дисциплин в контексте интерактивного обучения студентов вузов.
Результаты исследования и их обсуждение
Применение кейс-технологий связано с использованием в обучении конкретных ситуаций, описания которых заранее подготовлены преподавателем. Очень часто преподаватель заготавливает целую цепочку ситуаций, выстроенных так, что решение каждой последующей непосредственно связано с решением предыдущей. Предлагаемые к изучению ситуации можно разделить на четыре группы: ситуации-проблемы, ситуации-оценки, ситуации-иллюстрации, ситуации-опережения [10]. В первом случае ситуации связаны с конкретной практической проблемой, оценив которую студенты предлагают решения, если таковое вообще существует.
Ситуации-оценки – это описание проблемы с уже готовым вариантом ее решения. Студентам остается лишь оценить его. Ситуация-иллюстрация требует от учащихся подробного описания имеющегося положения дел, причин по которым она возникла. Также разрешение этой ситуации предполагает описание поиска ее решения и его алгоритма. Студенты должны всесторонне и с максимальной объективностью проанализировать ситуацию, сформулировать систему вопросов, позволяющих выбрать наиболее рациональное решение. Ситуации, решение которых основывается на применении уже приобретенных знаний и умений, называются ситуациями-опережениями.
В интерактивном обучении студентов важны все четыре вида описанных ситуаций, необходимо их поэтапное использование. Приведем примеры таких кейсов, в которых последовательно отражены ситуации-иллюстрации, ситуации-проблемы, ситуации-оценки и ситуации-опережения, разработанные в соответствии с рекомендациями, представленными в [11, 12].
Задание 1.
Заказчик обратился в инженерно-строительную компанию в связи с вопросом, возникшим у него при строительстве газопровода. В проектной документации, в соответствии с которой идет строительство газопровода, отсутствовал расчет величины прогиба трубы в пролете между опорами А и В, которые расположены, по сравнению с остальными опорами, на значительном расстоянии друг от друга. Кроме того, на этом участке труба будет подвергаться нагрузкам из-за близкого расположения к железной дороге. Заказчик обеспокоен потенциальной опасностью экологической катастрофы и собирается установить дополнительную опору между А и В, но где конкретно это необходимо сделать, не знает. Значение прогиба трубы в точке, расположенной правее опоры А на расстоянии х от нее, определяется по формуле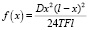 
, где значения T и F зависят от материала изготовления трубы и ее диаметра, l – длина части нефтепровода между А и В. Проведя новый расчет, инженер дал рекомендацию по установке дополнительной опоры на расстоянии 
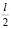правее А.
1. Проанализируйте описанную ситуацию. 2. На основании чего инженер предоставил рекомендацию? 3. В соответствии с представленными данными проведите исследование прогиба трубы и докажите или опровергните заключение сотрудника инженерно-строительной компании. 4. При каких вариантах установки дополнительной опоры риск экологической катастрофы не сводится к минимуму?
Приведем вариант решения данного кейса.
1. Фактически решение кейса сводится к исследованию экстремумов функции f(x) на отрезке [0; l].
2. Инженер мог предоставить рекомендацию, проанализировав функцию f(x) на экстремум и выявив точку максимального прогиба.
3. Проведем исследование функции f(x) на экстремум. Исходя из описанной ситуации, необходимо найти максимум названной функции на отрезке [0; l]. Вычисляем производную функции: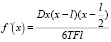 
. Отсюда получаем точки, подозрительные на экстремум: 
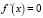при x1 = l, 
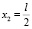, x1 = 0. Вычислим значения функции в точках 0, l и сравним их: f(1) = 0, f(0) = 0. При 
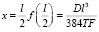. Таким образом, деформация газопровода будет наибольшей при 
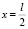. Заключение инженера истинно.
4. Риск экологической катастрофы не сводится к минимуму в том случае, если координата дополнительной опоры будет удовлетворять неравенствам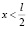 
или 
.
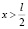Задание 2.
На одном из берегов реки располагается склад А, но подъезд к нему очень неудобный и опасный – на пути располагается множество мест, где могут произойти обвалы горной породы. В связи с этим было решено построить новый склад – В на другом берегу реки. После того, как новое место хранения было построено, владельцы задумались, как с наименьшими затратами перевезти материал из А в В. Организовать паромную переправу не представляется возможным, а переезжать реку через уже построенный мост за несколько километров затратно. Очевидна необходимость постройки временного моста.
1. Проанализируйте описанную ситуацию. 2. Сформулируйте условие, при котором затраты на перевозку будут минимальными (все автомобили одинаковы, заправляются одинаковым топливом и замене не подлежат). Поставьте вопрос, ответ на который необходимо дать для достижимости условия. 3. Найдите ответ на поставленный вопрос. 4. После того, как оптимальное решение будет найдено, ответьте на следующий вопрос. Предположим, возникла необходимость транспортировать кран-погрузчик со склада А на склад В. При движении кран может поворачивать только на угол 90 градусов. В соответствии с этим было решено организовать маршрут крана следующим образом: от пункта А до берега реки, далее к мосту, через мост на другой берег, от моста по берегу до точки, расстояние от которой до В будет минимальным, в пункт В. Каким соотношением в этом случае связаны расстояния, которые погрузчик пройдет по береговым линиям с расстояниями, которые он пройдет, двигаясь от склада А к берегу реки и от другого берега реки ко второму складу?
Далее представим один из возможных вариантов решения данного кейса.
1. Сделаем чертеж, который соответствует описанной ситуации (рисунок). Здесь А и В – склады, CD – мост через реку. Очевидно, что по условию значения a, b, c, h неизменны.
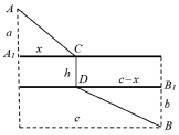
Схема расположения складов A, B и моста через реку CD
2. Затраты на перевозку при заданных условиях будут минимальны в том случае, если маршрут автомобилей, перевозящих материалы из А в В, будет минимальным по расстоянию. Таким образом, необходимо найти такое место для постройки моста, чтобы выполнялось указанное выше условие.
3. Если все объекты на местности расположены так же, как и на чертеже, то весь путь от А к В равен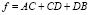 
. Обозначив за x длину отрезка A1C, получим: 
, 
, 
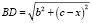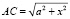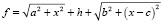, причем 
.
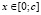Найдем минимум функции f(x) на указанном отрезке.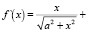 
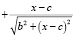. Решая уравнение 
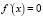, получаем точки, подозрительные на экстремум: 
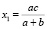и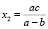 
. Вторая точка расположена вне рассматриваемого отрезка, первая – на отрезке (поскольку x1 > 0, 
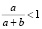, следовательно, x1 < c). Применяя достаточные признаки возрастания и убывания функции, убеждаемся, что x1 - точка минимума.
Таким образом, чтобы длина маршрута была минимальной, необходимо построить мост там, где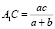 
.
4. В соответствии с чертежом необходимо указать соотношение, которым связаны значения x, c – x, a, и b в том случае, когда мост построен в соответствии с найденным решением. Нетрудно проверить, что в этом случае a(c – x) = bx.
Задание 3.
Фабрика, выпускающая сотовые телефоны, не работала длительное время, в связи с чем при ее запуске было разработано новое планирование хозяйственной деятельности. В соответствии с ним в первый год фабрика должна будет выпустить 31000 телефонов. Каждый год количество товара будет увеличиваться на 500 единиц. Владелец решил зарезервировать часть средств в сумме 100 000 руб. для реализации последующих амортизационных отчислений в течение 10 лет.
1. Проанализируйте описанную ситуацию. 2. Будет ли достаточно зарезервированной владельцем суммы для покрытия амортизации за 10 лет, если норма отчислений за каждый год составляет 1 % от стоимости товара при стоимости телефона 50 рублей? 3. Какое количество амортизационных сумм за 10 лет будет достаточным для покупки телефонов, выпущенных за аналогичный период? Эффективна ли норма амортизации, предложенная в предыдущем пункте в случае, если количество непроданных телефонов составляет не более 20 % от выпущенных?
Использование представленных кейсов позволит преподавателю выстроить структуру занятия, позволяющую в наиболее полной степени реализовать принцип индивидуального подхода, при этом поддерживая высокую связь обучения с практикой [13].
Ситуации, подобные описанным выше, имеют прикладное содержание. При обсуждении решения кейсов обучающиеся могут свободно привлекать собственный жизненный опыт и кругозор. Так, на заключительном этапе работы с предложенной ситуацией необходимо соотнести построенную математическую модель с элементами реального образа, сформированного в воображении и основывающегося на реальном опыте.
Работа над представленными заданиями может быть организована с привлечением метода мозгового штурма. Это способствует развитию гибкости мышления студентов, позволяет находить решения в различных ситуациях, обеспечивает возможность широкого взаимодействия обучающихся между собой.
Заключение
Применение кейс-технологий в обучении математике студентов естественно-технических профилей, прежде всего, основано на включении в учебный процесс кейсов – конкретных ситуаций четырех видов, описанных выше. Методика работы с этими комплектами заданий предполагает интерактивное взаимодействие студентов между собой и преподавателем. Выполнение предлагаемых кейсов благотворно развивает у обучающихся умения анализировать ситуации, дает им возможность оценивать альтернативные решения, выбирать из них наиболее оптимальное и осуществлять его.
Таким образом, у студентов формируются умения работать в команде, развиваются способности обосновать и представлять результаты своей деятельности. Предлагаемые нами интерактивные технологии позволят им в будущем успешно моделировать свое профессиональное поведение, обусловят их востребованность и успешное трудоустройство.
Статья выполнена в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов-партнеров по сетевому взаимодействию (Пермский государственный гуманитарно-педагогический университет и Мордовский государственный педагогический институт им. М.Е. Евсевьева) по теме «Технология математической подготовки студентов естественно-технических профилей в условиях бакалавриата».
Библиографическая ссылка
Сарванова Ж.А., Кочетова И.В., Дорофеев С.Н., Порваткин А.В. КЕЙС-ТЕХНОЛОГИИ В ИНТЕРАКТИВНОМ ОБУЧЕНИИ МАТЕМАТИЧЕСКИМ ДИСЦИПЛИНАМ СТУДЕНТОВ ЕСТЕСТВЕННО-ТЕХНИЧЕСКИХ ПРОФИЛЕЙ // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 195-199;URL: https://top-technologies.ru/ru/article/view?id=37858 (дата обращения: 21.11.2024).