Уникальными прочностными и эксплуатационными свойствами конструкционных углеродистых сталей, как правило, пренебрегают при получении сварных конструкций. Причинами отказа от использования этих сталей в сварке являются повышенная трудоемкость процесса, вследствие высокого углеродного эквивалента, который определяет склонность неразъемного соединения к образованию пор и трещин, являющихся следствием внутренних напряжений. Так как использование трудносвариваемых сталей с высоким углеродным эквивалентом ограничено при получении сварных конструкций недостаточно изученным представляется влияние локального нагрева на структуру и физико-механические свойства пластины. Актуальность исследований, связанных с изучением вопросов формирования и прогнозирования свойств материала, наплавляемого на поверхность углеродистой стали, определяется необходимостью получения неразъемного соединения с высокими прочностными и эксплуатационными характеристиками.
Сборка металлоконструкций из неразъемных соединений, полученных сваркой, в ряде случаев затрудняется по причине нарушения геометрической точности, являющейся следствием температурного градиента, приводящего к появлению закалочных структур. Изменения структуры в области активного теплового воздействия свидетельствуют о протекании в металле пластического течения. Температурные напряжения, как правило, концентрируются в окрестности области теплового воздействия, приводя к появлению дефектов. Металл в области пластического течения обладает иными механическими характеристиками в отличие от основного металла. Предварительными исследованиями установлено, что предел текучести в этой области увеличивается, что свидетельствует об упрочнении материала. Также возможно появление области разупрочнение металла [1, 2]. Упругие модули понижаются в области высокой температуры и восстановить прежние значения при остывании не могут, что объясняется фазовыми изменениями [3].
Таким образом, проблемой при проектировании сварных конструкций из указанных видов сталей является определение величины остаточных напряжений и деформаций в зоне интенсивного температурного влияния с целью их регулирования. Этой проблеме посвящено значительное число работ [4–6], в том числе и авторами настоящего исследования [7, 8]. В работе [9] представлены результаты математического моделирования процесса точечного нагрева диска с образованием наплава. Однако такое решение не совпадает со значениями остаточных напряжений, зарегистрированными на поверхности пластины, поэтому было принято решение усложнить математическую модель введением вязкости и упрочнения в пластическое течение и сравнить результаты расчетов с экспериментальными данными.
Недостаточный объем информации об экономической эффективности применения трудносвариваемых углеродистых сталей определяет целый ряд проблем, связанных с оптимизацией таких технологических параметров производства, как расход электродного материала; трудоемкость сварочных и слесарных работ (связанных с разделкой кромок, устранением окалины и т.д.). Недостаток практической составляющей в экономических расчетах такого плана и, как следствие, возможности прогноза расхода материалов, трудовых и временных затрат, определяют актуальность исследований, представленных в настоящей работе.
Цель исследования: разработка и экспериментальное подтверждение адекватной математической модели расчета остаточных напряжений в материале пластины из углеродистой стали со сварным наплавом на основе условия максимальных приведенных напряжений (Ишлинского – Ивлева) с введением слагаемых, отвечающих за упрочнение материала и вязкости при пластическом течении.
Материалы и методы исследования
В расчетах за основу математической модели принята модель Прандтля – Рейса, в которой деформации малы и складываются из обратимых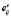 
и необратимых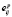 
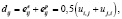(1)
где ui,j – компоненты вектора перемещений, dij – компоненты тензора полной деформации.
Обратимые деформации связаны с напряжениями σij и температурой T законом Дюамеля – Неймана [10]
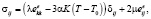(2)
σij – компоненты тензора напряжений, T, T0 – текущая и начальная температура, λ, μ, K – упругие модули, μ – модуль сдвига G,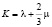 
– модуль всестороннего сжатия.
Необратимые деформации развиваются, если напряженное состояние достигнет поверхности нагружения согласно ассоциированному закону пластического течения [11]
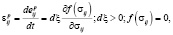(3)
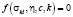– уравнения поверхности нагружения в пространстве напряжений, k – предел текучести материала, c, η – коэффициенты упрочнения и вязкости.
В качестве наступления пластического течения использовано условие максимальных приведенных напряжений Ишлинского – Ивлева) [12, c. 120]
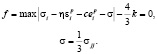(4)
Распределение температуры задается законом температуропроводности [13]
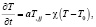(5)
где a – коэффициент температуропроводности, χ – коэффициент теплоодачи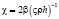 
β – коэффициент теплоотдачи от деформируемого и проводящего тепло тела в окружающую среду, ς – удельная теплоемкость на единицу массы, ρ – плотность материала пластины, h – толщина пластины.
Принимая во внимание высокую температуру нагрева материала, в отличие от классического случая теории температурных напряжений, задаваемой зависимостями (1)–(3), когда в них λ, μ, η, k постоянные величины, связали их зависимости от температуры
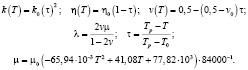(6)
В (6) k0, η0, v0, μ0 – предел текучести, коэффициенты вязкости, коэффициенты Пуассона, модуль сдвига при комнатной температуре, Tp – температура плавления металла.
Завершает систему уравнений (1–6) уравнение равновесия
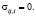(7)
Для проведения натурного эксперимента использовали пластины шириной 100 мм, длиной 200 мм, толщиной 12 мм, выполненные из конструкционной углеродистой стали 45 (ГОСТ 1050-2013). Остаточные напряжения определяли на рентгенодифрактометрическом анализаторе RIGAKU MSF-3M до начала теплового воздействия (с целью подтверждения малых значений напряжений) и после остывания. В центре пластины (рис. 1), помещали источник тепла (электрическая дуга) и производили нагрев до температуры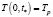 
с образованием сварного наплава, вследствие переноса присадочного материала в зону нагрева.
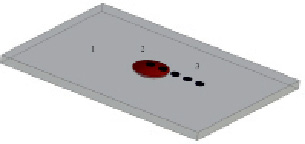
Рис. 1. Схема определения остаточных напряжений: 1 – стальная пластина; 2 – место наплавки; 3 – точки снятия данных
Для проверки теоретических расчетов математической модели и определения влияния теплового воздействия электрической дуги опытные испытания проводили на универсальной машине AG-X plus SHIMADZU при постоянной скорости перемещения захватов 0,05 мм/c.
Результаты исследования и их обсуждение
При постановке задачи с упругим деформированием в цилиндрической системе координат (r, φ, z) располагаем пластину, которая нагревается от источника тепла, находящегося в центре r = 0
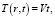
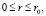(8)
где V – скорость нагрева, r0 – радиус пятна нагрева. Когда температура в центре пластины станет равной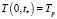 
– источник тепла отводится и материал пластины остывает.
Теплоотводом от боковых поверхностей пластины пренебрегаем из-за малой толщины. Распределение температуры в материале пластины во время исследования определяется из закона теплопроводности (5) в цилиндрической системе координат
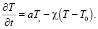(9)
Поскольку решения температурной задачи (8)–(10) получают с помощью численных методов [13, с. 6] или аналитически [14, с. 53], то переходим к механической задаче.
В условиях плоского напряженного состояния (σz = 0) из зависимостей закона Дюамеля – Неймана имеем
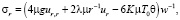
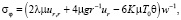
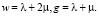(10)
Подстановка (10) в уравнение равновесия
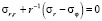(11)
приводит к уравнению для вычисления перемещения ur
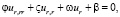(12)
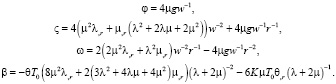
В качестве граничных условий выбираем условия
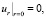
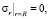(13)
где R – расстояние до края пластины.
В случае зависимости упругих модулей от температуры решить дифференциальное уравнение (12) совместно с граничными условиями (13) возможно только численно. Аналитическое решение при постоянных упругих модулях приведено в [9].
С некоторого момента в центре нагрева выполнится условие пластического течения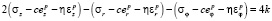 
. Образуется упругопластическая граница r = n1(t). В области 
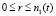материал пластически течет, образуются и развиваются необратимые деформации. Закон Дюамеля – Неймана запишется в виде
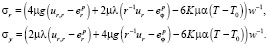(14)
Из ассоциированного закона пластического течения (3) находим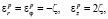 
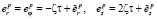. Слагаемые ζτ являются приращением необратимой деформации 
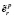, существовавшей или зародившейся на предыдущем временном шаге, τ = ?t – шаг по времени. Выражаем ζ:
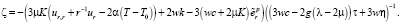(15)
Решая численно уравнение равновесия (11) в области пластического течения с учетом (14) и (15) на каждом временном шаге находятся перемещения.
После отвода тепла в центре r = 0 необратимые деформации замедляют свой рост, образуется разгружающая упругопластическая граница r = m1(t). Здесь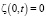 
. Эта граница продвигается за границей r = n1(t), и через некоторый промежуток времени границы соединяются. В области разгрузки 
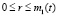границы определяются из соотношений (14). Упругие модули (6) сохраняют значения при остывании, что моделирует фазовые переходы.
С распределением температуры пластины в области нагрева r = 0 выполнится условие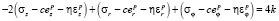 
; здесь зарождается повторное пластическое течение с границей r = n2(t), которое продвигается по материалу пластины до момента остывания. Остывание пластины приводит к затуханию пластического течения. Разгружающая упругопластическая граница r = m2(t) образуется в центре 
(
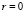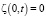). При полном остывании границы m2(t) и n2(t) соединятся. Распределения перемещения в материале пластины находятся численно из решения дифференциального уравнения равновесия (11). На рис. 2 показаны распределения напряжений для пластин. Экспериментальные значения остаточных напряжений изображены на графиках точками и лежат в области полученных теоретических кривых, что подтверждает работоспособность математической модели.
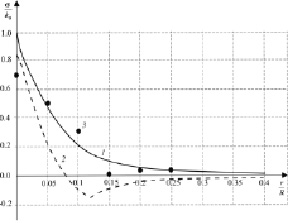
Рис. 2. Распределение остаточных напряжений в материале пластины из стали 45: 1 – σrr , 2 – σφφ , 3 – σrr (полученное в ходе натурного эксперимента)
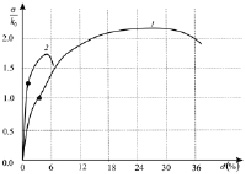
Рис. 3. Диаграмма деформирования: 1 – до нагрева, 2 – после нагрева
Локальный нагрев оказывает влияние на структуру и физико-механические свойства материала пластины из углеродистой стали. Тепловое воздействие электрической дуги нагревает металл до температуры плавления в зоне контакта. При остывании в точке наплавления металла появляются высокие растягивающие напряжения.
Данные изменения происходят из-за перегрева металла и впоследствии его быстрого охлаждения, что приводит к росту остаточных напряжений в металле. Это оказывает влияние на физико-механические свойства материала пластины и приводит к его упрочнению в зоне теплового воздействия. Образцы до и после теплового воздействия подвергались испытанию на растяжение (рис. 3). Из рис. 3 видно, что после воздействия электрической дуги на пластину предел текучести растет со снижением предела прочности.
При расчете экономической эффективности использования результатов, представленных в настоящей работе исследований, следует учитывать снижение трудозатрат при проектировании конструкций, узлы которых получены из сталей с высоким углеродным эквивалентом. Использование результатов исследований не предполагает замену или модернизацию оборудования, и направлено на получение эффекта в виде снижения затрат на эксперименты при технологической проработке партии изделий из конкретной марки трудносвариваемой стали.
В конечном счете экономическая целесообразность результатов определяется сокращением расхода электрической энергии на получение бездефектного сварного соединения с глубоким проваром и меньшим короблением.
Выводы
С использованием условия максимальных приведенных напряжений (Ишлинского – Ивлева) с введением слагаемого, отвечающего за упрочнение материала и вязкости при пластическом течении, возможен расчет остаточных напряжений в материале пластины из углеродистой стали со сварным наплавом, что подтверждается натурным экспериментом. После проведения наплава в материале пластин повышается предел текучести, но при этом в несколько раз сокращается площадка текучести, что доказывает упрочнение материала пластины в результате проведения наплава.
Работа выполнена в рамках государственного задания № 075-00414-19-00.
Библиографическая ссылка
Ткачева А.В., Абашкин Е.Е., Жилин С.Г., Комаров О.Н. ФОРМИРОВАНИЕ ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ В ПЛАСТИНЕ ИЗ УГЛЕРОДИСТОЙ СТАЛИ СО СВАРНЫМ НАПЛАВОМ // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 99-104;URL: https://top-technologies.ru/ru/article/view?id=37841 (дата обращения: 19.04.2024).