В условиях интенсивного развития технологического базиса и информационной инфраструктуры постиндустриального общества на основе комплексного освоения нано-, био-, когнитивных и информационных технологий существенно обострилась проблема информационной безопасности. Закономерным результатом эволюции корпоративных средств защиты информации в информационно-вычислительных сетях (ИВС) стало создание систем комплексной защиты сетевых ресурсов [1], построенных на основе ведущих принципов системного подхода, кибернетики и искусственного интеллекта.
Один из перспективных подходов к задачам информационной безопасности ИВС заключается в осуществлении концепции ситуационного управления информационными рисками [2]. На эффективность реализации технологии управления информационными рисками существенное влияние оказывает используемый способ динамического распределения сетевых ресурсов. В авторской работе [3] c позиций ситуационного управления рисками информационной безопасности выделена частная задача синтеза механизма динамического управления сетевыми ресурсами и показана возможность её решения на основе применения моделей и методов математического программирования. Создание и реализация в ИВС специальных механизмов целенаправленного перераспределения информационных и программных ресурсов способствуют повышению гибкости и устойчивости информационной инфраструктуры предприятий к воздействию деструктивных факторов различной физической природы.
Цель статьи: обоснование алгоритмического подхода к формализации задачи оптимального распределения компонентов специального программного обеспечения в узлах корпоративной ИВС на основе методов дискретного программирования.
Концепция динамического распределения программных ресурсов
В качестве объекта исследования в настоящей работе рассматривается динамично расширяющийся сегмент корпоративной ИВС. В составе его аппаратной платформы выделим центры обработки данных, телекоммуникационную сеть, включающую каналы связи, узлы связи и комплект дополнительного оборудования, а также узлы подключения коллективных пользователей. Представим с общих позиций постановку задачи распределения программных ресурсов в узлах сегмента корпоративной ИВС.
Пусть на конкретном этапе развития (или модернизации) корпоративной ИВС необходимо решить задачу выбора оптимального плана размещения комплексов специализированных программных средств (КПС) на конечном множестве узлов.
Примем следующие обозначения:
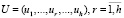– множество узлов сегмента ИВС;
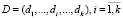– множество информационных услуг (сервисов), предоставляемых конечным пользователям комплексом программных средств, реализованном на аппаратной платформе (в узле) сегмента ИВС;
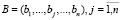– множество комплексов программных средств, предлагаемых для установки в узлах ur;
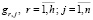– материальные затраты на установку КПС bj в узле ur;
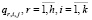– материальные затраты на предоставление установленным программным средством bj, размещённым на узле ur, информационной услуги di для реализации соответствующего сервиса.
Дополнительно введём следующие переменные:
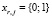– булева переменная, указывающая, входит (1) или нет (0) КПС bj в состав программного обеспечения узла ur;
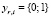– булева переменная, указывающая на возможность использования оборудования узла ur для предоставления услуги di.
С учётом принятых обозначений для конкретного узла ur сети определим суммарные затраты на установку, обслуживание и использование программного обеспечения:
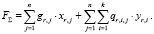(1)
Здесь
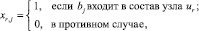
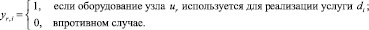
Функциональность и производительность конкретного КПС рассчитана на оказание определённого набора информационных услуг пользователям, поэтому следует предусмотреть минимальное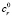 
и максимальное 
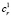количество услуг, предоставляемых оборудованием узла ur конечному пользователю. Для этого введём областное ограничение в виде неравенства
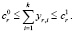(2)
Далее введём дисциплинирующее условие
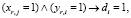(3)
которое означает, что услуга di может быть предоставлена программным средством bj, если это средство введено в состав программного обеспечения узла ur.
Учитывая конечное значение вычислительной мощности каждого узла ur, предусмотрим ограничение на размещение программных средств:
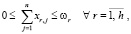(4)
где ωr – допустимое количество единиц комплексов программных средств, которые могут быть установлены в узле ur.
Формальная модель задачи выбора плана x* размещения программных средств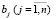 
в узлах сети 
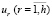может быть представлена в двух вариантах.
В первом случае рассматривается задача поиска оптимального плана x* размещения программных средств, при котором обеспечивается минимальная величина риска R(x*) невыполнения запросов пользователей сети, а совокупные затраты F(x, y) на установку и сервисное обслуживание программного обеспечения не превышают допустимого уровня CД:
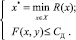
Во втором случае задача выбора оптимального плана заключается в определении такого плана размещения программных средств x*, при котором совокупные затраты на установку и использование ресурсов минимальны, а величина риска R(x*) невыполнения запросов пользователей находится в допустимых пределах
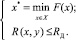
Здесь CД и RД – соответственно допустимое значение затрат и верхний пороговый уровень риска, задаваемые с учётом специфики сети и системных требований к функциональности оборудования и программного обеспечения.
Функцию риска R(x, y) в силу необходимости учёта большого числа факторов и нечёткости задания исходных данных следует отнести к классу невыпуклых функций, которую достаточно сложно представить в явном виде. Поэтому с прагматической точки зрения более предпочтительным является второй вариант постановки задачи. При этом функционал совокупных затрат F(x, y) рассматривается как целевая функция экстремальной задачи, а функция риска R(x, y) может быть интерпретирована либо как количество нереализованных услуг, либо как величина ущерба, обусловленного невыполнением заказа на обслуживание. Иными словами, ограничение на величину риска можно представить как дополнительное функциональное ограничение.
С учётом введённых выше обозначений совокупные затраты на размещение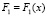 
и поддержку 
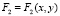программных ресурсов в узлах сети зададим с помощью обобщённого показателя
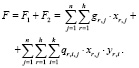(5)
В соответствии с изложенными выше положениями предпочтительным будет такой план размещения программных ресурсов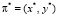 
в узлах сети, для которого значение обобщённого показателя совокупных затрат (5) является наименьшим при условии выполнения всех ограничений. В нашем случае для определения плана 
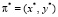размещения КПС в узлах ИВС требуется найти численное решение задачи дискретного программирования (в булевых переменных). Оптимальным считается такой план размещения заданного набора КПС в узлах выделенного сегмента сети, при котором удовлетворяются все дисциплинирующие условия, а совокупные затраты, определяемые показателем (5), минимальны.
Модель прикладной задачи распределения ресурсов
В соответствии с принятой в теории математического программирования терминологией сформулированная выше задача может быть отнесена к комбинаторным задачам о назначениях [4; 5].
Специфику формальной модели рассматриваемой прикладной задачи определяют следующие особенности:
1) бинарное представление векторов управляемых {xr,j} и вспомогательных {yr,i}переменных;
2) несоответствие числа КПС и количества узлов ИВС (т.е. n ≠ h), выделяемых для их размещения; формально это положение отразим в виде областных ограни-чений, накладываемых на вектор управляемых параметров:
;
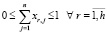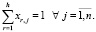(6)
2) наличие логических дисциплинирующих условий, определяющих допустимые правила распределения ресурсов;
3) введение дополнительных нелинейных функциональных ограничений, регламентирующих затраты на обслуживание размещенных в узлах программных средств и на величину допустимого ущерба от нереализованных информационных услуг.
Указанные выше признаки дают основание классифицировать рассмотренную задачу о размещении КПС в узлах сегмента ИВС как специальный вид канонической задачи о назначениях. В настоящее время в литературе нашли отражение различные модификации канонической задачи о назначениях [5; 6].
Для экспериментальной проверки и конкретизации предложенного автором методического подхода выполнена параметризация изложенной модели задачи. Сформулируем прикладную задачу выбора оптимального плана размещения КПС на конечном множестве узлов сегмента ИВС.
Пусть выделен сегмент корпоративной ИВС и задана его конфигурация в виде n = 8 узлов и связей между ними. На существующей аппаратной платформе следует разместить h = 6 комплексов программных средств, которые могут дополнительно предоставить пользователям k = 10 информационных услуг.
Требуется определить такой план размещения КПС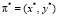 
, для которого показатель затрат принимает минимальное значение 
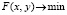, а величина совокупного риска (ущерба) невыполнения запроса на обслуживание не превышает допустимого уровня 
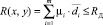. Здесь 
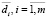– нереализованные информационные услуги, μi – весовой коэффициент нереализованной услуги di.
Процесс определения плана размещения программных средств в комбинаторной задаче существенно зависит от размерности переменных x и y, которые в нашем случае представляют собой прямоугольные матрицы размером (8×6) и (8×10) соответственно. Для указанных условий задачи размерность вектора изменяемых параметров составит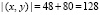 
единиц. В интересах обеспечения вычислительной устойчивости процесса поиска численного решения уменьшим размерность вектора переменных параметров путём изменения структуры критерия оптимальности (5), исключив из него составляющую 
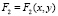, содержащую компоненту 
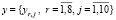. При этом показатель затрат на оказание услуг перемещёнными средствами переведём в разряд функциональных ограничений
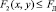. (7)
Тогда задача дискретной оптимизации будет заключаться в минимизации функционала:
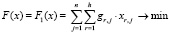(8)
с учётом областных ограничений (2), (3), (6) и дополнительного функционального ограничения (7).
Примем также условие, что затраты на реализацию информационной услуги зависят от конкретного узла, в котором размещено программное средство. Дополнительно будем считать, бинарная матрица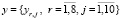 
априорно задана. Указанные допущения позволяют заменить трёхмерную матрицу затрат Q = {qr,i,j} в выражении (7) на прямоугольную матрицу затрат Q = {qr,i}.
Результаты численного решения прикладной задачи
Исходные данные для решения сформулированной прикладной задачи представлены в табл. 1–4.
Таблица 1
Матрица затрат на установку оборудования G = {gr,j}T
|
r \ j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
41 |
38 |
58 |
34 |
25 |
30 |
40 |
56 |
|
2 |
45 |
42 |
52 |
41 |
24 |
24 |
34 |
28 |
|
3 |
57 |
20 |
45 |
68 |
35 |
25 |
21 |
45 |
|
4 |
34 |
24 |
72 |
30 |
18 |
50 |
25 |
37 |
|
5 |
39 |
21 |
38 |
50 |
40 |
38 |
53 |
32 |
|
6 |
24 |
40 |
15 |
26 |
30 |
12 |
35 |
18 |
Таблица 2
Матрица затрат на предоставление услуг Q = {qr,i}
|
r \ i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
3 |
10 |
12 |
1 |
14 |
21 |
4 |
6 |
2 |
9 |
|
2 |
5 |
6 |
10 |
1 |
12 |
12 |
6 |
6 |
8 |
7 |
|
3 |
6 |
10 |
9 |
2 |
11 |
10 |
5 |
7 |
7 |
6 |
|
4 |
11 |
12 |
10 |
1 |
15 |
8 |
7 |
5 |
5 |
8 |
|
5 |
8 |
10 |
12 |
4 |
13 |
10 |
2 |
8 |
1 |
3 |
|
6 |
4 |
7 |
10 |
5 |
15 |
4 |
8 |
4 |
4 |
5 |
|
7 |
7 |
6 |
11 |
2 |
14 |
11 |
6 |
1 |
2 |
6 |
|
8 |
6 |
15 |
10 |
3 |
12 |
8 |
9 |
9 |
3 |
8 |
Таблица 3
Опорный план предоставления услуг узлами y* = {yr,i}
|
r \ i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
2 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
4 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
5 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
6 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
7 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
8 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Таблица 4
Опорный план закрепления оборудования x0 = {xr,j}T
|
j \ r |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
Элемент G = {gi,j} матрицы затрат (табл. 1) на установку показывает в абсолютных единицах стоимости величину затрат на установку i-го КПС в j-м узле сегмента ИВС.
Опорному плану закрепления программных средств (табл. 4) соответствует значение показателя совокупных затрат F(x) = F1(x) = 209 у.е., вычисленного по формуле (8). Совокупные затраты на реализацию сервисных услуг составили F2(x) = 179 у.е.
Для численного решения прикладной задачи определения плана распределения КПС применён метод дискретного случайного поиска, разработанный И.В. Сергиенко [7], многократно показавший на практике высокую эффективность при решении комбинаторных задач целочисленной оптимизации. В ходе вычислительного эксперимента получен план, представленный в виде матрицы x* закрепления КПС за узлами сегмента сети (табл. 5). Указанному оптимальному решению прикладной задачи соответствует значение критерия затрат F(x) = F1(x) = 144 у.е.
Таблица 5
Оптимальный план x* размещения КПС в узлах сети
|
j \ r |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
Совокупные затраты на реализацию сервисных услуг по запросам пользователей, как показали расчеты, при реализации оптимального плана распределения не превышают F2(x, y) = 171 у.е.
Таким образом, в результате численного решения специальной задачи о назначениях в булевых переменных был получен оптимальный план размещения КПС в узлах ИВС (табл. 5). Согласно найденному решению предлагается разместить КПС в узлах: 2, 3, 4, 5, 6, и 7. Осуществление полученного плана позволит реализовать заданный комплекс информационных услуг при минимальных затратах на установку КПС (табл. 4) и допустимых ограничениях на стоимость обслуживания программных средств. В случае использования плана x* размещения КПС уровень затрат на установку КПС снизится (по отношению к исходному опорному плану (табл. 4)) на 31,1 %.
Заключение
В основе предложенного алгоритмического подхода лежит процедура преобразования формальной модели задачи распределения программных средств к задаче о назначениях специального типа. В рассмотренной прикладной задаче минимизируются затраты на установку программных средств с учетом ограничений, которые накладываются на стоимость обслуживания программных средств и величину ущерба, обусловленного сокращением номенклатуры информационных услуг, предоставляемых конечным пользователям. Для получения более корректных результатов и формирования на их основе практических рекомендаций по динамическому распределению компонентов специального программного обеспечения на сегменте ИВС необходимо конкретизировать исходные данные (табл. 1–3), а методику расчета показателей затрат дополнить детализированной топологической моделью сегмента ИВС. В качестве направления дальнейших исследований можно указать обоснование рационального способа дифференцированного учета функциональности отдельных КПС.
Библиографическая ссылка
Надеждин Е.Н. ЗАДАЧА РАСПРЕДЕЛЕНИЯ ПРОГРАММНЫХ РЕСУРСОВ ИНФОРМАЦИОННО-ВЫЧИСЛИТЕЛЬНОЙ СЕТИ // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 89-94;URL: https://top-technologies.ru/ru/article/view?id=37839 (дата обращения: 19.04.2024).