Повышение глубины переработки нефти – задача государственного значения, которая в настоящее время решается путем широкомасштабной модернизации нефтеперерабатывающих производств [1, 2]. На современном этапе развития нефтеперерабатывающей промышленности повышение глубины переработки нефти достигается за счет введения в эксплуатацию гидрогенизационных процессов, включая процесс гидрокрекинга, позволяющего перерабатывать тяжелые вакуумные дистилляты и получать высокий выход качественных моторных топлив [3–5].
Актуальность моделирования процессов глубокой переработки нефти, в частности гидрокрекинга, подтверждается необходимостью проведения данного процесса в наиболее оптимальных условиях с целью повышения эффективности деятельности предприятий нефтепереработки. В общем балансе предприятий нефтепереработки установка гидрокрекинга приносит до 40 % прибыли предприятия.
Гидрокрекинг – один из методов получения средних дистилляторов из тяжелой нефти и остатков [6].
Определение параметров кинетической модели на основе экспериментальных данных является достаточно трудоемкой работой.
Задачи оптимизации таких сложных процессов эффективно решаются на основе применения современных методов математического моделирования с использованием различных упрощений, например группировке индивидуальных реагентов в групповые псевдореагенты и группировке индивидуальных реакций в групповые реакции.
Математическое и компьютерное моделирование процесса гидрокрекинга заключается в систематическом подходе к кинетической и термодинамической подсистемам процесса переработки парафинов. Одна из проблем моделирования – широкий спектр компонентов в сырьевом и в продуктовом потоках.
В связи с этим моделирование сводится к созданию более ёмких псевдокомпонентов. Псевдокомпоненты позволяют осуществить нивелирование по некритичным составляющим, в свою очередь вывести закономерности по кинетике реакций крекинга [7].
Качество продукта переработки смеси углеводородов, предназначенного для использования в качестве бензинового топлива, оценивают с помощью октанового числа.
Октановое число – показатель, который характеризует детонационную стойкость топлива (бензина), применяемого в двигателях внутреннего сгорания с внешним смесеобразованием, то есть его устойчивость к воспламенению под высоким давлением.
Чем больше октановое число, тем выше детонационная стойкость, тем больше давления на него можно оказать, не вызывая детонации, то есть резкого возгорания. В современных автомобилях, где установлены двигатели внутреннего сгорания, октановое число является очень важным параметром, поскольку бензин с более низким ОЧ может серьёзно повредить поршни двигателя.
Октановое число равно содержанию (в % по объему) изооктана (i-C8H18) в его смеси с н-гептаном (у которого октановое число равно 0) при стандартных условиях испытания [8].
Цель исследования: разработка математической модели кинетики химических реакций гидрокрекинга индивидуальных углеводородов при условии протекания процесса в представлении состава смеси непрерывным
Материалы и методы исследования
Разработка непрерывных по составу моделей предполагает использование функций плотности распределения активации по некоторой выбранной переменной [6].
Выберем такой переменной температуру кипения молекулы.
Стехиометрическая модель реакций смеси н-парафинов при гидрокрекинге в терминах непрерывного состава соответствует схеме:
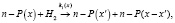 (1)
(1)
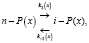 (2)
(2)
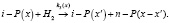 (3)
(3)
Кинетическая модель состоит из трех интегро-дифференциальных уравнений, первое из которых описывает крекинг и образование парафинов нормального строения, второе – изопарафинов и третье описывает расход водорода в системе:
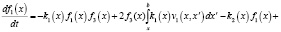
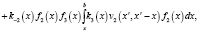 (4)
(4)
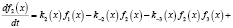
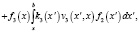 (5)
(5)
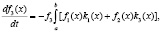 (6)
(6)
где x – переменная интервала a, b;
f1(x), f2(x), f3(x) – функции распределения состава нормальных парафинов, изопарфинов и количество водорода, соответственно;
vi(x) – матрица влияния, имеющая смысл вероятности разрыва связей C – C в молекуле с длиной цепи x' с образованием компонента с длиной цепи x;
ki(x) – константы скорости в зависимости от числа атомов углерода в реагирующей молекуле [6].
Начальные условия модели: t = 0, 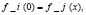
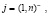
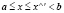 .
.
Для решения системы уравнений (4–6) использовался сравнительный анализ аналитического решения «Bench-mark experiment». Смысл этого метода заключается в фиксировании ядра компонентов, состоящего из вектора констант скорости математической модели (4)–(6). Фиксация ядра приводит к упрощению систем уравнений, превращая интегро-дифференциальные в обычные дифференциальные уравнения. В нашем случае фиксация происходит в точках k1(x), k2(x), k3(x), k-2(x), k-3(x).
Система уравнений (4)–(6) преобразуется в следующую систему:
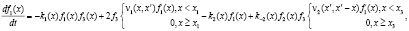 (7)
(7)
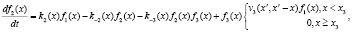 (8)
(8)
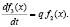 (9)
(9)
Рассмотрим случай, когда 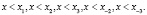
Предположим, что 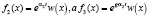 и подставив f2 и f3 в уравнение (8), получим
и подставив f2 и f3 в уравнение (8), получим
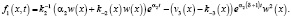
Приравняем уравнения (7) и (8) и подставим найденные ранее f1(x), f2(x) и f3(x). Получим
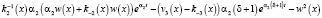 =
=
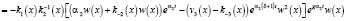
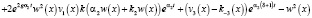 +
+
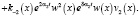
Объединив подобные элементы, уравнение преобразуется к виду
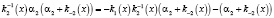
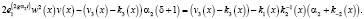 (10)
(10)
Таким образом, из уравнения (10) вытекают следующие равнозначные решения:
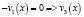 и
и 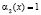 (11)
(11)
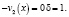 (12)
(12)
Взяв в качестве примера (12), получим аналитическое решение:
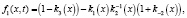 (13)
(13)
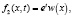 (14)
(14)
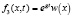 . (15)
. (15)
Результаты исследования и их обсуждение
В таблице представлены результаты расчета гидрокрекинга парафиновой фракции по модели (4)–(6). Расчет проводились для температуры T = 389,5 °C и давлении P = 40 атм. В первом и втором столбцах таблицы представлены названия и состав исходного сырья многокомпонентной смеси. В столбце 3 – состав продуктов, полученных в результате эксперимента нефтепереработки. В 4 – состав сырья, полученного в результате расчетов по математической модели.
Углеводородный состав сырья и продуктов гидрокрекинга смесей н-парафинов (T = 389,85 °C, P = 40 атм)
|
Углеводороды |
Сырье, % вес |
Продукты, % вес |
|
|
Эксперимент |
расчетные |
||
|
водород |
100 |
50 |
58,356 |
|
метан |
0 |
0,55 |
0 |
|
этан |
0 |
2,7 |
0 |
|
пропан |
0 |
15,25 |
0 |
|
изобутан |
0 |
10,87 |
8,4 |
|
бутан |
10 |
14,42 |
12,4 |
|
изопентан |
20 |
9,46 |
13.56 |
|
изогептан |
14,42 |
6,60 |
10,42 |
|
пентан |
9,46 |
0,00 |
0 |
|
изодекан |
0 |
0,00 |
0 |
|
изогексан |
0,0 |
23,57 |
20,02 |
|
гексан |
40 |
7,26 |
35,054 |
|
гептан |
20 |
3,99 |
15,054 |
|
изооктан |
3,99 |
8,00 |
8,660 |
|
октан |
8 |
0,00 |
7,999 |
|
нонан |
0 |
0,00 |
0 |
|
декан |
0 |
0,00 |
0 |
|
ундекан |
0 |
0,00 |
0 |
Результат расчета по модели (4)–(6) представлены трехмерным графиком на рисунке. По оси x – название компонент состава, по оси y – количество компоненты в составе и по оси z – время расчета (рисунок).
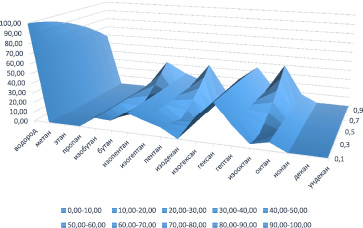
Результаты расчета процесса гидрокрекинга н-парафинов фракции
Алгоритм расчета модели (4)–(6) заключается в следующем:
1. Задать начальное время работы модели t = 0, ?t = 0,1.
2. Распределить исходный состав по трем категориям: изопарафины, нормальные парафины и водород.
3. Для каждой категории подобрать функцию плотности распределения вероятностей.
4. Используя значения параметров процесса (констант скоростей). компонентов вектора начального состава смеси, рассчитать результаты процесса.
5. Рассчитать значение октанового числа.
6. t = t + ?t и перейти к шагу 2.
7. Если значение октанового числа на каком-то шаге моделирования уменьшится – прекратить расчет
8. Если значение октанового числа не увеличивается в сторону заданного предела – прекратить расчет. Проанализировать результаты. Изменить значения параметров, связанные с технологическими показателями процесса. Вновь запустить расчет.
9. Если 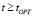 – прекратить расчет, вывести результат расчетов, проанализировать результаты, изменить значения параметров, связанные с технологическими показателями процесса. Вновь запустить расчет.
– прекратить расчет, вывести результат расчетов, проанализировать результаты, изменить значения параметров, связанные с технологическими показателями процесса. Вновь запустить расчет.
Адекватность модели для данного примера проверялась с помощью критерия Фишера:
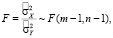
где 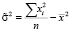 – выборочная дисперсия;
– выборочная дисперсия; 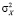 – продукты (эксперимент),
– продукты (эксперимент), 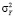 – продукты (расчет).
– продукты (расчет).
Результат проверки на адекватность: 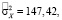
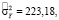 F = 0,83.
F = 0,83.
Для выяснения значимости проверки адекватности критерия Фишера использовали шкалу Чеддока:
1) 0,1 < F < 0,3: слабая;
2) 0,3 < F < 0,5: умеренная;
3) 0,5 < F < 0,7: заметная;
4) 0,7 < F < 0,9: высокая;
5) 0,9 < F < 1: очень высокая.
Критерий Фишера показал высокую и прямую связь между данными: «продукты (эксперимент)» и «продукты (расчет)», так как значение коэффициента F входит в интервал (0,7; 0,9).
Выводы
Таким образом, разработана математическая модель кинетики реакций процесса гидрокрекинга смеси н-парафинов. Кинетическая модель, представленная в форме интегро-дифференциальных уравнений, позволяет в значительной мере сократить математическое описание процесса в реакторе. Алгоритм решения дифференциальных уравнений в трехмерном пространстве позволил визуализировать результаты процесса. Расчеты на модельной смеси и сравнение результатов расчета с результатами лабораторного эксперимента показали, что на 9-м шаге моделирования при заданных параметрах удается достичь значения октанового числа, равного 70. Дальнейшая оптимизация возможна при условии правильно подобранных технологических параметров. Показана адекватность представленной математической модели при заданных начальных условиях.
Работа выполнялась в рамках гранта РФФИ 18-47-860003 р_а «Математическое моделирование процессов нефтепереработки и нефтехимии на основе динамических моделей в терминах смесей непрерывного состава».
Библиографическая ссылка
Микшина В.С., Касаткин В.В., Назина Н.Б., Погореловский М.А. МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ УПРАВЛЕНИЯ ПРОЦЕССАМИ НЕФТЕПЕРЕРАБОТКИ НА ОСНОВЕ НЕПРЕРЫВНОГО ПОДХОДА // Современные наукоемкие технологии. 2019. № 12-1. С. 84-88;URL: https://top-technologies.ru/ru/article/view?id=37838 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.37838



