В современном машиностроительном производстве вопросы комплексной автоматизации технологических процессов невозможно решить в полной мере, если для технологических установок не обеспечены такие технические параметры, как надёжность, долговечность и производительность. Перечисленные выше параметры в значительной степени определяются динамическими качествами системы гидроприводов отдельных механизмов каждого технологического узла металлорежущих станков. Улучшения технико-экономических показателей и расширения функциональных возможностей гидропривода на современном этапе развития можно добиться в основном за счет улучшения систем его управления. Важнейшим требованием к замкнутым системам управления является возможность гибкой настройки их параметров, а также быстрого программирования и перепрограммирования алгоритмов управления гидроприводов в зависимости от конкретных эксплуатационных условий.
Такой подход обеспечивает широкие возможности качественного перевооружения промышленности, быстрой переналадки производства при высоком уровне автоматизации, повышает производительность труда за счет снижения продолжительности производственного цикла, снижает потребность в квалифицированных рабочих вследствие сокращения ручных операций, то есть ориентирован на комплексную автоматизацию единичного и серийного производства при минимальном участии человека в этом процессе.
Технический уровень и эксплуатационные показатели современной автоматизированной машины однозначно определяются параметрами и характеристиками его привода, который является энергетической основой всех технологических и производственных процессов.
Наиболее полно эти требования можно выполнить только за счет применения автоматических систем стабилизации сил резания, т.е. поддерживать силы резания на постоянном уровне при любых проявлениях возмущающего воздействия, за счет которого одновременно повышается надежность функционирования оборудования станков и инструментов [1, 2].
К известным возмущающим воздействиям сил резания при любом виде механической обработки в ходе изготовления детали относятся те возмущения, которые постоянно присутствуют по следующим причинам: изменения припуска и твердости материала по длине обработки детали, износа инструмента, температурных деформаций, что в конечном итоге технологическая система подвергается различным упругим деформациям, приводящим к появлению погрешностей обработки детали.
Возникает необходимость в применении к объекту регулирования, в данном случае автоматического регулятора, состоящая из следующих элементов: информационного устройства – датчика, измеряющего силу резания и преобразующего ее в электрический сигнал, сравнивающего элемента – сумматора, на вход которого поступают сигнал с выхода датчика и задающий сигнал с выхода программного устройства, выходной сигнал сумматора, являющийся сигналом рассогласования, усиливается по мощности усилителем, а также регулятора, оказывающего воздействие на объект регулирования, в данном случае – гидросуппорт подачи инструмента.
В связи с этим определенный интерес представляет теоретическое исследование объекта управления, имеющего безынерционный регулятор расхода, поступающего в рабочую полость цилиндра гидросуппорта.
При построении систем автоматического управления нагрузка на валу рабочего органа, как правило, считается заданной (расчетной) и постоянной. Пределы ее изменения определяются параметрами и производственными характеристиками самой машины. Для обеспечения надёжности и долговечности машины максимальная нагрузка должна быть ограничена допустимыми значениями момента, усилия и ускорения, развиваемой валом рабочего органа.
В замкнутой системе автоматического управления в формировании управляющего воздействия участвуют две информации: заданная и текущая. Текущая информация измеряется с помощью датчика регулируемого параметра и преобразуется им в электрический сигнал. Этот сигнал подается на вход управляющего устройства в качестве сигнала обратной связи.
Для исследования процессов, происходящих в системах автоматического управления, необходимо написать общее дифференциальное уравнение всей системы. При прочих равных условиях составление адекватного уравнения возможно только в том случае, если установлены взаимосвязи между входными и выходными параметрами каждого из элементов системы как в статическом, так и в динамическом режиме.
Дифференциальное уравнение объекта регулирования, работающего с малыми отклонениями от рабочей точки, целесообразно представлять от полных величин переменных S, Q, к отклонениям ΔS, ΔQ.
Тогда уравнение объекта гидросуппорта представляется в виде
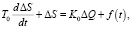(1)
где Т0 – постоянная времени, характеризующая инерционность гидросуппорта; К0 = 1/F – коэффициент усиления объекта; f(t) – возмущающее воздействие.
Уравнение безынерционного регулятора расхода:
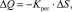(2)
где Kрег – коэффициент усиления регулятора, равен произведению всех коэффициентов усиления его элементов.
Тогда общее дифференциальное уравнение автоматической системы можно записать в виде
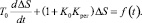(3)
Как известно, процесс регулирования подачи инструмента состоит из двух частей: переходного процесса ΔSпер(t) и установившегося процесса ΔSуст(t).
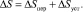(4)
Переходной процесс математически является общим решением дифференциального уравнения (2) при f(t) = 0.
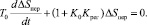(5)
Характеристическое уравнение для (5) имеет вид: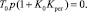 
Его корень равен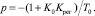 
С учетом полученного корня характеристического уравнения переходная составляющая общего интеграла, как решение однородного уравнения равна [2–4]:
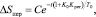(6)
где С – произвольная постоянная, определяемая из заданных начальных условий.
Кривая переходного процесса (5) для положительного значения С > 0 показана на рис. 1.
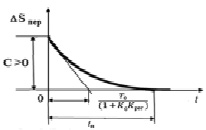
Рис. 1. График переходного процесса при С > 0 объекта с регулятором
Для сравнительной оценки переходных процессов гидросуппорта с безынерционным регулятором и без него, необходимо решить дифференциальное уравнение объекта без регулятора.
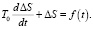(7)
Его характеристическое уравнение будет
(8)
Переходной процесс объекта без регулятора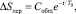 
где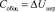 
.
Кривая переходного процесса объекта без регулятора представлена на рис. 2.
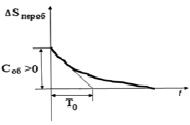
Рис. 2. График переходного процесса объекта без регулятора
Сравнивая переходные процессы объекта с регулятором (рис. 1) и без него (рис. 2), видим, что: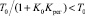 
.
Отсюда вывод, что длительность переходного процесса объекта с безынерционным регулятором в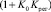 
раз меньше, чем у объекта без регулятора, то есть
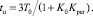(9)
Установившийся процесс зависит, как было отмечено выше, от конкретного значения возмущающегося воздействия f (t).
Рассмотрим случай мгновенного скачкообразного воздействия на систему f (t) = const = f0. График воздействия представлен на рис. 3.
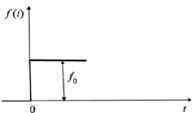
Рис. 3. Возмущающее воздействие на объект в виде f0 = const
В этом случае установившееся значение регулируемой величины определяется из уравнения (3), когда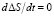 
[2, 3]:
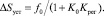(10)
Из формулы (10) видно, что для уменьшения автоматической ошибки регулирования надо брать по возможности большее значение коэффициента регулирования.
Объект без регулятора будет иметь установившееся значение:
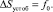(11)
Сравнение формул (10) и (11) позволяет сделать вывод, что присоединение к объекту безынерционного регулятора уменьшает статическую ошибку в (1 + K0Kрег) раз.
Обычно по технологическим требованиям на проектирование автоматических систем всегда задается наибольшая возможная статическая ошибка регулирования при реальных возможных значениях f0, и из этого условия определяется коэффициент усиления Kрег.
Полное решение дифференциального уравнения автоматической системы – объект + регулятор складывается из общего и частного решений уравнения (3) [4, 5]:
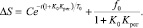(12)
Постоянное интегрирование находится из начальных условий: при t = 0; ?S = 0.
Из (12) находим: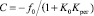 
.
Таким образом, процесс регулирования будет осуществляться по следующему закону:
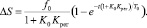(13)
Объект без регулятора при тех же начальных условий будет иметь следующее решение:
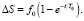(14)
На рис. 4 показаны переходные процессы гидросуппорта с регулятором и без него, наглядно демонстрирующие эффективность объекта с регулятором.
Следует отметить, что объекты с безынерционным регулятором и без него работают устойчиво, то есть переходные процессы являются затухающими, поскольку в левой части дифференциального уравнения коэффициенты при переменных постоянны и имеют положительный знак, а также корни характеристического уравнения являются действительными и отрицательными.
Более подробно исследуем устойчивость системы регулирования.
Система регулирования с затухающим процессом (рис. 4) называется устойчивой и в данном случае система регулирования будет устойчивой при любых значениях параметров объекта и регулятора, так как показатель степени е является отрицательным при любых значениях коэффициентов усиления системы (положительные числа).
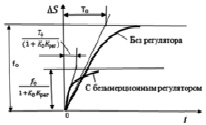
Рис. 4. Переходные процессы объекта с безынерционным регулятором и без него
Следует отметить, что правильное присоединение регулятора к объекту означает правые части уравнения регулятора и регулирующего объекта имели бы противоположные знаки при всех положительных коэффициентах обоих уравнений. Физически это значит, что регулятор при этом дает такое направление воздействия на объект, которое действительно направлено на уничтожение создавшегося отклонения регулируемой величины, или можно сказать иначе, что правильное присоединение регулятора в общем случае (при любых знаках коэффициентов в уравнении объекта) будут такими, которые делают положительными все коэффициенты левой части уравнения динамики системы регулирования в целом.
Рассмотрим случай, когда может получиться неустойчивая система с безынерционным регулятором – это случай регулирования неустойчивого объекта
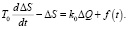(15)
Тогда уравнение системы будет
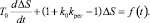(16)
Корень характеристического уравнения при этом
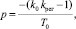(17)
и система будет устойчивой только в случае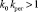 
.
Следовательно, с помощью безынерционного автоматического регулятора неустойчивый объект можно сделать устойчивым.
Выводы
1. Рассмотрены общее дифференциальное уравнение автоматической системы и дифференциальное уравнение объекта без регулятора.
2. Показано, что длительность переходного процесса объекта с безынерционным регулятором в (1 + K0Kр) раз меньше по сравнению, когда объект без регулятора, что наглядно видно из графиков (рис. 4).
3. На рис. 4 показаны переходные процессы гидросуппорта с регулятором и без него, наглядно демонстрирующие эффективность объекта с регулятором. Объекты с безынерционным регулятором и без него работают устойчиво, то есть переходные процессы являются затухающими.
Библиографическая ссылка
Кадыров И.Ш., Давлятов У.Р., Турусбеков Б.С. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГИДРОСУППОРТА СТАНКА С БЕЗЫНЕРЦИОННЫМ РЕГУЛЯТОРОМ // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 63-67;URL: https://top-technologies.ru/ru/article/view?id=37834 (дата обращения: 19.04.2024).