Продолжительный опыт эксплуатации отечественной ракетно-космической техники (РКТ) свидетельствует о наличии проблемы нарушения герметичности её элементов на различных этапах жизненного цикла [1, 2].
В настоящее время орбитальные средства оснащаются системами контроля герметичности, однако ни в одной из данных систем не предусмотрена функция определения места негерметичности в целях её оперативной ликвидации [3].
Ключевым вопросом в рамках данной проблемы является выбор методов и средств локализации течей, применимых в условиях вакуума на этапе наземных испытаний и при штатной эксплуатации.
Цель исследования: изучение взаимодействия дисперсного индикатора – мелкодисперсного вещества – с локальной негерметичностью при больших числах Кнудсена для решения задач локализации течей герметичных отсеков ракетно-космической техники в условиях вакуума.
Материалы и методы исследования
Одним из реализуемых на практике методов контроля герметичности герметичных отсеков (ГО) РКТ в условиях вакуума является метод с использованием дисперсного индикатора – мелкодисперсного вещества.
При взаимодействии истекающего через течь газа с пробным мелкодисперсным веществом нарушается поле его распределения, что может регистрироваться соответствующими средствами [4]. В настоящей работе рассматривается связанное мелкодисперсное вещество – волокнистый чувствительный элемент (ВЧЭ). ВЧЭ представляет собой пучок органических волокон, способных реагировать на истекающий через локальную негерметичность поток газа. Процессы взаимодействия ВЧЭ и несвязанного мелкодисперсного вещества с течью происходят по одним и тем же закономерностям.
При больших числах Кнудсена (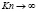
) реализуется свободномолекулярное течение и в общем случае описывается уравнениями Больцмана. Рассмотрим стационарное истечение газа из прямоугольного отверстия со сторонами 2a ≥ 2b в вакуум, когда размеры отверстия много меньше размера емкости и длин свободных пробегов молекул и распределение молекул по скоростям описывается максвелловской функцией.
После интегрирования функции распределения по пространству скоростей газодинамические параметры в безразмерном виде вдоль оси симметрии с началом координат в центре отверстия описываются следующими соотношениями [5]:
плотность
,
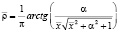плотность тока
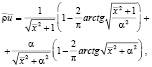(1)
скорость
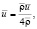
скоростной напор
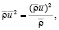
где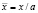 
, α = b/a.
Обезразмеривание осуществлялось следующим образом:
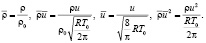
На рис. 1 представлены распределения газодинамических параметров вдоль оси симметрии для отверстия квадратного сечения α = 1.
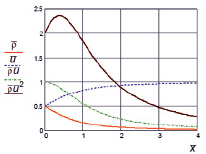
Рис. 1. Распределения газодинамических параметров вдоль оси симметрии для отверстия квадратного сечения α = 1
Построим математическую модель взаимодействия молекулярного пучка с дисперсным индикатором. Схема задачи показана на рис. 2.
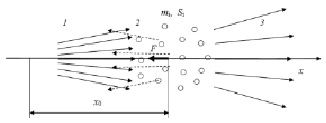
Рис. 2. Схема задачи построения математической модели взаимодействия молекулярного пучка с дисперсным индикатором
Пусть дисперсный индикатор массой mi и площадью миделя Si в начальный момент времени находится на расстоянии x0 от начала координат (центра отверстия) в вакууме. В момент времени t > 0 вследствие возникновения негерметичности на него начинает воздействовать молекулярный поток с параметрами (1), рассчитанными при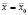 
. При этом часть молекул, пересекающих сечение с площадью миделя индикатора отразится с ненулевой осевой проекцией скорости в обратном направлении, а некоторый поток молекул пролетит насквозь.
Составим уравнение сохранения количества движения молекулярного потока и дисперсного индикатора:
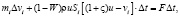(2)
где mi, Si – масса индикатора и площадь его миделя; ?vi – изменение скорости индикатора за элементарный промежуток времени ?t; F – внешняя сила, действующая на индикатор (например, сила тяжести или сила сопротивления при закреплении); ς – коэффициент восстановления при ударе молекул по поверхности дисперсной частицы; W – вероятность того, что молекула, траектория которой пересекает дисперсный индикатор, не отразится, а пролетит его насквозь.
Величина W называется вероятностью прохождения или коэффициентом Клаузинга. Для простых геометрических форм, таких как цилиндрический канал, диффузор, конфузор и др. коэффициент Клаузинга может быть определен теоретически [5]. Для сложных геометрических форм и дисперсных образований, к которым относится рассматриваемый индикатор, W целесообразно определять экспериментально.
Разделим (2) на ?t и устремим к нулю ?t → 0, получим дифференциальное уравнение
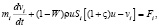(3)
позволяющее совместно с (1) описать динамику взаимодействия дисперсного индикатора с молекулярным потоком.
Рассмотрим задачу о взаимодействии молекулярного потока, истекающего из негерметичности с координатами (x0, 0) с дисперсным индикатором, подвешенным на нити с распределенной нагрузкой q = mg (m – масса единицы длины нити, g – ускорение свободного падения) с начальным положением (0, 0) (рис. 3).
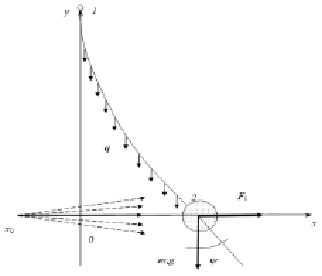
Рис. 3. Схема задачи взаимодействия молекулярного потока, истекающего из негерметичности, с дисперсным индикатором, подвешенным на нити
Уравнения равновесия нити в плоскости имеют вид [6]:
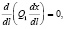(4)
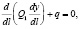
где L – длина нити, Q1 – сила ее натяжения, q = mg – распределенная нагрузка от веса нити.
Перейдем к безразмерным переменным de = dl/l,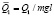 
, 
, 
, 
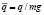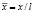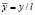имеем
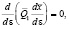(5)
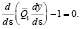
Интегрируя (5) и опуская промежуточные выкладки [6], получим уравнение формы нити:
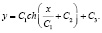(6)
Для определения неизвестных C1, C2 и C3 необходимы дополнительные условия. Таковыми в соответствии с условиями задачи являются:
координата узла подвеса
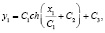(7)
длина нити
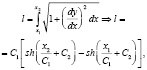
натяжение нити в узле подвеса
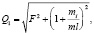(8)
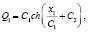
условие равновесия относительно узла подвеса
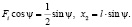(9)
Система (6)–(9) совместно с (3) дает решение поставленной задачи.
Теоретические исследования, проведенные с использованием современных высокоэффективных численных методов, показывают достаточно высокую эффективность рассматриваемого метода контроля герметичности. Однако некоторые допущения, положенные в основу разработанных математических моделей, требовали экспериментального подтверждения полученных результатов по адекватности реальным физическим процессам.
Результаты исследования и их обсуждение
В целях проведения экспериментальных исследований создан специальный стенд на базе стационарной вакуумной установки СМ 297М, дополнительно оборудованной электромеханическим манипулятором МЭМ-5С с синхронно следящей связью и системой управляющей и контрольно-измерительной аппаратуры.
Для проведения экспериментальных исследований в барокамеру установки СМ 297М помещался имитатор ГО с течью. На поперечную балку, расположенную внутри барокамеры, подвешивалась гибкая лавсановая нить длиной L = 0,57 м и погонной массой m = 30 мг с закреплённым на ней ВЧЭ. Барокамера откачивалась до давления (1,0…1,2)·10-5 мм рт. ст. В процессе проведения эксперимента проводился замер суммарного натекания в барокамеру, по величине которого были рассчитаны количественные характеристики течи. Одновременно с помощью катетометра КМ-8 через смотровое окно барокамеры производилось визуальное наблюдение за поведением ВЧЭ и осуществлялись замеры отклонения элемента от контрольной точки. Все данные и результаты документировались, после чего изменялись количественные характеристики течи путём изменения давления на входе в имитатор герметичного отсека, и измерения повторялись. В последующем гибкая нить с элементом удалялась с помощью манипулятора МЭМ-5С от течи в горизонтальном и вертикальном направлениях на фиксированное расстояние и производились вышеперечисленные замеры количественных характеристик течи и отклонения волокнистого чувствительного элемента.
Результаты исследования взаимодействия мелкодисперсного вещества с локальной негерметичностью при больших числах Кнудсена представлены на рис. 4.
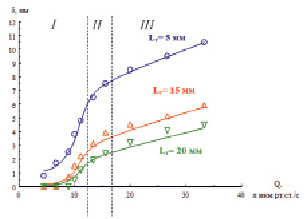
Рис. 4. Зависимость отклонения ВЧЭ от количественных характеристик течи
На рис. 4 фигурами (кружками и треугольниками) представлены результаты опытных замеров. Сплошными линиями показаны результаты теоретических расчетов. Там же показано, что характер изменения зависимости отклонения ВЧЭ от количественных характеристик течи различен для трёх условных областей диапазонов значений. Это связано с конкретными условиями проведения экспериментальных исследований, а именно с вариантом размещения и крепления дисперсного индикатора.
Для диапазона количественных характеристик течей (4,45 ≤ Q ≤ 11,11 л мкм рт. ст/с), лежащих в области I, нить можно представить в виде балки с односторонней заделкой, которая при взаимодействии молекулярного пучка с дисперсным индикатором изгибается на расстояния, соизмеримые с её поперечным размером. В этом случае необходимо учитывать влияние сил упругости, возникающих при изгибе нити, на процесс отклонения индикатора от контрольной точки.
Для диапазона количественных характеристик течей (Q ≥ 13,33 л мкм рт. ст/с), лежащих в области III нить с ВЧЭ представляется в виде абсолютно гибкого маятника и отклоняется на расстояния, несоизмеримо большие, чем её поперечные размеры. В этом случае действие сил тяжести превосходит действие сил упругости и, соответственно, изменение зависимости отклонения ВЧЭ от количественных характеристик течей имеет иной характер.
Существует также некая промежуточная область значений (область II) (11,11 ≤ Q ≤ 13,33 л мкм рт. ст/с), при которой происходит процесс перехода от одной модели к другой.
В связи с тем, что при моделировании процесса взаимодействия молекулярного пучка с ВЧЭ были применены две различные модели, для построения графических зависимостей был использован робастный метод сглаживания данных (робастная локально-взвешенная регрессия), позволяющий обеспечить более полную картину связи между переменными Q и δ.
Выводы
1. Исследование взаимодействия ВЧЭ с локальной негерметичностью при больших числах Кнудсена показало возможность его применения в целях локализации течей ГО РКТ.
2. Полученные результаты могут быть использованы в существующих системах контроля герметичности ГО РКТ для обнаружения мест негерметичностей в условиях вакуума при наземных испытаниях и штатной эксплуатации.
Библиографическая ссылка
Добролюбов А.Н., Лебедев А.С. ВЗАИМОДЕЙСТВИЕ МЕЛКОДИСПЕРСНОГО ВЕЩЕСТВА С ЛОКАЛЬНОЙ НЕГЕРМЕТИЧНОСТЬЮ ПРИ БОЛЬШИХ ЧИСЛАХ КНУДСЕНА // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 58-62;URL: https://top-technologies.ru/ru/article/view?id=37833 (дата обращения: 19.04.2024).