В период второй мировой войны в рамках научного направления «Исследование операций» [1] был сформирован класс задач распределения ресурсов. Тогда термин «Задача распределения ресурсов (ЗРР)» носил военный оттенок (выработка группами ученых разных специальностей рекомендаций по рациональным способам применения боевых и обеспечивающих средств). В послевоенный период ЗРР стали широко использоваться при обосновании решений в промышленности, аграрных отраслях, банковской и транспортной сферах и т.д. В обобщенном виде ЗРР формулируется следующим образом: имеется ограниченное количество ресурсов, недостаточное для выполнения всех задач наилучшим образом, необходимо распределить ресурсы так, чтобы достичь наибольшего эффекта. В литературе по анализу современного процесса цифровизации деятельности органов управления различных организационно-технических систем (ОТС) отмечается [2–4], что вследствие использования промышленного интернета вещей (IoT), больших данных (big data) и искусственного интеллекта (AI) возникли проблемы, обусловленные разнообразием, немасштабируемостью и недостоверностью первичной информации. В состав ОТС в качестве основных подсистем входят: исполнительная, управляющая и информационная. Специальное математическое обеспечение (СМО) систем управления ОТС включает комплекс программ, предназначенных для оптимизации выполнения целевых задач; реализация данного комплекса требует значительных вычислительных затрат [2, 5, 6]. Для учета точностных характеристик системы информационного обеспечения и доработки данного комплекса программ необходимо решить новую научную задачу – установить связь между ошибками в исходных данных и результатом решения классических ЗРР и, далее, обосновать альтернативные (по отношению к оптимизационным) алгоритмы распределения ресурсов.
Традиционно при разработке капиталоёмких проектов крупномасштабных ОТС используются алгоритмы решения задач двух типов [1, 7, 8]:
- оптимизационной задачи с критерием минимума продолжительности (tцз) всей операции по целевому обслуживанию соответствующих объектов при заданном лимите средств на достижение цели (ОЗ-I);
- оптимизационной задачи с критерием минимума расхода средств (rцз) на достижение цели при ограничении на продолжительность tцз операции (ОЗ-II).
Рассмотрим два существенных аспекта сформулированных задач предварительного или оперативного планирования распределения ресурсов:
1) введение дополнительных средств в операцию не должно быть единственным способом увеличения вероятности достижения требуемого эффекта;
2) процессы выполнения плановых задач в различных сферах функционирования ОТС имеют стохастический характер (вследствие воздействий техногенных и природных факторов, которые можно только минимизировать, но не аннулировать).
Учет перечисленных аспектов позволяет переформулировать ОЗ-II в задачу с критерием максимума вероятности (Pцз) достижения требуемого эффекта [9, 10], например, максимума вероятности обслуживания числа nоб объектов не менее заданного Nтр: Pцз = P(nоб > Nтр) при tцз < tтр и rцз < R.
Результаты решения ОЗ-I и ОЗ-II (планы назначений) будем обозначать через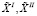 
соответственно. Результаты решения альтернативной задачи распределения ресурсов (ОЗ-III) обозначим через 
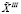. Практика показывает, что для решения ОЦ-I и ОЦ-II необходимы значительные затраты времени [11, 12]. Это связано с тем, что и при проектировании, и в ходе оперативного управления необходимо учитывать множество ограничений как на величины tцз, Pцз, так и на способы функционирования ОТС, которые придают ОЦ-I и ОЦ-II статус динамических нелинейных задач. Кроме того, очевидно, на любой стадии жизненного цикла ОТС исходная информация известна с определенными погрешностями и имеют место погрешности самих численных алгоритмов. Следствием данного обстоятельства может быть принятие ошибочного плана лицом, принимающим решение (ЛПР). Исходные данные должны корректироваться как в заранее предусмотренные сроки, так и вследствие неожиданных обстоятельств, из-за смены концепций, при выявлении необоснованных допущений. Неточность исходных данных может быть обусловлена волатильностью результатов вспомогательно-обеспечивающих расчетов (например, определения координат объектов, корректирования оценочных работ, проведения внезапных экспертиз), ошибками операторов нанесения электронных маркировок при создании национальных цифровых платформ для сбора различной информации и т.д. [13].
Таким образом, требуется разработать алгоритмы распределения ресурсов, альтернативные по отношению к оптимизационным, но обеспечивающие определенную вероятностную гарантию выполнения целевой задачи, поставленной перед ОТС.
Материалы и методы исследования
Проведем оценивание вариантов вероятностного выбора плана назначений. Обозначим через ts продолжительность выполнения целевой задачи при распределении ресурсов по s-му варианту. Этот частный показатель эффективности является функцией элементов временной и вероятностной матриц – продолжительностей tij единичного взаимодействия i-го ресурса с j-м объектом и вероятностей vij успешных единичных взаимодействий. Число вариантов S определяется методами комбинаторики, каждый вариант формируется соответствующим программным генератором.
В рассматриваемом варианте распределения ресурсов продолжительность tцз выполнения целевой задачи является смешанной случайной величиной, а ее возможные значения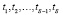 
распределены в некотором интервале 
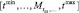. Ориентировочное суждение о целесообразности решения ОЦ-I принимается по величине 
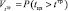, вычисляемой по формуле [9, 10]:
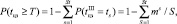
где ST – номер интервала, соответствующего неравенству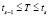 
, mS – суммарное количество планов, при которых величина tцз принимает значение tS.
Для учета физической невозможности для некоторого i-го ресурса осуществить обслуживание j-го объекта соответствующим элементам в матрице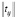 
присваиваются искусственно завышенные значения. После составления временной матрицы осуществляется обращение к генератору планов, далее – количественное оценивание скрытности использования конкретного закона распределения номеров генерируемых вариантов и вычисление величин 
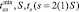, mS и 
.
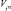Обозначим через Ps вероятность выполнения целевой задачи при распределении ресурсов по s-му варианту. Введем в рассмотрение величину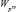 
= P(Pц.з < Pтр), где Pц.з. – вероятность выполнения целевой задачи при реализации стохастического способа распределения ресурсов, Pтр. – требуемое (указанное в руководящих документах) значение этой вероятности. В рассматриваемом варианте (вероятностный способ) вероятность Pц.з. является смешанной случайной величиной, а ее возможные значения 
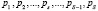распределены в соответствующем интервале 
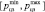. Алгоритм вычисления 
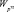аналогичен алгоритму расчета показателя 
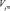: составление вероятностной матрицы, обращение к генератору планов, далее – количественное оценивание скрытности использования конкретного закона распределения номеров генерируемых вариантов и вычисление величин Pц.з, mS и 
.
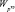Из вышеизложенного следует, что степень надежности выполнения целевой задачи на этапах проектирования ОТС и планирования применения ОТС необходимо оценивать по двум вероятностным показателям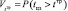 
и 
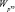= P(Pц.з < Pтр), где tтр и Pтр – задаваемые заказчиком требования к результатам выполнения целевой задачи. Показатель 
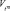характеризует оперативность решения целевой задачи, показатель 
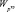характеризует результативность функционирования ОТС.
Рассмотрим процедуру получения плана назначений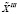 
, разработанную авторами. В её состав должны входить два следующих алгоритма – алгоритм выявления пар (i×j)з , i = 1(1)M, j = 1(1)N, для которых вследствие тех или иных ограничений невозможны единичные акты обслуживания, и алгоритм генерации всевозможных вариантов обслуживания. Процедура получения плана 
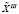заключается в поэтапном обращении к генератору вариантов, проверке на каждом h шаге факта отсутствия в полученном плане комбинаций (i×j)з и отбраковке плана 
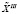з, содержащего такие пары. При первом появлении плана 
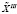h, не имеющего в своем составе ни одной пары (i×j)з, описанный процесс останавливается. Предлагается использовать два типа генераторов вариантов обслуживания 
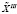h, h = 1(1)K(M,N).
Генератор первого типа позволяет последовательно получить весь набор всевозможных распределений М средств по N объектам. При конструировании этого генератора была использована идея функционирования спидометра с N дисками и М ячейками для цифр на каждом диске. Пусть первый диск – аналог первого столбца в матрице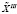 
[M,N] вращается с некоторой скоростью z, второй – со скоростью z/M2 и т.д., тогда после совершения N-м диском полного оборота наш «спидометр» выработает МN вариантов матриц 
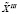h, h = 1(1)K(M,N). Однако при непосредственной реализации такой идеи возникает необходимость организации в программе N циклов или накопления в N ячейках чисел от 1 в первой ячейке до МN в N-й ячейке, что может привести к сбоям при суммировании очень малых чисел. Поэтому программа должна предусматривать стирание на каждом шаге всех ранее полученных вариантов. Например, при М = 3 и N = 4 вариант «в» следует из варианта «б» и не требует запоминания варианта «а» (рисунок).
Пример удаления избыточных вариантов
Составным элементом генератора второго типа является датчик случайных чисел ? (распределенных равномерно на интервале (0,1] либо по другому вероятностному закону). Обозначим через ? номер строки, в котором размещена единица в произвольном столбце матрицы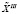 
(остальные элементы равны нулю). Последовательно обращаясь к датчику случайных чисел (ДСЧ), будем определять величины ? как ? = ?[M??] + 1. Очевидно, минимальное число обращений к ДСЧ равно N. При совпадении очередного значения ? с ранее полученным значением организуется новое обращение к ДСЧ и т.д.
Заметим, что при необходимости учесть наличие ограничений на число объектов, обслуживаемых одним средством, в генераторах обоих типов организуется программная сортировка: последовательно находятся суммы ?i, единиц в строках и для всех строк проверяется выполнение неравенства α ≤ ?i ≤ β. Заметим также, что генератор первого типа может использоваться (в случае небольших размерностей) для решения оптимизационных распределительных задач методом слепого перебора, а также для определения примерного вида целевой функции.
Рандомизация для генератора первого типа заключается в дополнительном «ослучаивании» – отборе самих получаемых вариантов с помощью ДСЧ. Рандомизация для генератора второго типа обусловлена непосредственно предлагаемой технологией. В качестве достоинства разработанных генераторов, как уже отмечалось, следует указать сложность вычисления плана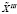 
[M,N] конкурентами, но степень уязвимости первой процедуры несколько выше, чем у второй.
Результаты исследования и их обсуждение
Проведем анализ целесообразности реализации вероятностного способа распределения ресурсов. В зависимости от предназначения ОТС, ситуационной осведомленности и от общей обстановки перед ЛПР может возникнуть необходимость решения следующих частных задач:
1. Распределение ресурсов по критерию max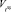 
при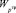 
> Wзкч (уровень Wзкч определяется заказчиком).
2. Распределение ресурсов по критерию min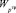 
при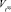 
> Vзкч (уровень Vзкч устанавливается заказчиком).
3. Распределение ресурсов по векторному критерию <max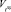 
, min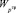 
> (соответствующие ограничения вводятся дополнительно, в зависимости от конкретной обстановки и организационных рисков). При этом классический субъективизм, присущий многокритериальным задачам [8, 14], в рассматриваемой задаче «усиливается», так как ЛПР должен не только обосновать уровень требований к Pц.з. и tц.з., но и сформировать, исходя из здравого смысла, приемлемый уровень гарантирующих вероятностных показателей Vзкч и Wзкч.
Обязательность выполнения более «жестких» требований к результативности и оперативности и, как следствие, к генерируемому плану распределения ресурсов (что обусловлено двумя процедурами рандомизации), является своеобразной платой за гарантию достижения целевого эффекта в условиях значительных затрат машинного времени на обработку большого объема данных.
Более упрощенные подходы к оцениванию целесообразности реализации вероятностного способа распределения ресурсов заключаются в следующем. Обозначим результат решения ОЦ–I через tImin (эта величина определяется планом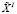 
), через 
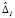– суммарную ошибку вычисления минимальной продолжительности выполнения задачи. Тогда при 
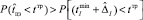решение ОЦ-I нецелесообразно. В соответствии с изложенной логикой решение оптимизационной задачи II типа нецелесообразно при 
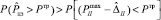, где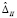 
– суммарная ошибка решения задачи по максимизации вероятности достижения цели, 
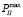– результат решения ОЦ-II (определяется планом 
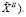Следует подчеркнуть, что при выборе закона распределения номеров вариантов (генерирования вариантов) необходимо руководствоваться требованием скрытия от конкурирующих структур замысла действий, что является необходимым условием в обстановке противоборства любого вида. Заметим, что указанное обстоятельство является еще одним аргументом в пользу вероятностного способа при выборе подходов к решению ЗРР. Невозможность априорного (путем решения «зеркальной» оптимизационной задачи) вычисления плана конкурентами (противником) обусловлена применением датчика случайных вариантов, при этом закон распределения номеров вариантов должен назначаться непосредственно перед началом планирования (применения).
Алгоритмы оценивания выигрыша от реализации ОЦ-I и ОЦ-II в детерминированной постановке приведены в работах [9, 10], при этом учитывается разброс значений элементов матрицы «времен» в широких пределах: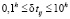 
, где h – условная единица измерения времени функционирования, обусловленный различия в масштабах, технологиях, степени противодействия, финансовом обеспечении ОТС различного предназначения.
Следует отметить, что в работах [7, 8, 15] при рассмотрении алгоритмов решения задач распределения ресурсов не учитывается связь между аргументами целевой функции (соответствующих, как правило, нижним уровням системы моделей) и вероятностью достижения цели. Наличие этой зависимости (например, между изменением математического ожидания целевого параметра и изменением среднеквадратического отклонения) связано с тем, что они определяются, возможно, одними и теми же эксплуатационно-техническими характеристиками (ЭТХ) и условиями функционирования ОТС. Следовательно, при определенных комбинациях увеличение математического ожидания приведет не к максимизации, а к уменьшению вероятности выполнения задачи.
Универсальных аналитических методик нахождения взаимосвязи вариаций ЭТХ, параметров обстановки, изменений математического ожидания и изменений среднеквадратического отклонения не существует, так как любой соответствующий алгоритм определяется не только законом распределения показателя результативности, но и иерархией параметров технических устройств и оборудования, конструктивной схемой инфраструктурных блоков, характеристиками уровней информационного контура ОТС. Перечисленные исходные данные всегда конкретны, «не вписываются» в общие описательные модели. Поэтому в интересах решения ОЗ-III необходимо реализовывать имитационные модели, в которых должно быть предусмотрено адаптированное обращение ЛПР к генератору вариантов распределения ресурсов. Далее по результатам моделирования составляются уравнения регрессии, связывающие рост (уменьшение) вероятности выполнения задачи с изменениями ЭТХ, динамикой обстановки, увеличением математического ожидания и изменением дисперсии.
Заключение
В статье предложен подход к обеспечению требуемой точности решения задач распределения ресурсов в условиях наличия ошибок в исходных данных и погрешностей вычислительных алгоритмов. В рамках теории эффективности разработанная методика относится к классу методик синтеза, учитывает погрешности численных алгоритмов и ошибки систем информационного обеспечения, является альтернативной по отношению к методикам классической оптимизации и обеспечивает гарантированное выполнение целевой задачи.
Анализ предметной области показывает, что ранее вопросы исследования целесообразности применения эвристических стохастических алгоритмов применительно к задачам распределения ресурсов не рассматривались [6, 8, 15]. Реализация разработанной методики в составе комплекса алгоритмов автоматизированных систем органов управления ОТС позволит при планировании распределения ресурсов обеспечить наращивание показателей ее эффективности за счет реконфигурации СМО ОТС.
Библиографическая ссылка
Волков В.Ф., Пономарев А.С. ИССЛЕДОВАНИЕ ЦЕЛЕСООБРАЗНОСТИ ПРИМЕНЕНИЯ СТОХАСТИЧЕСКИХ АЛГОРИТМОВ В ЗАДАЧАХ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 42-46;URL: https://top-technologies.ru/ru/article/view?id=37830 (дата обращения: 19.04.2024).