Добыча алмазов – одна из основных отраслей промышленности Республики Саха (Якутия). После аварии на руднике «Мир», восстанавливать который начнут только в 2024 г., объем добычи упал на 10–11 %. Поэтому все более привлекательными для промышленной разработки становятся россыпные месторождения. Среди россыпных месторождений наиболее часто встречается аллювиальный тип, развитый в малых и средних реках. Протяженность россыпей изменяется от километров до нескольких десятков километров, ширина – от десятков до сотен метров [1].
Территория Якутии составляет более трех миллионов квадратных километров, из них 28,5 % относятся к охраняемым территориям. Этому способствует низкая плотность населения – около 0,3 человека на квадратный километр. В Якутии разработана стройная система особо охраняемых природных территорий (ООПТ), включающая в себя природные парки, заповедники, заказники, ресурсные резерваты, охраняемые ландшафты и памятники природы, а также зеленые зоны селитебных мест [2]. Введена принципиально новая форма ООПТ – ресурсный резерват, содержащий в себе элементы четвертой-седьмой категорий охраняемых территорий Международного союза охраны природы. Введение резерватов продиктовано обширностью сети ООПТ, что затрагивает уклад жизни коренных народов. К ресурсным резерватам относятся зоны абсолютного покоя, священные места, зоны лицензионного изъятия ресурсов, зоны сезонного изъятия природных ресурсов, зоны традиционного природопользования, охраняемые ландшафты и памятники природы.
Структура ареалов играет важную роль в динамике численности и распространении популяций. Последствия хозяйственной деятельности человека могут привести к изменению размеров среды обитания биологических видов. В случае изменения размеров охраняемой части билокального ареала, остается важным вопрос сохранения численности популяции.
Существенной проблемой является рекультивация территорий и восстановление биоценозов на них после окончания промышленных разработок. В северных условиях эти процессы длятся десятилетиями, до сих пор слабо разработаны методы восстановления нарушенных земель. На них развиваются биоценозы, отличные от существовавших природных, что приводит к уменьшению ареалов охраняемых популяций и замене видов, как правило, на менее ценные и менее прихотливые к условиям обитания. В республике возникают новые крупные промышленные объекты, такие как международный газопровод «Сила Сибири», при создании которого на месторождении «Чаянда» построен большой газовый комплекс, и задачи сохранения и восстановления видов, подвергшихся техногенному воздействию, становятся все более актуальными и требующими новых подходов их решения. Использование математического моделирования может быть полезным в этой ситуации.
В 1950-х гг. была освоена промышленная разработка россыпи алмазов на трубках «Мир», «Айхал», «Удачная», что было вызвано природными и технологическими особенностями проведения работ в условиях вечной мерзлоты. В результате выработки имеющихся месторождений россыпная алмазодобыча в Якутии продвигается все дальше на север, за Полярный круг, при этом отчуждая территории ресурсных резерватов. Примером такого продвижения является Верхне-Мунское месторождение алмазов, которое находится на западе Якутии в 170 км от г. Удачный на территории ресурсного резервата «Муна». На данный момент разведаны четыре кимберлитовые трубки: «Заполярная», «Деймос», «Новинка», «Комсомольская-Магнитная». Верхне-Мунское месторождение будет приносить порядка 1,8 млн карат алмазов в год в течение более 20 лет. Продолжительные техногенные работы могут существенно повлиять на сохранение биологического разнообразия на местности. Уменьшение территории ресурсного резервата влияет на охраняемые популяции животных, к числу которых относятся популяции лося, дикого оленя, соболя и колонка.
Целью работы является оценка влияния горной добычи на плотности охраняемых популяций с помощью математического моделирования их динамики.
Материалы и методы исследования
Промышленное освоение территорий приводит к разбиению мест обитания популяций на части. Рассматривается случай образования билокального ареала. Обозначим через u и v плотности популяции на сохраняемой в естественном виде территории и на промышленно осваиваемой территории. Исследование проводится с помощь классических уравнений диффузии, понимаемой как распространение популяции по двумерному ареалу [3]. Правые части уравнений дополнены членами, описывающими кросс-диффузию [4] и обобщенный ресурс. Система уравнений имеет вид
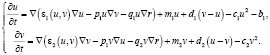
Расселение популяции по территории описывается диффузионными параметрами ε1(u, v), ε2(u, v) и p1, p2. Учет неоднородности среды обитания достигается функцией r(x, y). Скорости изменения плотностей популяции пропорциональны самим плотностям с коэффициентами пропорциональности m1, m2, члены d1, d2 описывают переходы особей из одной зоны ареала в другую, конкуренция за ресурс учитывается с помощью членов с c1, c2. Внешнее техногенное воздействие интерпретируется коэффициентом b1 [4–6].
Рассматривается ареал Ω = [0, l1]×[0, l2], на границах которого ставились условия, предполагающие, что особи популяции не покидают ареал, и что их численность на границах равна нулю. Отчуждение охраняемой территории описывалось изменением параметра l2.
Начальные распределения плотностей популяции могут быть заданы в виде поверхности на рассматриваемом ареале. В данной работе в качестве такой поверхности рассмотрено двумерное нормальное распределение. Функция ресурса также задается как поверхность, экстремальные значения которой являются благоприятными зонами ареала.
Для численного решения рассматриваемой задачи построен вычислительный алгоритм на основе метода расщепления по пространственным переменным, используя безусловно-устойчивые конечно-разностные схемы суммарной аппроксимации [7]. Вычислительный алгоритм реализован на языке программирования Python с использованием модифицированного метода прогонки и метода простых итераций [8, 9]. Разработан пакет программ для проведения вычислительных экспериментов при различных параметрах модели. Расчеты проводились до выхода на устойчивые стационарные распределения плотностей популяции [10].
Результаты исследования и их обсуждение
Численные расчеты показали, что уменьшение площади охраняемой территории вызывают меньший эффект, чем ожидалось. Это связано с тем, что в модели не учитывается изменение величины ресурса в промышленной зоне и коэффициенты перехода остаются постоянными. Если техногенное воздействие невелико, то плотности частей популяции стабилизируются на определенном, но меньшем начального уровне. Это можно объяснить наличием охраняемой части резервата. На рис. 1 приведены начальные и предельные величины плотностей обеих частей популяции при одинаковых площадях охраняемой и неохраняемой частей ареала. Предельные величины плотностей равны 0,5 для неохраняемой и 0,9 для охраняемой частей.
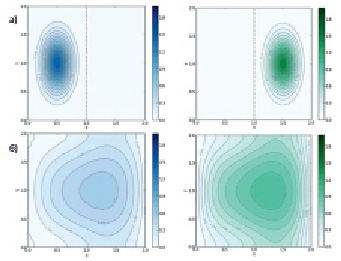
Рис. 1. Случай отношения частей ареала 1:1, (а) – начальные плотности u и v, t = 0, (б) – предельные плотности u и v, t = 15
При уменьшении охраняемой территории (соотношение частей ареала 5:3) предельные величины стабилизируются на более низком уровне – 0,4 и 0,8 соответственно. Дальнейшее уменьшение площади охраняемой части практически не приводит к изменению предельных плотностей обеих частей популяции (рис. 2). Этот эффект объясняется выбором значений параметров системы, при котором существует устойчивое стационарное состояние и наличием постоянного обмена особями между частями билокального ареала.
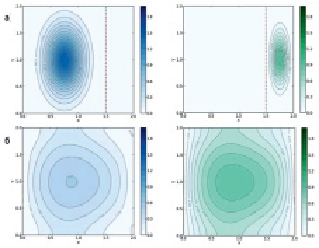
Рис. 2. Случай отношения частей ареала 3:1, (а) – начальные плотности u и v, t = 0, (б) – предельные плотности u и v, t = 15
В рассматриваемой модели имеется бифуркация типа «складка» [10], приводящая к вырождению всей популяции. Она возникает при больших техногенных нагрузках, т.е. при превышении критического значения бифуркационного параметра b1 в модели. Бифуркационный параметр выражается через коэффициенты функций f1 и f2. В случае незначительного превышения критической отметки (b1 = 0,39), в момент времени t = 3, при равных площадях частей ареала сохраняются ненулевые плотности охраняемой и неохраняемой частей популяции (рис. 3). Если при тех же значениях параметра системы уменьшить площадь охраняемой части ареала, то в тот же момент времени t = 3 неохраняемая часть популяции уже не существует (рис. 4).
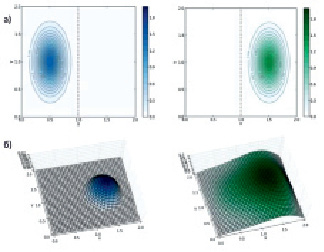
Рис. 3. Случай наличия в системе бифуркации при отношении частей ареала 1:1, (а) – исходные плотности u и v, t = 0, (б) – промежуточные плотности u и v, t = 3
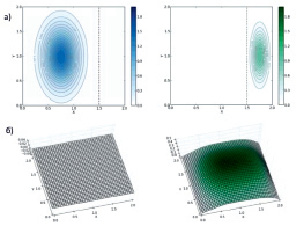
Рис. 4. Случай наличия в системе бифуркации при отношении частей ареала 3:1, (а) – исходные плотности u и v, t = 0, (б) – промежуточные плотности u и v, t = 3
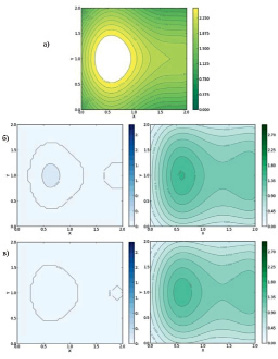
Рис. 5. Случай введения в систему функции ресурса, (а) – функция ресурса r(x, y), (б) – промежуточные плотности u и v, t = 10 при отношении частей ареала 1:1, (в) – промежуточные плотности u и v, t = 10 при отношении частей ареала 3:1
Учет неоднородности ареала достигается введением функции обобщенного ресурса в виде поверхности r(x, y). Пусть основной пищевой ресурс особей сосредоточен на неохраняемой части ареала (рис. 5, a). При большом техногенном воздействии и при равных площадях частей ареала это приводит к малой, но ненулевой плотности неохраняемой части популяции (рис. 5, б). Отчуждение части территории резервата под горные работы приводит к совсем уж малой, но ненулевой плотности неохраняемой части популяции (рис. 5, в).
Заключение
При решении задач экономики необходимо учитывать промышленное воздействие на природную среду и решать экологические проблемы одновременно с экономическими. Перевод части земель природного резервата под добычу полезных ископаемых не приводит к большим отрицательным воздействиям на охраняемые популяции только при правильной оценке природного потенциала. В случае присутствия экстремальных техногенных воздействий введение обобщенного ресурса позволяет сохранить присутствие популяции до определенного момента времени. Вид функции ресурса существенно влияет на формы предельных распределений обеих частей популяции.
Библиографическая ссылка
Васильев М.Д., Васильева Н.В., Матвеева О.И., Трофимцев Ю.И. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИИ ПРИ ПРОВЕДЕНИИ НА АРЕАЛЕ ПРОМЫШЛЕННЫХ РАБОТ // Современные наукоемкие технологии. 2019. № 12-1. С. 36-41;URL: https://top-technologies.ru/ru/article/view?id=37829 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.37829



