Для выделения целевых продуктов из зернистого материала используют различные конструкции аппаратов, однако наиболее эффективным из них является ситовое оборудование. Математическое моделирование происходящих при этом процессов является основой для технологического расчета ситовых классификаторов и оптимального управления процессами. В работе [1] и в ряде других работ этих авторов изучено движение частиц в колеблющейся среде, рассмотрены различные модели вибрационного движения и получены зависимости для средней скорости, скорости сегрегации. Следует также отметить, что работы этих авторов были одними из первых в области вибрационного разделения сыпучих сред. В работе [2] процесс разделения дисперсных сред на ситовых классификаторах рассмотрен как диффузионный процесс и изменение концентрации числа проходовых частиц по толщине слоя зернистого материала в зависимости от времени в направлении к вибрирующей поверхности изучено с позиций марковских процессов и описано уравнением Колмогорова – Фоккера – Планка (К. – Ф. – П.). В работах [3, 4] процесс выделения целевых продуктов на многокаскадных классификаторах также изучен с использованием теории случайных процессов, в частности в работе [4] для описания процесса перемещения частиц по поверхностям сит вследствие просеивания применяется теория Пуассоновских процессов. Изучению сегрегации частиц в виброожиженном слое на основе марковских цепей посвящена работа [5]. В работе [6] приведены основные принципы организации технологических процессов с управляемыми сегрегированными потоками, которые возникают при переработке зернистых материалов. Таким образом, для изучения процесса выделения целевых продуктов из зернистого материала можно использовать разные подходы, однако с учетом случайного характера процесса в целом наиболее предпочтительным является стохастический подход.
Целью работы является изучение процесса выделения целевых продуктов из зернистых материалов на ситовых классификаторах и построение его математической модели с использованием теории случайных процессов.
Математическое моделирование
Изучим процесс выделения целевых продуктов из зернистого материала на ситовых классификаторах с учетом стохастической природы подобных процессов. Диаметр частиц разделяемого зернистого материала рассматривается как одномерная случайная величина и для описания дисперсности зернистого материала задается плотность распределения частиц по размерам G(d). Тогда долю частиц выделяемого продукта в исходном материале можно найти по формуле
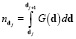 .
.
В качестве случайного процесса 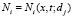 рассмотрим концентрацию числа частиц целевого продукта (1/м) размерами dj на поверхности i-го сита в точке x от начала координат в момент времени t. Тогда кинетические уравнения для определенного выше случайного процесса в общем виде можно записать [3, 7]:
рассмотрим концентрацию числа частиц целевого продукта (1/м) размерами dj на поверхности i-го сита в точке x от начала координат в момент времени t. Тогда кинетические уравнения для определенного выше случайного процесса в общем виде можно записать [3, 7]:
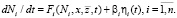
Здесь кинетические функции Fi характеризуют скорость просеивания на i-м ярусе, вектор 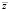 задает свойства материала, n – количество сит классификатора, ηi(t) – дельта-коррелированные во времени случайные функции, которые в каждый момент времени характеризуют отклонение концентрации числа частиц от ее среднего значения на i-м ярусе (белый шум), с характеристиками:
задает свойства материала, n – количество сит классификатора, ηi(t) – дельта-коррелированные во времени случайные функции, которые в каждый момент времени характеризуют отклонение концентрации числа частиц от ее среднего значения на i-м ярусе (белый шум), с характеристиками: 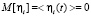 и
и 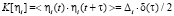 .
.
Здесь βi – интенсивность, 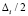 – спектральная плотность белого шума. Особенностью этих уравнений, которая позволяет назвать их стохастическими, является наличие воздействия в виде белого шума.
– спектральная плотность белого шума. Особенностью этих уравнений, которая позволяет назвать их стохастическими, является наличие воздействия в виде белого шума.
Число частиц выбранной фракции на поверхности i-го сита в любой момент времени 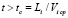 определяется по выражению
определяется по выражению
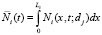 ,
,
где Li – длина сита, Vi cp – средняя скорость вибрационного движения. Отклонение числа частиц 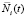 от среднего значения в любой момент времени связано с вероятностью просеивания частиц в ячейки сита, которая рассматривается как случайное событие. Эта вероятность зависит от размеров и формы самих частиц, гранулометрического состава разделяемого материала, условий стесненности и других факторов, а также от относительной скорости вибрационного движения материала. В области отверстия ячейки относительная скорость частицы может принимать любые значения от нуля до максимального. Поэтому зависимость вероятности просеивания от относительной скорости рассматривается как случайное событие с нормальным распределением [3]. В каждый фиксированный момент времени
от среднего значения в любой момент времени связано с вероятностью просеивания частиц в ячейки сита, которая рассматривается как случайное событие. Эта вероятность зависит от размеров и формы самих частиц, гранулометрического состава разделяемого материала, условий стесненности и других факторов, а также от относительной скорости вибрационного движения материала. В области отверстия ячейки относительная скорость частицы может принимать любые значения от нуля до максимального. Поэтому зависимость вероятности просеивания от относительной скорости рассматривается как случайное событие с нормальным распределением [3]. В каждый фиксированный момент времени 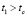 из-за различной вероятности просеивания в ячейки сит частиц выбранной фракции их число на поверхности сита
из-за различной вероятности просеивания в ячейки сит частиц выбранной фракции их число на поверхности сита 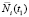 является случайной величиной, т.е. число частиц
является случайной величиной, т.е. число частиц 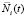 рассматривается как случайный процесс. Аппроксимация случайного процесса Ni белым шумом возможна, так как время корреляции случайного процесса много меньше среднего времени пребывания выбранных частиц на поверхности сита. С учетом свойств белого шума [8] процесс Ni является марковским процессом. Для его изучения можно использовать математический аппарат теории марковских процессов и плотность распределения
рассматривается как случайный процесс. Аппроксимация случайного процесса Ni белым шумом возможна, так как время корреляции случайного процесса много меньше среднего времени пребывания выбранных частиц на поверхности сита. С учетом свойств белого шума [8] процесс Ni является марковским процессом. Для его изучения можно использовать математический аппарат теории марковских процессов и плотность распределения 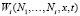 найти из решения системы уравнений Колмогорова – Фоккера – Планка (К. – Ф. – П.) [8]:
найти из решения системы уравнений Колмогорова – Фоккера – Планка (К. – Ф. – П.) [8]:
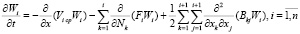 .
.
Здесь приняты обозначения: 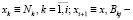 коэффициенты диффузии. Решение уравнений (К. – Ф. – П.) при больших значениях n представляет собой сложную задачу. Поэтому для изучения случайного процесса Ni построим систему стохастических дифференциальных уравнений, которые описывают его изменение вдоль сит классификатора в зависимости от времени.
коэффициенты диффузии. Решение уравнений (К. – Ф. – П.) при больших значениях n представляет собой сложную задачу. Поэтому для изучения случайного процесса Ni построим систему стохастических дифференциальных уравнений, которые описывают его изменение вдоль сит классификатора в зависимости от времени.
Рассматривается случай, когда разделяемый материал в начале верхнего сита имеет небольшую толщину (несколько слоев). Тогда кинетические функции Fi могут быть представлены в виде
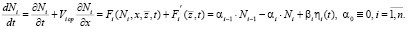 (1)
(1)
Коэффициенты кинетических уравнений вычисляются по зависимости [2]:
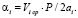 (2)
(2)
Коэффициенты αi определяют количество прохода рассматриваемых частиц через ячейку за секунду, тем самым характеризуют скорость изменения случайного процесса. Здесь приняты обозначения: P – вероятность просеивания частиц в ячейку сита, 2ai – шаг i-го сита. Вероятность просеивания в ячейку рассматривается как сложное событие, состоящее из геометрической вероятности и вероятности, которая зависит от относительной скорости вибрационного движения. Вычисление вероятности просеивания в ячейку рассмотрено в работе [3]. Вибрационное движение сыпучих сред достаточно подробно изучено в работе [1]. Вычисление средней скорости вибрационного движения и амплитуды относительной скорости, которая используется при вычислении вероятности просеивания в ячейку, приведены в работе [3]. Рассмотрим решение дифференциальных уравнений (1) при следующих начальных и граничных условиях:
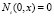 при
при 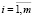 и
и 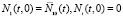 при
при 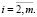 (3)
(3)
Условия (3) определяют подачу разделяемого материала только на начало верхнего яруса многоярусного классификатора, 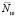 – число выбранных частиц (1/м), которые поступают на начало первого сверху сита. Используя замену
– число выбранных частиц (1/м), которые поступают на начало первого сверху сита. Используя замену 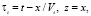 уравнения (1) с учетом условий (3) могут быть решены сведением к обыкновенным дифференциальным уравнениям [7]. Например, общее решение дифференциального уравнения для верхнего яруса можно записать в виде
уравнения (1) с учетом условий (3) могут быть решены сведением к обыкновенным дифференциальным уравнениям [7]. Например, общее решение дифференциального уравнения для верхнего яруса можно записать в виде
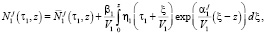
где 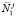 определяет среднее значение случайного процесса
определяет среднее значение случайного процесса 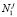 .
.
На основании решений системы (1) для каждого яруса можно определить среднее значение, корреляционную функцию и дисперсию процесса Ni. Среднее значение случайного процесса 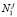 для верхнего яруса с учетом условий (3) имеет вид
для верхнего яруса с учетом условий (3) имеет вид
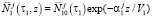 .
.
Также с учетом свойств белого шума [8] можно найти дисперсию процесса:
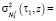
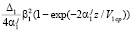 .
.
Решение дифференциального уравнения относительно среднего для второго сита из системы (1), с учетом решения для первого и условий (3), имеет вид
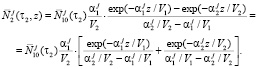
В итоге данное решение можно записать в виде
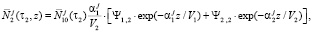
где 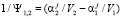 и
и 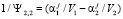 .
.
Решение дифференциального уравнения относительно среднего значения случайного процесса для третьего сита из системы (1), с учетом решений для первого и второго, а также начальных и граничных условий (3), имеет вид
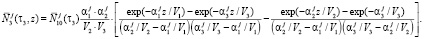
Полученное решение для третьего сита можно представить в виде
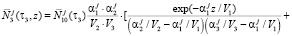
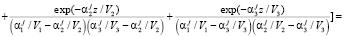
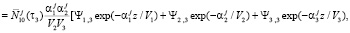
где
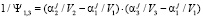 ,
,
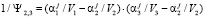 ,
,
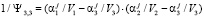 .
.
Используя метод индукции, можно показать, что решение дифференциального уравнения относительно среднего значения случайного процесса для i-го сита имеет вид
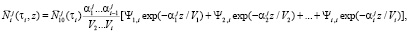 (4)
(4)
где 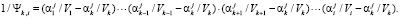
В общем случае для определения плотности распределения случайного процесса решение системы уравнений (К. – Ф. – П.) проводят численными методами. При аппроксимации белым шумом случайный процесс Ni является нормальным [8]. Поэтому, зная числовые характеристики случайного процесса, можно записать приближенное решение для плотности распределения и вероятностей перехода, которые являются фундаментальными решениями задачи Коши при дельтаобразных начальных условиях:
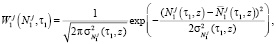
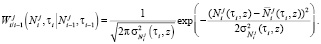
В общем случае N1 в начальном сечении является случайной величиной с плотностью вероятности 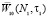 . Тогда уравнение (К. – Ф. – П.) для первого сита, с помощью замены
. Тогда уравнение (К. – Ф. – П.) для первого сита, с помощью замены
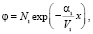
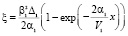 (5)
(5)
приводится к простейшему уравнению диффузии 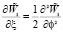 и решение полученного уравнения записывается в виде интегральной свертки:
и решение полученного уравнения записывается в виде интегральной свертки:
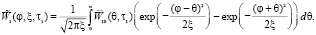 (6)
(6)
Тогда общее решение уравнения (К. – Ф. – П.) для первого сита имеет вид
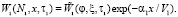 (7)
(7)
На рисунке приведены результаты расчетов изменения среднего значения случайного процесса (концентрации частиц, 1/м) целевых продуктов вдоль первого и второго сита многоярусного классификатора. На основании полученных решений вычисляются коэффициенты извлечения целевых продуктов. Также по непросеянным остаткам с сит оценивается их качество. Для этого определяется доля нецелевых продуктов (мелких), которые оказались в целевом продукте.
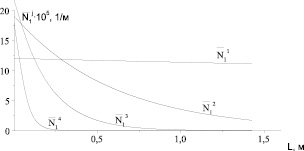
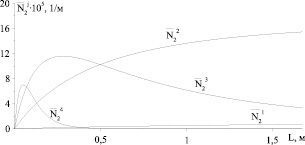
Изменение среднего значения случайного процесса (концентрации частиц, 1/м) целевых продуктов вдоль первого и второго сита многоярусного классификатора: α11 = 5,78E-3; α21 = 8,42E-2; α31 = 2,57E-1; α41 = 9,08E-1; α12 = 3,66E-4; α22 = 2,77E-3; α32 = 7,18E-1; α42 = 6,93E-1 (сек-1); Vcp = 0,05 м/сек; размеры фракций: 1 – (0,8÷0,9)·10-3; 2 – (0,7÷0,8)·10-3; 3 – (0,6÷0,7)·10-3; 4 – (0,5÷0,6)·10-3 (м)
Заключение
Теория случайных процессов с использованием результатов эксперимента для определения параметров модели позволяет строить математические модели выделения целевых продуктов из зернистых материалов на многоярусных ситовых классификаторах, которые являются основой для проведения оптимизации и управления процессом.
Библиографическая ссылка
Ахмадиев Ф.Г., Гиззятов Р.Ф., Назипов И.Т. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ КЛАССИФИКАЦИИ ЗЕРНИСТЫХ МАТЕРИАЛОВ НА СИТАХ // Современные наукоемкие технологии. 2019. № 12-1. С. 30-35;URL: https://top-technologies.ru/ru/article/view?id=37828 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/snt.37828



