При разработке нефтяных и газовых месторождений важное значение приобретает выработка наиболее рациональной системы, при которой месторождение разбуривается минимальным числом скважин, обеспечивающим при этом заданный темп добычи сырья, высокую конечную нефте – и газоотдачу [1–3]. При этом актуальным среди всего прочего становится: определение системы размещения установленного числа скважин по площади месторождения; порядок и темп ввода их в эксплуатацию; поддержание намеченного режима их работы; регулирование баланса пластовой энергии [4–6]. В связи с этим возникает необходимость математического моделирования указанных процессов с последующей оптимизацией размещения рядов скважин относительно друг друга.
В работе проведен сравнительный анализ численных решений осредненных двумерных моделей с модифицированными относительными фазовыми проницаемостями и лабораторными фазовыми проницаемостями, а также трехмерных моделей при неизотермической двухфазной фильтрации нефти в слоистых пластах.
Материалы и методы исследования
На основе вычислительного эксперимента проводится верификация известных осредненных моделей неизотермической двухфазной фильтрации в слоистых по абсолютной проницаемости нефтяных пластах относительно исходного трехмерного численного решения задачи. Получен положительный результат, подтверждающий возможности применения этих моделей при решении задачи неизотермической фильтрации.
Слоистый полосообразный нефтяной пласт разрабатывается семью рядами скважин при заданных на них давлениях. Центральный ряд закачивает в пласт горячую воду. Расположенные от него симметрично по три слева и справа добывающие ряды выкачивают нефть и воду. Двухфазная фильтрация задана в рамках математической модели Баклея – Леверетта с учетом неизотермичности потока, и от температуры зависят только вязкости воды и нефти. Рассмотрены две известные осредненные модели неизотермической двухфазной фильтрации в слоистых по абсолютной проницаемости нефтяных пластах. Где изменение абсолютной проницаемости по слоям задано с помощью конкретного вероятностного закона распределения при известных его параметрах. Рассматриваемые осредненные модели В и С подробно описаны в работах [7, 8].
В данной работе сначала решаем задачу верификации для каждой из этих двух осредненных моделей неизотермической фильтрации. Саму же задачу оптимизации на основе двумерных и трехмерных математических моделей конкретно будем решать ниже. Расчеты были проведены для случая работы трех рядов эксплуатационных скважин слева и справа от центрального ряда нагнетательных горячую воду скважин при неизотермической фильтрации при закачке в пласт горячей воды 100 град., начальная температура пласта 22 град. При расчетах использовали известный численный алгоритм и сертифицированный гидросимулятор TEMPEST [9]. ( Расчеты проводили в ТатНИПИ, нефть г. Бугульма), где реализована полностью неявная разностная схема. Рассматриваемый слоистый пласт разбивали схематично на расчетные блоки для каждой из трехмерных моделей Ai . Где имеется центральная нагнетательная воду скважина и по три слева и справа от нее эксплуатационные скважины. Для этого вырезали из пласта симметричный элемент рассматриваемого полосообразного пласта, в котором находится по одной скважине из каждого ряда, – всего семь скважин.
Результаты исследования и их обсуждение
Численные расчеты для этого симметричного элемента проводили на основе четырех указанных ниже математических моделей:
Двумерные модели (осредненные)
1. C – модель, – задачу решали при линейных, квадратичных и кубических лабораторных относительных фазовых проницаемостях (ОФП) KВ(S), KН(S) (1), средней проницаемостью k* = 0,5 дарси в двумерной постановке. Задавали один слой, высотой H = 10 м. В качестве лабораторных ОФП применяли лабораторные функции KВ(S) и KН(S) вида
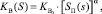
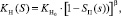
где
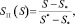
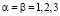. (1)
Индексы «Н» и «В» соответствуют нефти и воде, индекс «П» – подвижная водонасыщенность, «0» – максимальное значение ОФП, S* и S* – максимальная и минимальная водонасыщенность. При α = β = 1 эти ОФП – линейные, при α = β = 2, они – квадратичные.
2. В – модель, – задачу решали в двумерной постановке при модифицированных ОФП вида (2) для экспоненциального закона и вида (3) для равномерного закона при средней абсолютной проницаемости пласта k* = 0,5 дарси. Где функция абсолютной проницаемости k(z) исходного пласта задана вероятностным законом. Задавали один слой, высотой H = 10 м. Для первого закона модифицированные ОФП при линейных ОФП заданы формулой (2) работ [7, 8]. Она определяет, что модифицированные ОФП получаем из лабораторных умножением последних на определенные поправочные коэффициенты – правые скобки в формулах. Аналогично получают модифицированные ОФП и для нелинейных случаев.
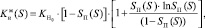
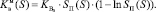(2)
На рис. 1 слева даны графики лабораторных и модифицированных ОФП для линейного случая. Аналогичные по своему взаимному расположению графики были получены для квадратичного (рис. 1, справа) и кубического случаев.
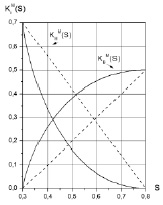
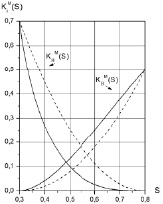
Рис. 1. Экспоненциальный закон, графики линейных ОФП (прерывистые линии) и их модифицированные аналоги (сплошные линии) (слева). Справа: графики квадратичных ОФП (прерывистые линии) и их модифицированные аналоги (сплошные линии)
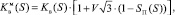
В табл. 2 даны значения абсолютной проницаемости по пропласткам для экспоненциального закона. А в табл. 3 – значения для равномерного закона. Для этого модифицированные ОФП имеют вид (1)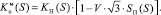, (3).
(3)
Вязкости фаз взяты в известном виде [10]
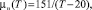
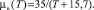(4)
Табл. 1 иллюстрирует эти функции.
Таблица 1
|
T( °C) |
μн(мПа с) |
μв(мПа с) |
μн/μв |
|
21 |
151 |
0,96 |
157,3 |
|
22 |
75,5 |
0,93 |
81,2 |
|
25 |
30,2 |
0,86 |
35,1 |
|
30 |
15,1 |
0,77 |
19,6 |
|
60 |
3,8 |
0,46 |
8,3 |
|
100 |
1,9 |
0,30 |
6,3 |
|
150 |
1,2 |
0,21 |
5,7 |
На рис. 2 приведены графики полученных модифицированных ОФП для равномерного закона распределения при максимальном значении коэффициента вариации V = 0,55. Для экспоненциального закона имеем V = 0,89.
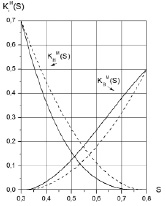
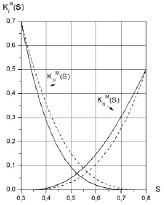
Рис. 2. Графики модифицированных ОФП для равномерного закона при квадратичных и кубических (справа) лабораторных ОФП
В моделях были заданы следующие физические параметры:
128 – начальное пластовое давление, атм;
22 – температура пласта, С;
100 – температура закачиваемой воды, С;
55 – забойное давление на третьей добывающей скважине, атм;
170 – забойное давление на нагнетательной скважине, атм;
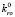= 0,5 – максимальная относительная фазовая проницаемость воды;
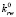= 0,7 – максимальная относительная фазовая проницаемость нефти;
Sor = 0,2 – остаточная нефтенасыщенность;
Swc = 0,3 – насыщенность связанной воды;
Sw, So – водо- и нефтенасыщенности, Swc ≤ Sw ≤ 1 – Sor , So = 1 – Sw.
Трехмерные модели (эталонные)
3. Модель A8, – численное трёхмерное решение для десятислойного пласта с изолированными слоями (отсутствуют вертикальные перетоки). Его дискретная абсолютная проницаемость подчиняется экспоненциальному закону [10,1]. Пласт образован 10 слоями, высотой H1 = H2 = H3 = H4 … H10 = 1 м. Они изолированы друг от друга непроницаемыми перемычками;
4. Модель A7, – та же, что и предыдущая, но с неизолированными слоями.
В работе были изучены 8 эталонов. Они отличаются только взаимным расположением 10 слоёв по толщине слоистого пласта, эти эталоны подчиняются экспоненциальному закону. На рис. 3, 4 даны графики только двух предельных граничных значений, – модели A7, A8.
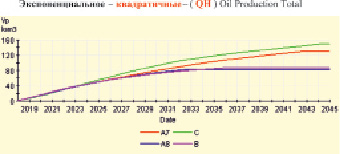
Рис. 3. Графики добычи количества нефти по годам, модели С, А7, А8, В – сверху вниз
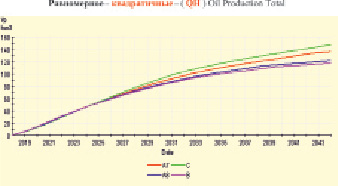
Рис. 4. Графики добычи количества нефти по годам, модели С, А7, А8, В – сверху вниз
Таблица 2
Проницаемость k(z) по слоям для модели А7 с неизолированными слоями, экспоненциальный закон, (размерность в мдарси)
|
K1 |
K2 |
K3 |
K4 |
K5 |
K6 |
K7 |
K8 |
K9 |
K10 |
|
300 |
400 |
216 |
527 |
144 |
697 |
82 |
958 |
26 |
1651 |
Таблица 3
Проницаемость k(z) по слоям для модели А7 с неизолированными слоями, равномерный закон, (размерность в мдарси)
|
K1 |
K2 |
K3 |
K4 |
K5 |
K6 |
K7 |
K8 |
K9 |
K10 |
|
450 |
550 |
350 |
650 |
250 |
750 |
150 |
850 |
50 |
950 |
Выводы по верификации осредненных моделей
На рис. 3, 4 показаны расчетные графики суммарной добытой нефти для всех четырех указанных выше моделей: при квадратичных функциях ОФП, для экспоненциального и равномерного законов. Графики моделей С и В являются верхней и нижней границами для всех эталонов. Графики эталонов находятся между графиками моделей А7 и А8.
Поэтому в каждый момент времени нам известны границы изменения для всех восьми трехмерных эталонов. И всегда можно найти их среднее значение по известному среднему значению двух осредненных моделей. Эти величины совпадают с точностью до нескольких процентов. Аналогичные положительные результаты были получены для всех основных технических показателей разработки многослойного пласта, – коэффициента нефтеотдачи, количества суммарной жидкости, воды, доли обводненности продукции в потоке на выходе, и т.д. Аналогичные положительные результаты были получены для линейных и кубических зависимостей ОП. Результаты верификации обеих моделей для этих законов получились положительными. Поэтому можно рекомендовать для расчетов неизотермической фильтрации обе осредненные модели в совокупности. Особенно их удобно применять для оценки границ, в которых находятся трехмерные эталоны. А также – при решении многовариантных задач рациональной разработки нефтяных месторождений в полосообразных многослойных пластах.
Библиографическая ссылка
Аль Джабри А.Я.А., Куан Минь Тхо, Плохотников С.П., Еникеева С.Р. РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ РАЗРАБОТКИ ПОЛОСООБРАЗНОЙ НЕФТЯНОЙ ЗАЛЕЖИ В ЗАВИСИМОСТИ ОТ РАЗМЕЩЕНИЯ РЯДОВ СКВАЖИН ПРИ НЕИЗОТЕРМИЧЕСКОЙ ФИЛЬТРАЦИИ // Современные наукоемкие технологии. – 2019. – № 12-1. – С. 20-24;URL: https://top-technologies.ru/ru/article/view?id=37826 (дата обращения: 16.04.2024).