Использование в практике школьного преподавания интегрированных уроков не дань моде. Они обеспечивают демонстрацию межпредметных связей и их применение при решении разнообразных задач, способствуют своей нестандартной формой рассмотрению не представленных в программе общеобразовательной школы вопросов из разных областей знания, повышению мотивации учебной деятельности школьников, стимулированию их мыслительных процессов, активному использованию в них анализа, синтеза, сравнения, классификации, обобщения. Однако успешная реализация возможностей, предоставляемых интегрированным уроком, напрямую зависит как от оригинальности его темы и её содержательного потенциала, так и от свободного владения со стороны учителя теми сложными вопросами, которые выносятся на такого рода занятие.
Фрактальная живопись и математическая теория фракталов – вопросы насколько интересные своей необычностью, настолько непростые для изложения в школьной аудитории и потому требующие специального рассмотрения. Ему посвящена основная часть настоящей работы, обусловливающая её актуальность.
Как известно, в последние десятилетия творческие поиски в области искусства всё чаще приводят к художественным экспериментам с применением математического инструментария. В сфере изобразительных искусств наиболее ярко эта тенденция проявилась в так называемой фрактальной живописи, авторы которой подсознательно тяготеют к использованию в изобразительных целях сходных между собой геометрических фигур.
Если художники прошлого только интуитивно обращались к этому приёму, то разработанная Бенуа Мандельбротом в средине 1970-х гг. теория фракталов – «структуры, состоящей из частей, которые в каком-то смысле подобны целому», – открыла перед живописью широкую дорогу к сознательному использованию новой техники создания визуальных образов [1].
Сочетание природосообразности, оригинальности и эстетической привлекательности фрактальной живописи обеспечила ей большую популярность в художественных кругах, что выразилось в появлении целого ряда эксплуатирующих возможности фрактального метода направлений, получивших достаточно условные, хотя и неслучайные наименования: фрактальный реализм, фрактальный абстракционизм, фрактальная монотипия и другие.
Цель исследования: прояснение характерологических черт основных разновидностей фрактального изобразительного искусства и осмысление перспектив более широкого применения теории фракталов для численной реализации его эстетических возможностей, что призвано помочь учителю, а при его посредстве и ученикам разобраться в специфике взаимодействия математической науки и искусства.
Материалы и методы исследования
Использование в процессе исследования сравнительно-исторического и типологического методов, а также методов математического анализа обеспечивает решение поставленной двуединой задачи. Вычисления проводились на программной платформе .NET Framework 4.5.1, в качестве IDE использовалась Microsoft Visual Studio 2017.
Результаты исследования и их обсуждение
Наличие в общепринятых названиях направлений фрактального искусства традиционных базовых понятий (реализм, абстракционизм, монотипия) указывает на определённую связь соответствующих направлений с художественной традицией предшествующих веков. Присутствие же рядом определения «фрактальный» обращает внимание на то, что в каждом из них изобразительно-выразительный потенциал фрактальной живописи реализуется по-своему.
Обозначенные направления находятся в стадии своего становления, и потому их типология ещё не обрела достаточную определённость, но некоторые показательные черты уже имеют место. Наиболее очевидны они у фрактального реализма [2]. Неслучайно именно это направление единственное пока обрело подготовленный Вячеславом Усейновым эстетический манифест, в котором, к сожалению, поэтика направления изложена в столь завуалированной форме, что требует специального истолкователя, на роль которого авторы статьи отнюдь не претендуют. По этой причине последующие рассуждения будут опираться исключительно на рассмотрение художественных полотен живописца и его последователей.
Реализм в изобразительном искусстве проделал долгий путь развития и представал в разных ипостасях. Очевидно, что, вынося в определение своего метода термин «реализм», Усейнов ориентировался не на классический реализм с присущим ему максимально приближенным к действительности изображением социально-психологических явлений, и не на неореализм, провозгласивший в середине XX в. возврат к реалистическим ценностям традиционных изобразительных форм.
Сам Усейнов истоки своего творчества находит в «эпохе Возрождения» и «русском авангарде 1920-х гг.». Из первого источника он очевидно почерпнул раскрепощенность духа и правдивость деталей, а из второго – свободное обращение с формой. Более близким по времени предтечей его творчества видится гиперреализм конца минувшего столетия с его искусственно-насильственным разрушением реальности обезличенной жизни современного города. Определяя особенности поэтики творчества этого художника, можно признать, что для его полотен характерно: установка на «осуществление духовного прорыва», при намеренной внешней бессобытийности, реалистичность фрагментарных микрообразов, тщательное отношение к каждому фракталу в процессе переработки определённого впечатления и преобладание мрачных тонов, создающих у зрителя соответствующее настроении.
Заметим, если Вячеслав Усейнов для обеспечения бессобытийности часто обращается к мозаично фрагментированным изображениям, то Алексей Сундуков – ещё один яркий представитель фрактального реализма – идёт прямо противоположным путём, фокусируя внимание именно на событии при большом стечении однотипных, практически безликих участников действия, лишённого целеполагания. Возникает ощущение, что автор не пишет картины, а создаёт своего рода чёрно-белые фотографии массовых действ. Это наводит на мысль о следовании художника традиции фотореализма со свойственными ему изображениями современной обыденной повседневности, в образах которой предстаёт суррогат реальности, мало одухотворенный субъективностью художника [3]. Сходства и особенно различия творческой манеры представляемых живописцев отчётливо видны при взгляде на картины «Пять солнц» В. Усейнова (рис. 1) и «Бесконечный зал» А. Сундукова (рис. 2).

Рис. 1. В. Усейнов «Пять солнц»

Рис. 2. А. Сундуков «Бесконечный зал»
Если произведения фрактального реализма в большей или меньшей степени обнаруживают связь с жизненными реалиями, то фрактальный абстракционизм отвергает её полностью по принципиальным соображениям [4]. Их суть заключается в убеждении, что подлинных высот в изобразительном искусстве можно достичь только посредством отрешения от форм самой жизни и воплощения субъективных цветовых впечатлений и фантазий художника. Именно такой подход вслед за корифеями абстракционизма Василием Кандинским, Пабло Пикассо и их многочисленными последователями реализуется в произведениях фрактального абстракционизма, пролагая путь к достижению гармонии определённых цветовых сочетаний и геометрических форм, обеспечивающих возникновение у созерцателя разнообразных ассоциаций. В этом отношении представители фрактального абстракционизма выступают непосредственными наследниками поэтики кубизма, что невооруженным взглядом видно в полотнах «Вега в красном» (рис. 3) Виктора Вазарелли и «Life Generator» Алексея Ермушова (рис. 4).

Рис. 3. В. Вазарелли «Вега в красном»
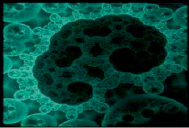
Рис. 4. А. Ермушова «Life Generator»
Значимость стихийного фактора во фрактальном абстракционизме роднит это направление изобразительного искусства со стохатипией – фрактальной монотипией, процесс создания которой сочетает в себе заданность и непредсказуемость. Это противоестественное сочетание несовместимого оказывается в данном случае возможным, более того, оно обусловлено самой технологией создания художественного полотна. В результате копирования свежего нанесённого на твёрдую поверхность рисунка путём наложения на него листа бумаги и последующего его плавного отсоединения в течение минуты после разделения соприкасавшихся поверхностей на оттиске формируется образ, который носит случайный характер и который поражает зрителей необычной расцветкой и свое-
образными узорами.
Предпринятое В.М. Лившицем в работе «Новация в области изобразительного искусства и ее научное объяснение» исследование картин «Золотой серии стохатипий» привело к формулированию доказанного в том числе опытным путём выводу, касающемуся микроструктуры изображений фрактальной монотипии. Суть этого вывода в том, что на получаемых при использовании описанной выше технологии возникают характерные для фракталов структуры, например дендритные образования. Это свидетельствует о протекании процесса самоорганизации в пленке жидкости между твёрдой поверхностью и бумагой новых структурных образований, вследствие чего на бумаге возникает оттиск с необычными узорами, которые не могут быть повторены художником даже целенаправленно. Подтверждение тому – картина Лео Лившиц «Зима» (рис. 5) и «Колыбельная» Влада Лившица (рис. 6).
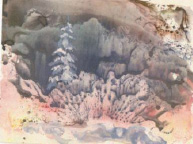
Рис. 5. Лео Лившиц «Зима»

Рис. 6. Влад Лившиц «Колыбельная»
На их полномасштабных изображениях отчётливо видны и размытость очертаний воссоздаваемых объектов, и фрактальность микроструктуры, благодаря которым возникает ощущение какой-то особой лёгкости и прозрачности рисунка, что, однако, не предопределяет характер его эмоционального фона, который может быть самым разным.
Характеризуя особенности стохатипии, следует признать её сопряжение не только с фрактальным абстракционизмом, но и с фрактальным реализмом, так как, создавая посредством оригинальной техники своеобычные изображения, авторы этого направления отталкиваются от жизненных реалий, которые легко угадываются в их художественных полотнах. Эта установка на использование реалистической основы обусловливает тематическое многообразие творений фрактальной монотипии. В итоге стохатипия, благодаря таким сопряжениям обретает наибольшую свободу в выборе отображаемых объектов и эмоционального самовыражения художника.
Предложенный сжатый обзор основных направлений фрактальной живописи позволяет констатировать не только явные различия их первоистоков и техники создания художественных изображений, но и очевидную общность микроструктур, обеспечивающих многоуровневое подобие составляющих художественные полотна компонентов, общность, достигаемую как посредством использования традиционных приёмов написания картин, так и применением специальных компьютерных программ, в основу которых положена теория фракталов. Знание и понимание основ этой теории способно открыть перед художником дополнительные возможности для более полной реализации эстетического потенциала фрактальной живописи, а перед учителем – путь к результативному проведению интегрированного урока математики и изобразительного искусства.
Фракталами являются объекты геометрической природы, обладающие подобием. Окружающие художника подобные друг другу природные объекты могут быть с высокой степенью точности описаны посредством фракталов и запечатлены с помощью IT технологий и компьютерной графики. В итоге такая работа сводится к изучению составных фрагментов представленного изображения и количественных параметров.
Основной характеристикой цифрового фрактального изображения служит размерность, она определяет вид и сложность фрактала. Для определения размерности объекта применяют топологическую и фрактальную размерность. Наибольший интерес имеет фрактальная размерность, для ее вычисления разобьем n-мерное пространство на кубы с ребром a. Пусть N(a) – количество кубиков, необходимое для полного покрытия фрактального множества, тогда фрактальная размерность определяется по формуле
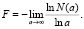
Также характеристикой цифрового фрактального изображения является коэффициент формы
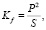
где P – периметр изображения, S – площадь. Параметр определяет уровень излома границы изображения.
Следующим параметром выступает энтропия цифрового фрактального изображения. Термин энтропия понимается как мера количества информации, необходимая для характеристики системы в заданном измерении. Энтропию также трактуют как единицу отклонения от равновесного состояния. Для вычисления энтропии используем формулу
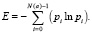
Для неравновесных функций энтропия принимает положительное значение, а для равновесных, гладких – отрицательное.
Вычисление описанных характеристик реализовано численно [5] на программной платформе .NET Framework 4.5.1.
Заключение
Проведённое исследование специфики основных направлений фрактальной живописи – фрактального реализма, фрактального абстракционизма и фрактальной монотипии (стохатипии) – показало, что наличие фрактальной основы в произведениях рассмотренных направлений изобразительного искусства, обеспечивая их определённое родство, в то же время не препятствует использованию принципиально различных подходов к организации их художественного мира и не исключает существенных расхождений в интенсивности использования элементов фрактальной структуры создаваемых художественных полотен. Прослеживается прямая зависимость между характером применённой техники исполнения рисунка, в частности её «ручного» или компьютерного варианта, и достигаемым художником эффектом. Показательно, что наибольшего успеха пока удаётся достичь стохатипии при условии тщательного подхода к подбору используемого материала и процедуре отделения оттиска от исходного рисунка.
Надеемся, что представленная нами в концентрированном виде теория фракталов в её приложении к проблемам фрактальной живописи поможет учителю донести до сознания школьников реальность сопряжения науки и искусства, сформировать у них представления о специфике фракталов, пробудить способность сопоставлять на первый взгляд несопоставимое, развить умение анализировать сравнивать и классифицировать поступающую в различной форме информацию, побудить к её самостоятельному поиску и дальнейшей обработки.
Библиографическая ссылка
Торшина О.А., Торшина В.В. К ВОПРОСУ О ПОДГОТОВКЕ ИНТЕГРИРОВАННОГО УРОКА МАТЕМАТИКИ И ИЗОБРАЗИТЕЛЬНОГО ИСКУССТВА // Современные наукоемкие технологии. 2019. № 11-2. С. 374-378;URL: https://top-technologies.ru/ru/article/view?id=37821 (дата обращения: 05.03.2026).



