С каждым днём растёт актуальность применения беспилотных летательных аппаратов (БПЛА) для решения межотраслевых задач. С помощью беспилотных технологий осуществляется фото-видеосъёмка окружающего пространства, дистанционный анализ окружающих объектов, доставка грузов, контроль состояния транспортных магистралей, добывающих комплексов. Также БПЛА используют на аварийно опасных участках, где присутствие людей сопряжено с опасностью для жизни.
При управлении беспилотным летательным аппаратом возникают проблемы взаимодействия со статическими объектами, в особенности когда он находится в автономном режиме управления. Требуются математические алгоритмы, позволяющие эффективно осуществлять распознание рельефа местности, с целью определения препятствий и выбора траектории их облёта.
Целью работы является разработка алгоритмов и их автоматизация, позволяющих на основе потоков информации, поступающих с сенсоров летательного аппарата вычислять глубину пространства (расстояния до объектов) и при наличии препятствий определять траекторию их облёта. Из-за технологических особенностей летательных аппаратов накладываются ограничения по использованию дополнительного оборудования на борту, поэтому требуется разработка алгоритмов использующих минимум сенсоров.
Материалы и методы исследования
Существуют следующие типы датчиков (сенсоров) для получения информации беспилотным летательным аппаратом об окружающем пространстве: – радары, лазерные (лидары), ультразвуковые (сонары) и оптические системы видимого спектра (стерео- и монокамеры). Область применения каждого типа сенсоров ограничена по-разному. Радары имеют низкую точность определения формы и расстояния до объектов на траектории полёта. Лидары обладают плохой точностью при погодных явлениях, ограничивающих видимость, кроме того высокая стоимость (более 100 тыс. руб.) делает решения на их основе недоступными для массового сегмента БПЛА. Сонары способны обнаруживать препятствия лишь на небольших расстояниях. Использование монокамер (одной камеры) не позволяет определить глубину пространства без применения других сенсоров либо иных внешних факторов. Стереокамера же сочетает в себе относительно невысокую стоимость, небольшой вес, возможность с высокой точностью осуществлять распознание рельефа местности, что позволяет её устанавливать на массовом сегменте беспилотных летательных аппаратов [1].
В данной работе не преследуется цель создания конечного коммерческого решения по организации систем дистанционного зондирования, а рассматривается модель реализации систем стереозрения, формирующих информационный поток для автоматического построения траектории полета в реальном времени. Для решения поставленной задачи [2] создаётся экспериментальный прототип стереокамеры и строится система определения глубины пространства, с достаточной степенью точности оценки (расстояния до объектов) на основе потоков графической информации».
В качестве образца выбраны камеры с минимальными техническими характеристиками: тип матрицы – CMOS; число мегапикселей матриц – 1,3 МП; разрешение – 1280х720; максимальная частота кадров – 30 кадр/c; фокусировка – фиксированный фокус от 40 см; расстояние между камерами – 14 см.

Рис. 1. Горизонтальная «стереокамера»
На рис. 2 рассматривается система, состоящая из двух камер. C – центр левой камеры; C' – центр правой камеры, X – точка пространства; x – проекция X на плоскость изображения (рассматриваются растровые изображения размером MxN пикселей) левой камеры; x' – проекция X на плоскость изображения правой камеры; луч xX – прообраз точки x на изображении левой камеры; l' – эпиполярная линия, являющаяся проекцией xX на плоскость правой камеры.
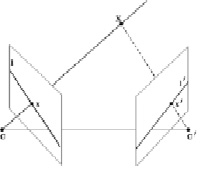
Рис. 2. Проекция точки пространства на изображения с камер
Каждой точке x на изображении левой камеры соответствует эпиполярная линия l' на изображении правой камеры. При этом пара для x на изображении правой камеры может лежать только на соответствующей эпиполярной линии. Аналогично, каждой точке x’ на правом изображении соответствует эпиполярная линия l на левом.
Для получения корректных данных проводится единожды процесс калибровки камер, определяется пространственное соответствие между двумя изображениями, обеспечивающее возможность сдвига только по оси х. Этапы процесса калибровки приведены на рис. 3.

Рис. 3. Этапы калибровки стереокамеры
Для каждой точки левого изображения с координатами (x0, y0) выполняется поиск точки на правом изображении. Точка на правом изображении имеет координаты (x0 – d, y0), где d – величина, называемая смещением (рис. 4). Сформированная карта глубин представляет собой двумерный массив размером MxN, где каждый элемент ai,j содержит информацию о расстоянии от плоскости камеры до наблюдаемой точки в пространстве.
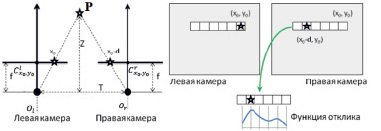
Рис. 4. Вычисление карты глубин
Программная реализация осуществляется на базе ОС Ubuntu 16.04 LTS под управлением ROS (Robot Operating System) Kinetik. ROS является популярной платформой, ориентированной на использование в мобильных роботах, в том числе и в БПЛА, что позволяет внедрить разрабатываемое ПО почти в любую существующую систему под его управлением. ROS обеспечивает стандартные службы операционной системы, такие как аппаратную абстракцию, низкоуровневый контроль устройств, реализацию часто используемых функций, передачу сообщений между процессами и управление пакетами. ROS основан на архитектуре графов, где обработка данных происходит в узлах, которые могут получать и передавать сообщения между собой. В ROS поддерживается программирование на языках C++ и Python.
Создание экспериментальной модели для определения глубины пространства состоит из следующих этапов:
1. Для получения потоков графической информации, поступающих на обработку, создаётся программный модуль usb-cam. Данный модуль запускает два узла usb_cam_node – для получения видеопотока синхронизированных во времени с обеих камер в разрешении MxN – 640x480 с частотой кадрой в 30 FPS (Frames Per Second).
2. Проводится калибровка камер [3]. Используется калибровочный образец формата А3 – шахматный узор, закреплённый к жёсткой, ровной поверхности [4].
3. Программным путём производится ректификация изображений [5], выполняется поиск соответствующих пар точек, формируется карта глубин размером получаемого видеопотока – 640х480. Определяются оптимальные параметры для качественной визуализации карты глубин. На рис. 5, а, представлен видеопоток с левой камеры, на рис. 5, б видеопоток с правой камеры, на рис. 5, в получаемая карта глубины (рис. 5).
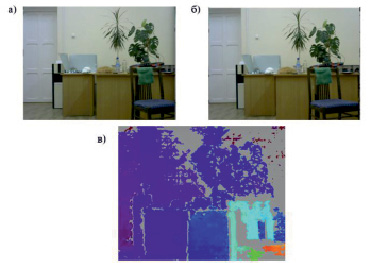
Рис. 5. Видеопоток с обеих камер и сформированная карта глубины: а) видеопоток с левой камеры, б) видеопоток с правой камеры, в) сформированная карта глубины
Каждый пиксель карты глубины рассматривается в виде десятичного RGB кода, состоящий из вектора с тремя компонентами цвета – красный, зелёный, синий, принимающий значения в диапазоне от 0 до 255. Экспериментальным путём получаемый RGB код соотносится со значением расстояния в метрической системе от плоскости камер до объекта и сохраняется в массиве расстояний. Полученные результаты приводятся в табл. 1.
Таблица 1
RGB код и соответствующее ему значение в метрической системе
|
№ |
Расстояние, м |
Код RGB (r,g,b) |
Градиент |
|
1 |
1,44–1,64 |
(255,0,0) – (255, 235,0) |
|
|
2 |
1,64–1,92 |
(255, 235,0) – (15,255,0) |
|
|
3 |
1,92–2,32 |
(15, 255,0) – (0,255, 245) |
|
|
4 |
2,32–2,92 |
(0,255, 245) – (2,2,255) |
|
|
5 |
2,92–3,84 |
(2,2,255) – (53,0,255) |
|
|
6 |
3,84–4,64 |
(53,0,255) – (83, 0, 125) |
|
Согласно табл. 1 видно, что градиент сине-фиолетового цвета обозначает дальнее расстояние объектов от плоскости камеры, а красного – близкое расстояние.
С целью определения точности построения карты глубины производится съёмка в помещении, определяется расстояние до различных объектов (рис. 6). Полученные результаты сравниваются с данными лазерного дальномера CONDTROL Smart 40 c погрешностью ± 1,5 мм. Данные измерений приводятся в табл. 2.

Рис. 6. Определение расстояний до разных окрестностей точек по карте глубины: а) окрестность А, Б, В; б) окрестность Г, Д; в) окрестность Е, Ж, З; г) окрестность И, К, Л
Таблица 2
Расстояние до разных областей помещения
|
Измеряемая область |
Данные карты глубин, м |
Данные дальномера, м |
Расхождение, м |
Относительная |
|
Область А |
4,64 |
4,68 |
–0,04 |
0,86 |
|
Область Б |
2,36 |
2,42 |
–0,06 |
2,5 |
|
Область В |
2,82 |
2,91 |
–0,09 |
3,1 |
|
Область Г |
2,99 |
3 |
–0,01 |
0,33 |
|
Область Д |
1,58 |
1,6 |
–0,02 |
1,26 |
|
Область Е |
2,76 |
2,73 |
0,03 |
1 |
|
Область Ж |
3,08 |
3,06 |
0,02 |
0,65 |
|
Область З |
2,17 |
2,16 |
0,01 |
0,46 |
|
Область И |
2,31 |
2,24 |
0,07 |
3,03 |
|
Область К |
1,63 |
1,64 |
–0,01 |
0,61 |
|
Область Л |
3,84 |
3,88 |
0,04 |
1,04 |
а)
б)
в)
г)
Согласно табл. 2, относительная погрешность всех измерений не превышает 3,1 %, что показывает достоверность получаемых результатов для стереокамеры обычных usb-web камер.
С целью оптимизации карты глубин предварительно обрабатываются. В соответствии с табл. 1 на карте глубин выделяются критические области – объединение № 1–3. Окраска областей формируется в зависимости от их дальности.
Получаемая карта глубин содержит серый цвет – это «помехи», зоны в которых из-за однотонности области сцены невозможно подобрать парную точку на втором изображении получаемой с камеры, для расчёта смещения. С целью устранения этих зон разрабатывается алгоритм сглаживания, который закрашивает построчно данные области, анализируя соседние пиксели. Блок-схема алгоритма приводится на рис. 7.
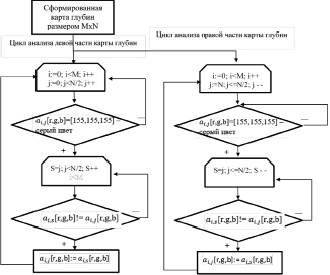
Рис. 7. Блок-схема алгоритма сглаживания карты глубин



а) изображение с камеры б) необработанная карта глубин в) обработанная карта глубин
Рис. 8. Обработанная и необработанная карты глубин
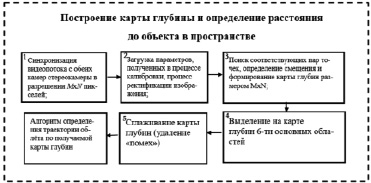
Рис. 9. Общая схема этапов работы программно-аппаратного комплекса
Пример обработанной карты глубин представлен на рис. 8.
На рис. 9 приводится общая схема, описывающая процесс построения карты глубины и определение расстояния до объекта в пространстве.
Алгоритма выбора траектории облёта препятствий на основе анализа карты глубин.
Во время полёта беспилотного аппарата видеопоток с определённой частотой кадров в момент времени k поступает в програм-
мный блок для обработки и построения карты глубин. Алгоритм выбора траектории облёта препятствий заключается в разбиении получаемой карты глубин на области – центральной (является ведущей), верхней, правой, левой.
Производится точечный анализ ведущей области, в случае обнаружения критических зон (расстояние менее 2,3 м) производится цикл анализа соседних областей с целью определения возможной траектории отклонения. Для минимизации времени анализа всех областей применяется параллельное программирование. На основе полученных данных определяется область отклонения, выбирается вектор направления движения и посылается набор команд на блок управления двигателями квадрокоптера для смены мощности винтов в соответствии с той областью, куда необходимо отклониться. На рис. 10 представлена блок-схема разработанного алгоритма.
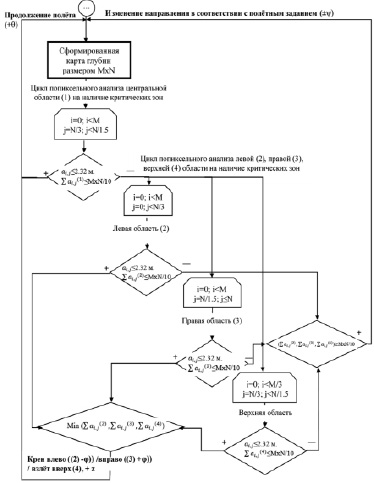
Рис. 10. Блок-схема алгоритма определения траектории облёта препятствий
на основе анализа карты глубин беспилотным аппаратом
Результаты исследования и их обсуждение
В работе рассматриваются модели компьютерного зрения и их апробация при решении задач пилотирования БПЛА [6]. Приводится вариант реализации системы стереозрения для оценки полученных результатов в лабораторных условиях и реализуется модель выбора траектории движения беспилотного летательного аппарата. С целью реализации системы автопилотирования с возможностью облёта статических препятствий на основе видеопотока с высокоэффективного оборудования производится численное моделирование в виртуальной среде Gazebo (рис. 11).
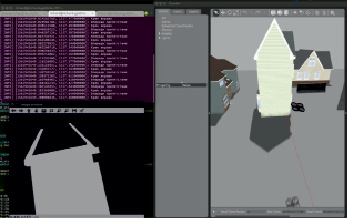
Рис. 11. Моделирование облёта статических препятствий в Gazebo
Заключение
Разработана модель программно-аппаратного комплекса автопилотирования БПЛА с возможностью обхода препятствий со сложной компоновкой объектов в 3D пространстве. Реализован экспериментальный образец системы стереозрения, проведен экспериментальный анализ по построению карт глубин помещения. Полученные результаты позволяют достаточно точно оценить расположение объектов и определить траектории беспрепятственного перемещения в пространстве.
Библиографическая ссылка
Шишов Р.И., Григорьев Я.Ю., Григорьева А.Л., Жарикова Е.П. РАЗРАБОТКА МОДЕЛИ ОПРЕДЕЛЕНИЯ ГЛУБИНЫ ПРОСТРАНСТВА ДЛЯ ЗАДАЧ ДЕТЕКТИРОВАНИЯ ПРЕПЯТСТВИЙ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА // Современные наукоемкие технологии. 2019. № 11-2. С. 306-313;URL: https://top-technologies.ru/ru/article/view?id=37809 (дата обращения: 05.03.2026).









