Известно, что для получения качественной продукции при металлообработке, в частности на токарном станке, следует автоматически поддерживать статическое значение сил резания, что позволяет обеспечить точность геометрических размеров детали, а также повышения стойкости инструмента, поскольку нагрузки на их меняется в небольших пределах [1, 2].
В связи с этим определенный интерес представляет теоретическое исследование объекта управления, имеющего безынерционный и инерционный регуляторы расхода, поступающего в рабочую полость цилиндра гидросуппорта.
Цель исследования: разработка математических моделей разрабатываемых систем, анализ их динамических характеристик, влияние регуляторов на вид и длительность переходных процессов и возможность применения результатов математических исследований для практики.
Методы исследования основаны на основных положениях теории автоматического управления, механики и гидроавтоматики.
Результаты исследования и их обсуждение
Дифференциальное уравнение объекта регулирования гидросуппорта станка имеет вид
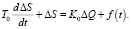 (1)
(1)
Дифференциальное уравнение инерционного регулятора представляется в виде [3, 4]:
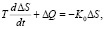 (2)
(2)
где Т – постоянная времени регулятора, характеризующая инерционность регулятора.
Решая совместно уравнения (1) (2), найдем уравнения динамики всей системы регулирования.
Из уравнения (1) определяем
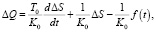
тогда
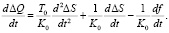 (3)
(3)
Подставляя значения и в уравнение (1), получим
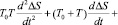
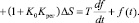 (4)
(4)
Процесс регулирования складывается из переходного и установившегося процессов [3–5]:
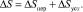 (5)
(5)
Составим характеристическое уравнение автоматической системы:
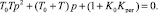 (6)
(6)
Корни характеристического уравнения представлены в виде
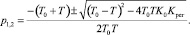 (7)
(7)
Корни характеристического уравнения будут вещественными и отрицательными при условии:
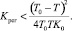 (8)
(8)
Тогда переходный процесс будет происходить по апериодическому закону второго порядка, и он складывается из двух экспонентов с разными постоянными времени:
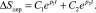 (9)
(9)
Либо
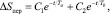 (10)
(10)
где
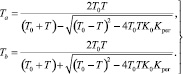 (11)
(11)
При этом из (11) видно, что Ta > Tb.
Следует отметить, что С1 и С2 произвольные постоянные, которые определяются из начальных условий.
Например,
?Sпер = C при t = 0;
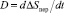 при t = 0. (12)
при t = 0. (12)
Различные варианты апериодических переходных процессов представлены на рис. 1.
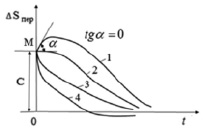
Рис. 1. Различные варианты апериодических переходных процессов
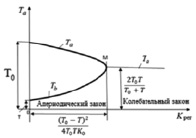
Рис. 2. Влияние Крег на характер переходного процесса
Предположим точка М (рис. 1) соответствует заданному значению ?Sпер = C при t = 0, а производная 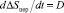 при t = 0, что соответствует кинематической скорости протекания процесса, а геометрически – наклону касательной положительной при, t = 0, то переходный процесс опишется кривой – 1, если она равна нулю – кривой 2, если она отрицательна, то кривыми 3 и 4. Математически эти кривые переходных процессов описываются формулой (10).
при t = 0, что соответствует кинематической скорости протекания процесса, а геометрически – наклону касательной положительной при, t = 0, то переходный процесс опишется кривой – 1, если она равна нулю – кривой 2, если она отрицательна, то кривыми 3 и 4. Математически эти кривые переходных процессов описываются формулой (10).
Коэффициенты С1 и С2 определяются следующим образом:
Продифференцируем уравнение (10) по времени:
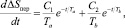 (13)
(13)
Подставляя в формулы (10) и (13) значения С и D согласно (12) при t = 0, получим
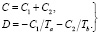 (14)
(14)
Решая эти уравнения, совместно определяем значения С1 и С2.
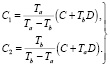 (15)
(15)
Таким образом по формуле (10) с учетом значений постоянных в (15) строятся кривые апериодического процесса (рис. 1).
При этом граничный случай этого процесса будет, когда параметры системы удовлетворяют вместо условия (8) условию
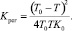 (16)
(16)
При этом получается, что корни характеристического уравнения равны
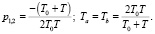 (17)
(17)
И уравнение переходного процесса будет
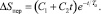 (18)
(18)
Продифференцируем по времени (12):
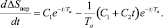 (19)
(19)
Подставляя в уравнения (12) и (13) начальные условия (8), получим два уравнения:
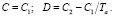 (20)
(20)
Постоянные интегрирования равны
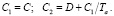 (21)
(21)
Исследуем влияние параметров регулятора на качество переходного процесса в системе автоматического управления.
При заданных значениях T0 и T будем менять коэффициент усиления регулятора Крег в пределах:
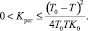 (22)
(22)
Видим, что при значениях близких к нулю, Ta ≈ T0 и Tb ≈ T, далее при увеличении Крег Ta уменьшается, а Tb возрастает, что можно наглядно показать на рис. 2.
Из (13) видно, что переходный процесс состоит из двух экспонент, постоянные времени которых Ta и Tb изменяются в пределах:
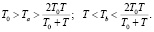 (23)
(23)
Из графиков наглядно видно, что вторая экспонента затухает быстрее, поскольку то есть в конце переходного процесса превалирует первая экспонента и по ней в принципе можно определить длительность переходного процесса, не производя решения дифференциального уравнения (13):
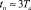 .
.
Следует отметить, что при C > 0 и D > 0 вторая экспонента вычитается из первой, что позволяет утверждать, что длительность переходного процесса будет несколько меньше, чем 3Та, но не вблизи точки М (рис. 2).
В связи с тем, что коэффициенты С1 и С2 согласно (15) увеличиваются, а в точке М длительность переходного процесса уже будет несколько выше, чем 3Тa.
При Та < Т0 присоединение регулятора к объекту уменьшает время переходного процесса за счет уменьшения инерционности объекта, а увеличение Крег в пределах (19) является весьма полезным.
С другой стороны, увеличение постоянного времени регулятора Т (рис. 2) неблагоприятно сказывается на быстроте затухания переходного процесса в системе, поскольку Та и Тb становятся больше.
Рассмотрим случай увеличения коэффициента усиления регулятора:
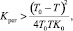 (24)
(24)
тогда корни характеристического уравнения (7) будут комплексными сопряженными:
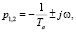 (25)
(25)
где
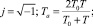
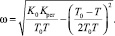
При этих корнях переходный процесс будет колебательным:
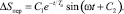 (26)
(26)
Постоянные интегрирования С1 и С2 определяются из тех же начальных условий (10):
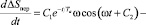
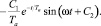 (27)
(27)
При t = 0 получаем
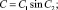
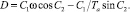 (28)
(28)
Решая совместно эти два уравнения, получаем
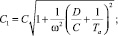
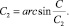 (29)
(29)
Переходный процесс будет колебательным по синусоиде, амплитуда которой затухает по экспоненте с постоянным по времени Ta. Переходный процесс представлен на рис. 3.
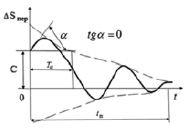
Рис. 3. Переходный процесс 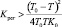
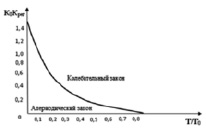
Рис. 4. График зависимости К0Крег от Т/Т0 , определяющий два вида переходного процесса
Длительность переходного процесса можно вычислить tn ≈ 3Ta. Величина Ta, согласно (25) не зависит от значения коэффициента усиления регулятора, это видно из графика (рис. 2) и формулы (16).
Следует отметить, что в автоматическом регуляторе постоянной времени Т не приносит эффекта при увеличении коэффициента усиления Крег сверх значений, представленного в выражении (16) с точки зрения быстроты затухания переходного процесса системы, но полезным с точки зрения уменьшения статической ее ошибки.
С другой стороны, возрастание постоянной времени регулятора Т замедляет затухание переходного процесса в системе автоматического управления – увеличение значения Тa.
Частота колебания регулируемой величины в переходном процессе, что видно из (19), повышается с увеличением Крег, а увеличение последнего, как это видно из (24), приводит к повышению колебательности системы регулирования, так как система успевает за время переходного процесса совершить необходимое количество колебаний.
Особый интерес представляет зависимость Крег на границе, апериодичности (16) от постоянного времени регулятора Т и параметров объекта (T0, K0), для этого построим график по формуле (16) К0Крег от величины T/T0 (рис. 4).
Из графика (рис. 4) при данном значении T/T0, если еще взять значение К0Крег выше кривой, то согласно (24), переходный процесс будет колебательным, ниже – апериодическим.
Графики, а также формулы (18) и (11) позволяют определить величины Ta, Tb, ω.
Следует заметить, что чем больше постоянная времени Т, тем скорее можно оказаться в колебательной зоне.
Кривая на рис. 4 помогает наглядному представлению о влиянии параметров регулятора на вид переходного процесса и осуществлению правильного выбора параметров системы.
Исследование установившегося процесса, например, при мгновенном скачко-
образном изменении нагрузки f(t) по закону, f(t) = const = f0.
В этом случае систематические свойства системы регулирования не зависят от Т-постоянной времени регулятора.
С другой стороны, для уменьшения статической ошибки системы регулирования, следует увеличивать Крег, но в то же время существует противоречие с требованием по качеству переходного процесса, по которому следует выбирать значения Крег вблизи величины (16).
Рациональное значение Крег следует находить с учетом статического и динамического расчетов системы регулирования.
Процесс регулирования системы складывается из переходного и установившегося режимов:
?S = ?Sпер + ?Sуст.
Если корни характеристического уравнения системы вещественны, как было отмечено выше, то имеем следующее решение [5, 6]:
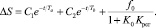 (30)
(30)
Постоянные противоречия С1 и С2 определяются из условия, что до появления скачкообразной нагрузке система работала в установившемся режиме.
Имея в виду уравнения (1) (2) объекта и регулятора в этих условиях, получим
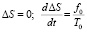 при t = 0. (31)
при t = 0. (31)
Продифференцируем по времени:
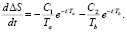 (32)
(32)
Используя (31) и (32) из уравнения (30),
получим
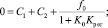
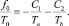 (33)
(33)
Решая совместно эти два уравнения, определяем, что
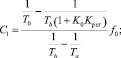
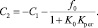 (34)
(34)
Процесс регулирования для этого случая будет выражаться следующим уравнением:
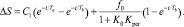 (35)
(35)
Такая методика определения процесса регулирования применима при условии, когда 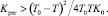
На рис. 5 построены графики переходного процесса объекта без регулятора с безынерционным регулятором и объекта инерционным регулятором при разных соотношениях Крег.
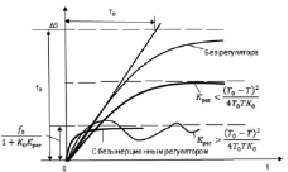
Рис. 5. Переходные процессы объекта без регулятора и с регуляторами безынерционным и инерционным
Анализ графиков, представленных на рис. 5, показывает, что в системе объект + инерционный регулятор с постоянного времени Т, можно добиться малой статической ошибки регулирования как в случае с безынерционным регулятором, но при этом переходный процесс будет колебательным.
Условия устойчивой работы объекта с инерционным регулятором:
1. Положительность коэффициентов дифференциального уравнения системы (15), то есть 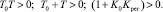
2. При отрицательных знаках вещественных корней характеристического уравнения р1,2 < 0.
3. Если корни характеристического уравнения являются комплексными сопряженными, то вещественная ее часть должны быть отрицательной.
Выводы
1. Разработана математическая модель, описывающая динамические процессы объекта регулирования – гидросуппорта с инерционным регулятором (4), позволяющая теоретически произвести расчет массо-геометрические и режимные параметры системы.
2. Установлено, что в случае присоединения к гидросуппорту инерционный регулятор, переходный процесс может по двум экспонентам, что соответствует уравнению (19), а при Kрег > (T0 – T)2/4T0TK0 переходный процесс будет колебатель-
ным (рис. 3).
3. Разработанные математические модели, расчет и анализ, проведенные в статье, позволяют правильно и рационально спроектировать автоматическую систему регулирования подачи инструмента гидросуппорта токарного станка.
Библиографическая ссылка
Кадыров И.Ш., Темирбеков Ж.Т., Турусбеков Б.С., Давлятов У.Р. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГИДРОСУППОРТА СТАНКА С ИНЕРЦИОННЫМ РЕГУЛЯТОРОМ // Современные наукоемкие технологии. 2019. № 11-2. С. 280-285;URL: https://top-technologies.ru/ru/article/view?id=37804 (дата обращения: 05.03.2026).



