Как показывают исследования [1], дисперсное армирование, например, пластиковыми [2], стальными [3, 4], биологическими [5] волокнами улучшает механические характеристики материалов. Такое упрочнение основывается на предположении, что матрица композита перераспределяет напряжения по поверхности волокон. При модуле упругости волокна большем, чем матрицы, считается что основную часть приложенных напряжений воспринимают волокна, а общая прочность композиционного материала пропорциональна их объемному содержанию.
Существующие теории об определении упругих характеристик фиброкомпозитов основываются на различных гипотезах [6]. В большинстве случаев авторы используют эмпирические зависимости [7]. Экспериментальные данные, касающиеся модуля упругости фиброкомпозитов, также весьма противоречивы.
Введение коротких дискретных волокон в материал матрицы композита можно использовать для противодействия и предотвращения распространения трещин. Одной из основных проблем, препятствующих более широкому внедрению фиброкомпозитов, является отсутствие эффективных методов расчета конструкций из фиброкомпозитов на трещинообразование. Фиброкомпозит, в отличие от некомпозита, сохраняет прочность после образования трещин.
Численное исследование имеет первостепенное значение для описания локализации деформации и инициирования трещины, т.е. для определения условий возникновения сильных напряжений и, следовательно, появления трещин [8].
Цель исследования: построение упрощенной математической и соответствующей численной модели дисперсно-армированного композита.
Материалы и методы исследования
Используется вариационный метод построения системы уравнений метода конечных элементов. Будем рассматривать шестигранный конечный элемент [9] с включенными в него фибрами.
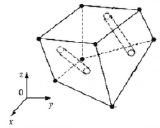
Шестигранный конечный элемент с двумя фибрами
В основе модели лежит предположение о слабом влиянии изгибных характеристик армирующего наполнителя – фибры на свойство материала, а существенным считается только влияние сжатия и растяжения фибры. Это позволило описать фибры стержневыми конечными элементами. Так что перемещения концов фибры выражаются через перемещения узлов конечного элемента, в котором находится фибра. Это позволило, не увеличивая размерность итоговой алгебраической системы уравнений, описывать упругое поведение композита, заполненного фибрами. Потенциальная энергия деформации в данном случае будет состоять из потенциальной энергии связующего всего элемента без фибр за вычетом потенциальной энергии связующего в области пространства, занимаемого фибрами и потенциальной энергии фибр.
Результаты исследования и их обсуждение
Для вывода уравнений понадобятся известные формулы теории упругости и метода конечных элементов [9]. Представим их здесь в матричном виде.
В матричной форме связь между деформацией ε и перемещением U и деформацией может быть записана в виде
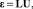(1)
где
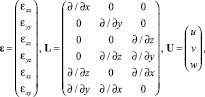
u, v, w – перемещение вдоль осей x, y, z соответственно.
Закон Гука в матричной форме: 
, где матрица c определяет упругие свойства материала,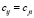 
, 
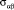– компоненты тензора напряжений.
Рассмотрим элемент с nd узлами, имеющими координаты xi (в трехмерном случае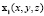 
), где i – номер узла 
.
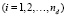Представим функции (например, перемещение по оси x) следующим образом:
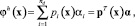(2)
где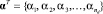 
. Для трехмерного шестигранного 8-узлового элемента:
.
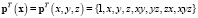Заметим, что количество компонент этого вектора равно количеству узлов элемента.
Коэффициенты αi определяются из условия равенства искомой функции (перемещений по оси x) в узлах (2)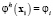 
, т.е. из решения системы линейных алгебраических уравнений:
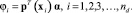(3)
В матричной форме можем записать так
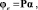(4)
где 
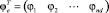и
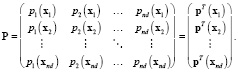
Из (4) можно получить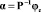 
. Подставляя это выражение в (2), получим
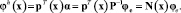(5)
Где матрица N называется функцией формы:
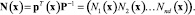
Состояние равновесия или движения деформируемых систем наряду с дифференциальными уравнениями может описываться с помощью вариационных принципов. Например, с помощью принципа наименьшего действия Гамильтона: из всех допустимых перемещений наиболее вероятным является перемещение, соответствующее минимуму функционала Лагранжа. Математически принцип Гамильтона выражается формулой: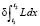 
Функционал Лагранжа
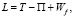(6)
где T – кинетическая энергия, П – потенциальная энергия (энергия деформированного тела), Wf – работа внешних сил.
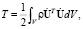(7)
где V – объем твердого тела, U – множество допустимых перемещений.
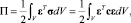(8)
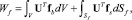(9)
где Sf – поверхность тела, на которую действуют внешние силы, fb – плотность объемных сил, fs – плотность поверхностных сил.
После разбиения тела на конечные элементы необходимо деформации (перемещения) интерполировать некоторой функцией, используя значения перемещений в узлах элемента. Например, для перемещения по направлению оси x:
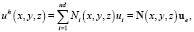
где h означает приближенное слагаемое, nd – число узлов элемента,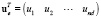 
. Для трехмерной задачи:
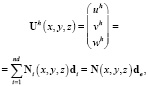(10)
где uh, vh, wh – приближенные значения перемещений вдоль осей x, y, z соответственно.
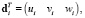(11)
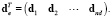(12)
Матрица функций формы N будет иметь вид
,
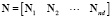где
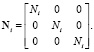
Так как согласно (1)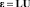 
, а согласно (10) 
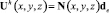, то выражение (8) будет выглядеть
Обозначив
(13)
(матрица напряжений), получим
Обозначим интеграл
(14)
и назовем его матрицей жесткости (для восьмиузлового элемента это матрица размера 24x24). Тогда
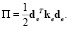(15)
Аналогично рассмотрев выражение для кинетической энергии (7), получим
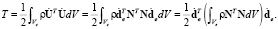(16)
Введем обозначение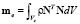 
и назовем эту матричную величину матрицей масс. Тогда (16) запишется в виде
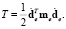(17)
Работа внешних сил (9) с учетом (10) запишется
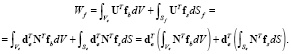
Введя обозначения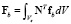 
и 
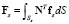, получим
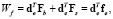(18)
где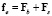 
– вектор действующих на элемент сил. Подставляя (16–18) в Лагранжиан (6), получим
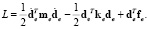(19)
Применяя принцип Гамильтона, получим: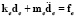 
.
Потенциальная энергия в рассматриваемой задаче с фибрами будет состоять из: потенциальной энергии связующего всего элемента без фибр ПН за вычетом потенциальной энергии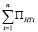 
связующего в области пространства, занимаемого фибрами и потенциальной энергии фибр ПTi.
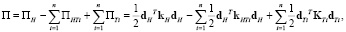
где n – количество фибр, входящих в данный конечный элемент. Индекс T (truss) обозначает стержневой элемент, H (hexagon) – шестигранный элемент. Согласно определению матрицы жесткости (14):
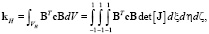
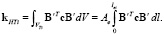
Согласно (13): 
. Элементы входящей в данное выражение матрицы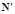 
будут определены ниже (21).
В глобальной системе координат матрица жесткости запишется в виде: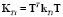 
, где T – матрица перехода от локальной системы координат, связанной с конечным элементом, к глобальной. Лагранжиан (19) будет выглядеть как
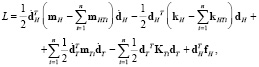(20)
где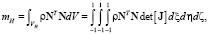 
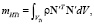
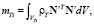ρ – плотность связующего, ρT – плотность фибры.
Согласно (3):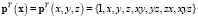 
, 
.
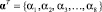Тогда получим систему линейных алгебраических уравнений для нахождения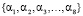 
: 
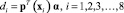, где di – узловые перемещения (например, по оси x).
Тогда, с учетом (5):
,
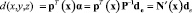где
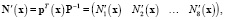(21)
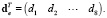
Из (11), (12) получим: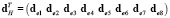 
, dej – вектор перемещения j-го узла: 
,
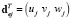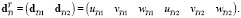
Тогда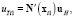 
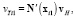
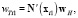
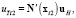
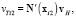
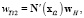где x1, x2 – радиусы векторы концевых точек i-й фибры. uH, vH, wH – векторы перемещений узлов шестигранника, соответствующие осям координат, например,
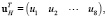
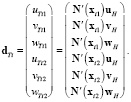
Введем матрицу
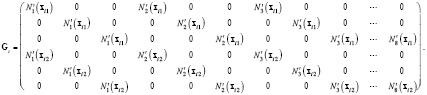
Тогда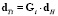 
. Лагранжиан (20) будет выглядеть как
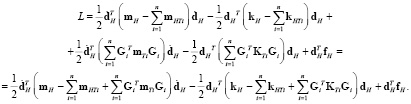
Применяя принцип Гамильтона, окончательно получим систему алгебраических уравнений для нахождения перемещений узлов шестигранного конечного элемента с фибрами, представленными стержневыми конечными элементами:
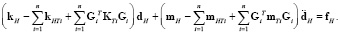
Заключение
На основе данной конечноэлементной модели составлена компьютерная программа, позволяющая рассчитывать прочность и жесткость конструкций из фиброкомпозита. Была проведена проверка модели на основе сравнения с результатами расчетов, полученными прямым методом в программе ANSYS Static Structural. Расчеты проводились только для конструкций с малым количеством фибр из-за большой вычислительной трудоемкости прямого метода. При данной проверке результаты обоих методов совпали.
Библиографическая ссылка
Галиев И.М., Самакалев С.С. КОНЕЧНОЭЛЕМЕНТНАЯ МОДЕЛЬ ДИСПЕРСНО-АРМИРОВАННОГО КОМПОЗИТА // Современные наукоемкие технологии. – 2019. – № 11-2. – С. 258-263;URL: https://top-technologies.ru/ru/article/view?id=37801 (дата обращения: 21.11.2024).