В настоящее время научные приложения, ориентированные на проведение крупномасштабных научных экспериментов в гетерогенной распределенной вычислительной среде (ГРВС), играют существенную роль в процессе решения важных практических задач на основе математического моделирования исследуемых систем [1]. Как правило, такие приложения реализуются в виде распределенных пакетов прикладных программ (РППП). Гетерогенность среды подразумевает использование в ней узлов (персональных компьютеров, серверов, кластеров, облачных платформ) с разными программно-аппаратными архитектурами и вычислительными характеристиками.
Схемы решения задач в РППП представляют собой спецификацию процесса вычислений в ГРВС. Они строятся на вычислительных моделях ГРВС, представляющих собой частный случай семантической сети. Для построения схем решения задач используются методы планирования вычислений и информационного планирования.
Для эффективного решения задач в ГРВС и рационального использования ее ресурсов необходима возможность оценки времени выполнения схем решения этих задач. В статье предложены новые модели прогнозирования времени выполнения таких схем в ГРВС. Эти модели позволяют, в отличие от известных моделей аналогичного назначения [2–4], учитывать различные оценки времени выполнения модулей, входящих в состав схем. В их числе оценки, получаемые на основе методики динамического анализа времени выполнения программ, предложенной авторами статьи [5] и используемой в процессе непрерывной интеграции прикладного программного обеспечения разрабатываемых пакетов [6].
Модели прогнозирования времени выполнения схем решения задач
Вычислительная модель ГРВС определяется структурой
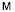 = <ASP, Z, F, M, PR, S, J,
= <ASP, Z, F, M, PR, S, J,
R, A, Q, PLCS, MH, O>,
где ASP, Z, F, M, S, J, R, A, Q, O – это соответственно множества пакетов прикладных программ, параметров, операций, программных модулей, продукций, схем решения задач, заданий, ресурсов, агентов, ограничений на выполнение заданий и использование ресурсов, накладываемых множеством PLCS административных политик, а также отношений между перечисленными объектами. Структура данных MH отражает вычислительную историю работы модулей из M. Детальное описание компонентов модели можно найти в [5, 7].
Операции из F определяют отношения вычислимости на множестве параметров Z. Параметры могут быть представлены скалярами, векторами, матрицами различных базовых типов данных или произвольными структурами данных. Каждая операция fi∈F реализуется модулем mj∈M, где 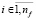 ,
, 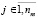 , nf – число операций, nm – число модулей. Один модуль может реализовать несколько операций. С каждой операцией fi связано два подмножества параметров
, nf – число операций, nm – число модулей. Один модуль может реализовать несколько операций. С каждой операцией fi связано два подмножества параметров 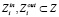 .
. 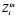 включает параметры, значения которых необходимо задать, чтобы получить значения параметров из
включает параметры, значения которых необходимо задать, чтобы получить значения параметров из 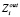 . Параметры подмножеств
. Параметры подмножеств 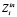 и
и 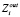 отражают назначение и семантику формальных параметров модуля mj, реализующего операцию fi. Параметры передаются между модулями в виде файлов.
отражают назначение и семантику формальных параметров модуля mj, реализующего операцию fi. Параметры передаются между модулями в виде файлов.
Процессы решения задач в пакетах представлены схемами из S. Схема s∈S выполнения операций из F является аналогом строгой параллельной формы графа алгоритма, а ее построение сходно с построением данной формы [8]. В рамках рассматриваемой вычислительной модели схема является связным подграфом ориентированного ациклического двудольного графа, представляющего схемные знания об алгоритмах исследования предметной области. На рис. 1 представлен пример такого графа. Операции и параметры изображены на нем закрашенными и незакрашенными кружками.
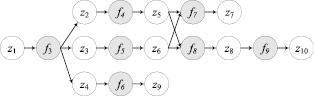
Рис. 1. Двудольный ориентированный граф схемы решения задачи
С целью поддержки общности планирования вычислений при построении схем решения задач с использованием их постановок в вычислительной модели выделяются две специальные операции f1 и f2 [9], моделирующие в дальнейшем условия задачи, подмножество параметров, значения которых заданы, и подмножество параметров, значения которых нужно вычислить. Операция f1 определяет подмножества 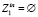 и
и 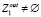 , а операция f2 обуславливает подмножества
, а операция f2 обуславливает подмножества 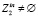 и
и 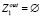 . В приведенном выше примере
. В приведенном выше примере 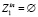 и
и 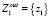 , а
, а 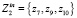 и
и 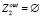 .
.
Прогнозирование времени выполнения схем решения задач здесь и ниже базируется на подходе к оценке производительности вычислительных устройств, предложенном в [7]. Пусть матрица P размерности k×k представляет сведения о предшествовании k операций схемы решения задачи. Элемент pij = 1 (pij = 0) матрицы P означает, что выполнение операции fi в схеме решения задачи предшествует (не предшествует) выполнению операции fi и 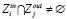 . Матрица
. Матрица 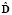 размерности k×k отражает оценки объемов передаваемых данных между операциями. Элемент матрицы
размерности k×k отражает оценки объемов передаваемых данных между операциями. Элемент матрицы 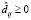 показывает объем данных, передаваемых операцией fi операции fj. Матрица W размерности k×k предоставляет информацию о пропускной способности интерконнекта между узлами, в которых запускаются модули, реализующие операции схемы. Элемент матрицы wij ≥ 0 демонстрирует пропускную способность интерконнекта между узлами, в которых работают модули, реализующие операции fi и fj. Тогда оценка
показывает объем данных, передаваемых операцией fi операции fj. Матрица W размерности k×k предоставляет информацию о пропускной способности интерконнекта между узлами, в которых запускаются модули, реализующие операции схемы. Элемент матрицы wij ≥ 0 демонстрирует пропускную способность интерконнекта между узлами, в которых работают модули, реализующие операции fi и fj. Тогда оценка 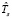 времени выполнения схемы в асинхронном режиме по готовности данных определяется следующим образом:
времени выполнения схемы в асинхронном режиме по готовности данных определяется следующим образом:
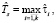 ,
,
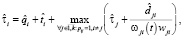
где 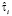 (
(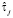 ) – оценка времени, прошедшего с начала обработки схемы до завершения операции fi (fj),
) – оценка времени, прошедшего с начала обработки схемы до завершения операции fi (fj), 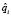 – оценка времени нахождения в очереди модуля, реализующего операцию fi (в то время, когда все данные, необходимые для его выполнения, готовы),
– оценка времени нахождения в очереди модуля, реализующего операцию fi (в то время, когда все данные, необходимые для его выполнения, готовы), 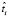 – прогнозная оценка времени выполнения этого модуля, k – число операций схемы, 0 < ωji(t) ≤ 1 – коэффициент снижения пропускной способности интерконнекта в момент времени t между узлами, в которых функционируют модули, реализующие операции fi и fj.
– прогнозная оценка времени выполнения этого модуля, k – число операций схемы, 0 < ωji(t) ≤ 1 – коэффициент снижения пропускной способности интерконнекта в момент времени t между узлами, в которых функционируют модули, реализующие операции fi и fj.
Пусть матрица S размерности m×k представляет собой ярусно-параллельную форму, описывающую обработку схемы в режиме fork/join, m – число ярусов схемы. Элемент sli = 1 означает, что операция fi должна быть выполнена на l-м ярусе. Переход к операциям (l + 1)-го яруса возможен при условии завершения всех операций на l-м ярусе. Тогда оценка 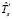 времени выполнения схемы в режиме fork/join находится следующим образом:
времени выполнения схемы в режиме fork/join находится следующим образом:
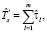
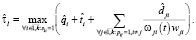
Оценка 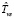 времени выполнения схемы в среде с виртуализированными ресурсами в асинхронном режиме определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами в асинхронном режиме определяется следующим образом:
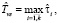
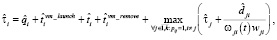
где 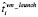 и
и 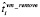 – это соответственно оценки времени на запуск и завершение ВМ для выполнения модуля, реализующего операцию fi. Оценки
– это соответственно оценки времени на запуск и завершение ВМ для выполнения модуля, реализующего операцию fi. Оценки 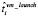 и
и 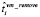 определяются экспериментальным путем для ВМ различной конфигурации.
определяются экспериментальным путем для ВМ различной конфигурации.
Оценка 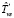 времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
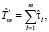
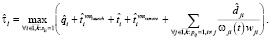
Оценка 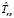 времени выполнения схемы в асинхронном режиме с рестартом модулей определяется следующим образом:
времени выполнения схемы в асинхронном режиме с рестартом модулей определяется следующим образом:
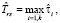
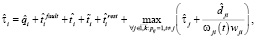
где 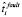 и
и 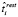 – это соответственно оценки времени обнаружения и идентификации отказа, а также повторного запуска (рестарта) модуля, реализующего операцию fi, в случае программно-аппаратного отказа. Оценки
– это соответственно оценки времени обнаружения и идентификации отказа, а также повторного запуска (рестарта) модуля, реализующего операцию fi, в случае программно-аппаратного отказа. Оценки 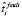 и
и 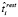 определяются средним временем выполнения таких процессов системой метамониторинга для разных видов программно-аппаратных отказов,
определяются средним временем выполнения таких процессов системой метамониторинга для разных видов программно-аппаратных отказов, 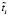 – время выполнения модуля до отказа.
– время выполнения модуля до отказа.
Оценка 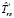 времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
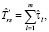
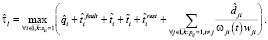
Оценка 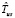 времени выполнения схемы в асинхронном режиме по готовности данных на основе пользовательских оценок времени выполнения модулей определяется следующим образом:
времени выполнения схемы в асинхронном режиме по готовности данных на основе пользовательских оценок времени выполнения модулей определяется следующим образом:
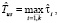
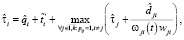
где 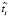 – пользовательская оценка времени выполнения модуля.
– пользовательская оценка времени выполнения модуля.
Оценка 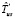 времени выполнения схемы в режиме fork/join определяется следующим образом:
времени выполнения схемы в режиме fork/join определяется следующим образом:
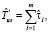
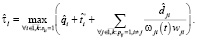
Оценка 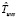 времени выполнения схемы в среде с виртуализированными ресурсами в асинхронном режиме определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами в асинхронном режиме определяется следующим образом:
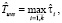

Оценка 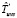 времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
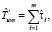
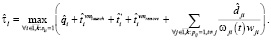
Оценка 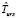 времени выполнения схемы в асинхронном режиме с рестартом модулей определяется следующим образом:
времени выполнения схемы в асинхронном режиме с рестартом модулей определяется следующим образом:
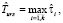
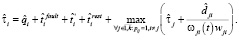
Оценка 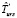 времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
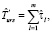
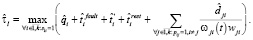
Оценка 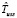 времени выполнения схемы в асинхронном режиме по готовности данных на основе пользовательских оценок времени выполнения модулей определяется следующим образом:
времени выполнения схемы в асинхронном режиме по готовности данных на основе пользовательских оценок времени выполнения модулей определяется следующим образом:
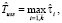
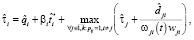
где 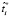 – скорректированная пользовательская оценка времени выполнения модуля, βi = ψ(i, MH, Th) > 0 – это корректирующий коэффициент, вычисляемый на основе вычислительной истории. Функция ψ(i, MH, Th) вычисляет значение коэффициента βi, используя среднее или медианное значения по выборке времени выполнения модуля, реализующего операцию fi, за определенный период Th.
– скорректированная пользовательская оценка времени выполнения модуля, βi = ψ(i, MH, Th) > 0 – это корректирующий коэффициент, вычисляемый на основе вычислительной истории. Функция ψ(i, MH, Th) вычисляет значение коэффициента βi, используя среднее или медианное значения по выборке времени выполнения модуля, реализующего операцию fi, за определенный период Th.
Оценка 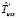 времени выполнения схемы в режиме fork/join определяется следующим образом:
времени выполнения схемы в режиме fork/join определяется следующим образом:
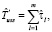
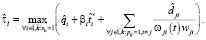
Оценка 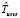 времени выполнения схемы в среде с виртуализированными ресурсами в асинхронном режиме определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами в асинхронном режиме определяется следующим образом:
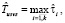
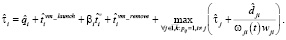
Оценка 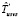 времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
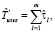
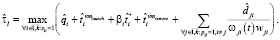
Оценка 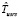 времени выполнения схемы в асинхронном режиме с рестартом модулей определяется следующим образом:
времени выполнения схемы в асинхронном режиме с рестартом модулей определяется следующим образом:
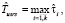
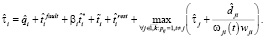
Оценка 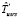 времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
времени выполнения схемы в среде с виртуализированными ресурсами соответственно в режиме fork/join определяется следующим образом:
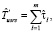
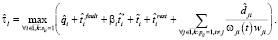
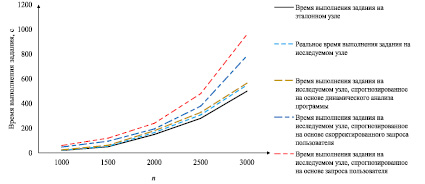
Рис. 2. Результаты реального и прогнозируемого времени выполнения заданий по перемножению матриц
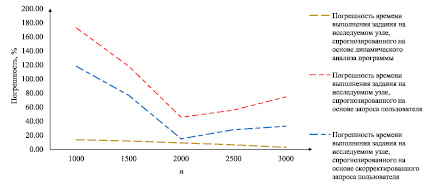
Рис. 3. Погрешность прогнозируемого времени выполнения заданий
В качестве примера проведем сравнение погрешности различных способов прогнозирования времени выполнения заданий для задач линейной алгебры (перемножение матриц размерности n×n). Задачи решались в ГРВС, организованной на базе ресурсов Центра коллективного пользования «Иркутский суперкомпьютерный центр СО РАН» [10], в процессе непрерывной интеграции (модификации, контроля версий, сборки, тестирования, доставки и размещения) модулей, реализующих операции линейной алгебры. На рис. 2 приведены результаты времени выполнения заданий по перемножению матриц для n = 1000, 1500, 2000, 2500, 3000 одной и той же программой на эталонном и исследуемом узлах, а также время выполнения этих заданий, определенное с помощью трех способов его прогнозирования, рассмотренных выше.
Очевидно, что наиболее точный прогноз формируется на основе динамического анализа программ. На рис. 3 приведены погрешности различных способов прогнозирования времени выполнения заданий в сравнении с реальным временем их выполнения в исследуемом узле. Результаты, приведенные на рис. 3, показывают, что погрешность времени выполнения задания, спрогнозированного на основе динамического анализа программы, убывает с увеличением размерности матриц. В данном примере она не превышает 13,64 %. В то же время изменение погрешности времени выполнения задания, спрогнозированного на основе запроса пользователя, может иметь немонотонный характер. На практике время выполнения задания, спрогнозированного на основе запроса пользователя, как правило, завышается. Корректировка времени в запросе пользователя на основе вычислительной истории его заданий может уменьшить погрешность прогнозирования.
Заключение
Рассмотренные в статье модели прогнозирования схем решения задач в ГРВС будут использованы в процессе децентрализованного управления вычислениями [6].
Работа выполнена при поддержке РФФИ, проект № 19-07-00097-А и Президиума РАН, программа № 7, проект «Методы, алгоритмы и инструментальные средства децентрализованного группового решения задач в вычислительных и управляющих системах».
Библиографическая ссылка
Феоктистов А.Г., Башарина О.Ю. МОДЕЛИ ПРОГНОЗИРОВАНИЯ ВРЕМЕНИ ВЫПОЛНЕНИЯ СХЕМ РЕШЕНИЯ ЗАДАЧ В ГЕТЕРОГЕННОЙ РАСПРЕДЕЛЕННОЙ ВЫЧИСЛИТЕЛЬНОЙ СРЕДЕ // Современные наукоемкие технологии. 2019. № 11-1. С. 102-108;URL: https://top-technologies.ru/ru/article/view?id=37773 (дата обращения: 05.03.2026).
DOI: https://doi.org/10.17513/snt.37773



