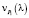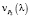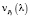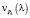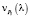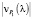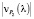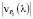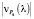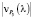В современных реалиях становится все более актуально разрабатывать научные подходы в областях энергосбережения и ресурсосбережения [1, 2]. Для их создания необходимо прибегнуть к решению оптимизационных задач различной степени трудности [3, 4]. Для реализации современной и научной идеи или для формирования верного управленческого решения на различных уровнях, необходимо предпринять меры к снижению временных затрат на проведение поискового исследования [5, 6].
Для реализации данной цели требуется разрешить проблемы из областей информатики [7, 8] и кибернетики [9, 10], которые являются взаимосвязанными. Рассматриваемые во времени системы управления процессов обработки информации требуют улучшения. При прохождении различных этапов поискового исследования возможно решение кибернетических проблем на каждом из этапов. Каждый этап обладает своими проблемами обработки информации, решение которых даст новое знание, где протекание процессов во времени не является главенствующим. В связи с этим авторы статьи проводят изучение и оптимизацию процесса поискового исследования, с использованием информационно-вычислительных технологий. Данный материал является продолжением их кропотливой работы над когнитивным процессом выбора наилучшей альтернативы из множества существующих вариаций [11–13].
В ходе проведенных исследований по получению оптимальной системы выбора авторы статьи использовали современные подходы к структурированию информации, например прибегли к методу ментальных карт [14, 15]. Прежде поисковое исследование как система не исследовалась. В большинстве случаев улучшались и оптимизировались сами этапы поискового исследования.
Авторы статьи ранее установили [11, 12], что поисковое исследование – это когнитивный процесс S, который состоит из пяти этапов: 1 – литературно-патентный обзор; 2 – изучение математических моделей; 3 – изучение методов решения; 4 – сравнение методов решения; 5 – выбор метода решения. Этапы являются случайными вероятностными процессами. В случайный момент времени любой этап может быть хорошо выполнен и будет происходить переход на другой этап. В противном случае мгновенно начинается когнитивное исправление нужного этапа. Состояния когнитивных этапов Pi, где i = 1, …, 5, соответствуют когнитивным процессам системы. Переходы между когнитивными этапами происходят мгновенно в случайные моменты времени после завершения текущего этапа. Для их анализа и определения значения вероятности нахождения в каждом из этих этапов авторы предложили использовать граф состояний [12], где окружности – это состояния системы. Переходы между состояниями обозначаются стрелками. Из описания системы и формулировки задачи видно, что к ней применим метод составления и решения уравнений Колмогорова. Следует заметить, что авторы впервые сформулировали данную задачу и предложили решить её данным методом. Ранее данный метод применялся к решению других актуальных вероятностных задач [16–18].
Материалы и методы исследования
Для каждого этапа поискового исследования существуют свои разные по эффективности методологии создания управляющего информационного обеспечения и свои информационные системы, которые обрабатывают информацию. Их эффективность необходимо рассматривать в количественных показателях, зависящих от времени t. Качественные показатели эффективности зависят от анатомии и технологии добывания знания [9]. Поисковое исследование имеет дело с потоком научной информации, которая соответствующим образом обрабатывается на каждом этапе. Поэтому качественным показателем эффективности i-го этапа поискового исследования, где i = 1, …, 5, можно считать интенсивность информационного потока научной информации [19]. Он равен объёму полезных знаний для решения следующего этапа, полученный за время выполнения текущего. Интенсивность потока в некотором смысле является математическим ожиданием M(x) количества событий в единицу времени [20] и отражает интенсивность работы ученого. Научные исследования характеризуются нестандартными потоками, которые характерны для неустановившегося процесса. Их интенсивность меняется в течение определенного периода времени:
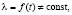 (1)
(1)
где f(t) – это кривая на трёхмерной плоскости Pi, в системе координат xyz (рис. 1), где ось x – это интенсивность потока; y – это вероятность состояния системы Pi, где i = 1, …, 5; z – это время t. При учёте проекции плоскости Pi на систему координат xy, необходимо рассматривать лишь зависимости Pi(λ) – финальные вероятности (рис. 2), которые были получены авторами через решение системы уравнений Колмогорова [11]. Финальные вероятности равны
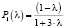 – график вероятности первого этапа, (2)
– график вероятности первого этапа, (2)
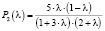 – график вероятности второго этапа, (3)
– график вероятности второго этапа, (3)
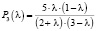 – график вероятности третьего этапа, (4)
– график вероятности третьего этапа, (4)
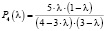 – график вероятности четвёртого этапа, (5)
– график вероятности четвёртого этапа, (5)
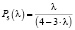 – график вероятности пятого этапа. (6)
– график вероятности пятого этапа. (6)
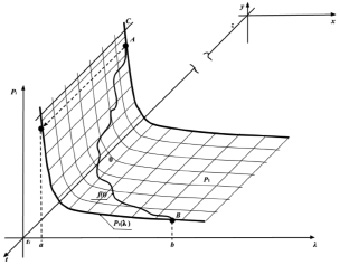
Рис. 1. Перемещение точки по плоскости P1 в пространстве xyz рядом с финальной вероятностью P1(λ)
Плотность потока можно выразить следующим образом [14]:
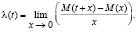 (7)
(7)
Для простейшего потока уравнение (7) можно записать так:
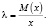 (8)
(8)
Имеет место дискретное равномерное распределение, поэтому
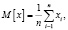 (9)
(9)
где xi – значение из интервала [a; b].
Пусть результатом выполнения i-го события является некоторое количество знаний Δзi. Тогда результатом выполнения j-го события будет определение области Δhi, в которой отсутствуют знания, необходимые для решения задачи (рис. 3). Используя уравнение (9), проведём аналогию для простейшего потока событий в поисковом исследовании, где значением из интервала [a; b] будет количество знаний Δзi или количество незнания Δhi, выявленное событием:
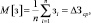 (10)
(10)
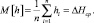 (11)
(11)
Если приравнять единице максимальное количество полезных знаний, которые можно получить за интервал времени Δt, то можно записать ΔHcp = 1–Зср. Для соблюдения размерностей при расчёте и изображении зависимостей в системе координат xyz, H и З будем рассматривать в долях. Подставим уравнения (10) и (11) в (8) и получим интенсивности потока событий, учитывая равенство x = Δt:
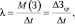 (12)
(12)
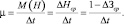 (13)
(13)
Для системы xyz интенсивность ещё можно получить следующим образом:
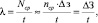 (14)
(14)
где Nср – это среднее число событий в единицу времени t;
nср – это среднее количество элементарных событий Δз;
Δз – это положительный исход i-го события, результатом которого стала информация, представляющая интерес для решения текущей задачи;
ΔЗ – это некое количество знаний, полученное в единицу времени t.
Финальные вероятности, как функции от ΔЗ, получены подстановкой уравнения (12) или (14) в уравнения (2)–(6):
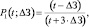 (15)
(15)
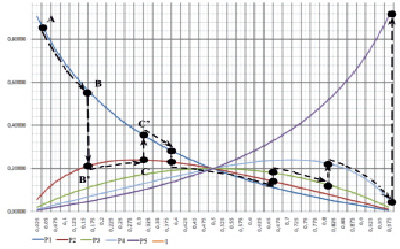
Рис. 2. Перемещение точки по графикам зависимости P1(λ), P2(λ), P3(λ), P4(λ) и P5(λ) на плоскости xy
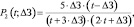 (16)
(16)
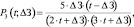 (17)
(17)
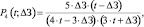 (18)
(18)
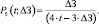 (19)
(19)
Рассмотрим рис. 1. На нём изображена плоскость P1, которая соответствует вероятности пребывания процесса поискового исследования на первом этапе. Первым этапом процесса является литературно-патентный обзор, который был выбран случайным образом для визуализации примера и объяснения теории данной статьи. Аналогично можно брать для рассмотрения и другие плоскости: P2, P3, P4 и P5, которые могут быть получены аналогичным образом из проекций на плоскость xy финальных вероятностей: P2(l), P3(l), P4(l) и P5(l). Такой подход возможен, если рассматривать плоскость вблизи финальных вероятностей. Рассматриваемый период времени близок к моменту завершения поискового исследования и несоизмеримо мал со всем временем, которое было затрачено на поисковое исследование. Для проведения более точных исследований и анализа всех этапов поискового исследования необходимо использовать плоскости, которые могут быть получены из уравнений (15)–(19) путём пошаговой подстановки значений t и З. Таким образом будут получены более точные изображения плоскостей P1, P2, P3, P4 и P5. Необходимо заметить, что З будет соответствовать , так как они отображаются в одинаковой размерности и связаны формулой (12).
Для плоскости P1 финальная вероятность имеет вид функции P1(λ). Если с течением времени не происходит событий с положительным исходом, то ход процесса поискового исследования можно изобразить прямой линией C, которая расположена на плоскости P1. Или запишем C∉P1. После появления событий с положительным исходом кривая движения процесса поискового исследования будет определена зависимостью f(t) ≠ const, которая также будет расположена на плоскости P1 или f(t)∈P1. Функцию P1(λ) можно считать проекцией функции f(t) на плоскость xy. Чтобы не нарушить единство существующих законов математики, физики и обработки информации, будем учитывать скорость движения точки в пространстве на плоскостях xyz и xy, не учитывая массу точки и разные виды энергии. Процесс поискового исследования можно представить перемещающейся точкой на плоскости P1 или на графике P1(λ). Характеристикой хода данного процесса может стать скорость движения v нематериальной точки. Если рассматривать движение точки в системе координат xyz, то нужно рассматривать путь от точки A до точки B по кривой f(t), которая f(t)∈P1. Если для расчёта v учитывать перемещение точки по проекции f(t) на плоскость xy, то нужно рассматривать путь от точки Ay до точки B по кривой P1(l), которая P1(λ)∈P1. Необходимо скорость движения такой точки рассматривать как вектор, который раскладывается на составляющие в декартовых координатах. Так как закон сохранения энергии не принимается в расчёт, то при переходе точки с одной плоскости Pi на другую плоскость Pj, скорость будет рассчитываться заново, исходя из новых сложившихся условий. Такой переход будет мгновенным. Намерение начать следующий этап поискового исследования запускает новый когнитивный процесс с найденным количеством знаний З, полученным за временя t.
Приведём пример. Пусть в точке B происходит переход на следующий этап поискового исследования – изучение математических моделей. Тогда, учитывая уравнение (12), можно записать
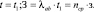 (20)
(20)
Если полученного З недостаточно для выполнения текущего этапа, то произойдёт моментальный переход на нужный этап поискового исследования. Он происходит сразу же после того, как проблема будет зафиксирована и будет принято решение запустить новый этап.
Точка может перемещаться по плоскостям P1, P2, P3, P4 и P5 и с плоскости на плоскость в последовательности, которая может зависеть от сложившихся внешних условий. Предлагаемая авторами модель может учесть различные случаи: от идеального до самого худшего, который может занять наибольшее время t. Графическое изображение процесса движения точки по плоскостям можно представить в виде кривой fxz(t) на плоскости xz – вид сверху (рис. 3). Перемещение точки можно представить её перемещением по графикам зависимости P2(l), P3(l), P4(l) и P5(l) в плоскости xy (рис. 2).
Рассмотрим перемещение по отрезку [D; E] кривой fxz(t) на плоскости xz (рис. 4). Данный отрезок кривой расположен на плоскости Pi. Можно записать следующее для перемещения точки по плоскости Pi:
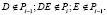 (21)
(21)
Рисунок помогает получить картину общего движения точки с момента начала работ до их завершения, как плоскую проекцию движения точки на плоскость xz. К сожалению, рисунок не даёт увидеть переходы с одной плоскости на другую. В момент перехода с плоскости Pi-1 на плоскость Pi точка D сначала принадлежит плоскости Pi-1(D∈Pi-1), а потом принадлежит плоскости Pi(D∈Pi-1). На рис. 5 переход не виден, так как на виде сверху на плоскость xz он изображается одной точкой (точкой D). Записанные уравнения (21) становятся понятны при визуализации перемещения точки по финальным вероятностям P1(l), P2(l), P3(l), P4(l) и P5(l) на плоскости xy (рис. 2).
Решение
Получим выражение для скорости движения точки по графикам зависимости P1(l), P2(l), P3(l), P4(l) и P5(l) на плоскости xy. Запишем проекции скорости на оси декартовой системы координат:
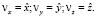 (22)
(22)
Вектор скорости в декартовых координатах:
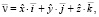 (23)
(23)
где 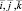 – это единичные орты.
– это единичные орты.
Тогда модуль вектора скорости равен
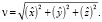 (24)
(24)
Для рассмотрения конкретных случаев и определения ускорения точки необходимо учитывать проекции скорости на оси y и z, так как ось z отражает ось времени. При ускоренном движении скорость равна
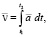 (25)
(25)
где 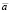 – это ускорение точки;
– это ускорение точки;
t1 ≤ t ≤ t2 – это отрезок времени, в течение которого рассматривается скорость.
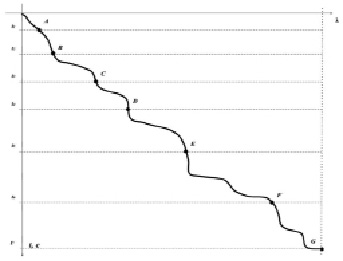
Рис. 3. Графическое изображение процесса движения точки по плоскостям в виде кривой fxz(t) на плоскости xz – вид сверху
Далее подробно рассмотрим движение точки по плоскости xy, которая отражает график зависимости финальной вероятности Pi от своей проекции движения. Скорость точки равна:
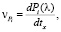 (26)
(26)
где
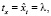 (27)
(27)
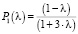 (28)
(28)
уравнение, которое было получено авторами в предыдущем исследовании [20] для графика вероятности первого этапа.
Подставим уравнения (27) и (28) в (26) и получим выражение для скорости движения точки по графику P1(l):
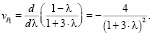 (29)
(29)
Минус в итоговом выражении говорит о том, что точка движется против оси y, то есть оси P1. Действительно, она спускается вниз по графику финальной вероятности P1(l) или по представленной на рис. 1 плоскости P1.
Аналогичным образом можно вывести формулы для скоростей перемещения точки по оставшимся графикам вероятностей:
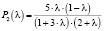 – график вероятности второго этапа, (30)
– график вероятности второго этапа, (30)
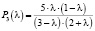 – график вероятности третьего этапа, (31)
– график вероятности третьего этапа, (31)
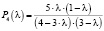 – график вероятности четвёртого этапа, (32)
– график вероятности четвёртого этапа, (32)
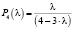 – график вероятности пятого этапа. (33)
– график вероятности пятого этапа. (33)
Будем подставлять в уравнение (26) последовательно уравнение (27) и уравнения (30)–(33). Результаты запишем ниже:
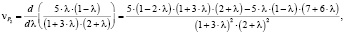 (34)
(34)
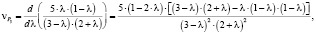 (35)
(35)
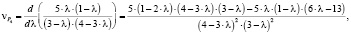 (36)
(36)
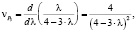 (37)
(37)
где 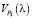 – скорости движения точки по графику P2(l);
– скорости движения точки по графику P2(l);
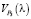 – скорости движения точки по графику P3(l);
– скорости движения точки по графику P3(l);
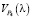 – скорости движения точки по графику P4(l);
– скорости движения точки по графику P4(l);
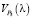 – скорости движения точки по графику P5(l).
– скорости движения точки по графику P5(l).
Результаты исследования и из обсуждение
Для количественной оценки и проведения дальнейших исследований построим графики зависимостей (29)–(33) скоростей перемещения точек по кривым (28), (30)–(33) от интенсивности потока. Пусть интенсивность потока изменяется с шагом 0,025 в интервале [0; 1]. Подставим в уравнения 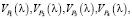 и
и 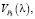 а результаты запишем в итоговую таблицу. И запишем результаты этих значений взятых по модулю.
а результаты запишем в итоговую таблицу. И запишем результаты этих значений взятых по модулю.
Используя данные таблицы, построим графики зависимостей 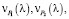
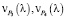 , и их модулей (рис. 4).
, и их модулей (рис. 4).
Результаты вычислений 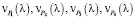 и их модулей
и их модулей
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
–4 |
2,5 |
0,833 |
0,416 |
0,25 |
4 |
2,5 |
0,833 |
0,416 |
0,25 |
|
0,025 |
–3,461 |
1,998 |
0,785 |
0,461 |
0,259 |
3,461 |
1,998 |
0,785 |
0,461 |
0,259 |
|
0,05 |
–3,024 |
1,596 |
0,738 |
0,501 |
0,269 |
3,024 |
1,596 |
0,738 |
0,501 |
0,269 |
|
0,075 |
–2,665 |
1,272 |
0,692 |
0,536 |
0,280 |
2,665 |
1,272 |
0,692 |
0,536 |
0,280 |
|
0,1 |
–2,366 |
1,006 |
0,647 |
0,566 |
0,292 |
2,366 |
1,006 |
0,647 |
0,566 |
0,292 |
|
0,125 |
–2,115 |
0,786 |
0,602 |
0,591 |
0,304 |
2,115 |
0,786 |
0,602 |
0,591 |
0,304 |
|
0,15 |
–1,902 |
0,604 |
0,559 |
0,609 |
0,317 |
1,902 |
0,604 |
0,559 |
0,609 |
0,317 |
|
0,175 |
–1,719 |
0,451 |
0,516 |
0,621 |
0,331 |
1,719 |
0,451 |
0,516 |
0,621 |
0,331 |
|
0,2 |
–1,562 |
0,322 |
0,474 |
0,627 |
0,346 |
1,562 |
0,322 |
0,474 |
0,627 |
0,346 |
|
0,225 |
–1,425 |
0,213 |
0,432 |
0,626 |
0,361 |
1,425 |
0,213 |
0,432 |
0,626 |
0,361 |
|
0,25 |
–1,306 |
0,120 |
0,391 |
0,617 |
0,378 |
1,306 |
0,120 |
0,391 |
0,617 |
0,378 |
|
0,275 |
–1,200 |
0,041 |
0,351 |
0,600 |
0,396 |
1,200 |
0,041 |
0,351 |
0,600 |
0,396 |
|
0,3 |
–1,108 |
–0,026 |
0,311 |
0,574 |
0,416 |
1,108 |
0,026 |
0,311 |
0,574 |
0,416 |
|
0,325 |
–1,025 |
–0,084 |
0,271 |
0,540 |
0,437 |
1,025 |
0,084 |
0,271 |
0,540 |
0,437 |
|
0,35 |
–0,951 |
–0,134 |
0,232 |
0,496 |
0,459 |
0,951 |
0,134 |
0,232 |
0,496 |
0,459 |
|
0,375 |
–0,885 |
–0,177 |
0,192 |
0,442 |
0,483 |
0,885 |
0,177 |
0,192 |
0,442 |
0,483 |
|
0,4 |
–0,826 |
–0,215 |
0,154 |
0,377 |
0,510 |
0,826 |
0,215 |
0,154 |
0,377 |
0,510 |
|
0,425 |
–0,772 |
–0,247 |
0,115 |
0,301 |
0,538 |
0,772 |
0,247 |
0,115 |
0,301 |
0,538 |
|
0,45 |
–0,724 |
–0,275 |
0,076 |
0,213 |
0,569 |
0,724 |
0,275 |
0,076 |
0,213 |
0,569 |
|
0,475 |
–0,680 |
–0,299 |
0,038 |
0,113 |
0,603 |
0,680 |
0,299 |
0,038 |
0,113 |
0,603 |
|
0,5 |
–0,64 |
–0,32 |
0 |
0 |
0,64 |
0,64 |
0,32 |
0 |
0 |
0,64 |
|
0,525 |
–0,603 |
–0,337 |
–0,038 |
–0,126 |
0,680 |
0,603 |
0,337 |
0,038 |
0,126 |
0,680 |
|
0,55 |
–0,569 |
–0,353 |
–0,076 |
–0,267 |
0,724 |
0,569 |
0,353 |
0,076 |
0,267 |
0,724 |
|
0,575 |
–0,538 |
–0,366 |
–0,115 |
–0,423 |
0,772 |
0,538 |
0,366 |
0,115 |
0,423 |
0,772 |
|
0,6 |
–0,510 |
–0,377 |
–0,154 |
–0,594 |
0,826 |
0,51 |
0,377 |
0,154 |
0,594 |
0,826 |
|
0,625 |
–0,483 |
–0,386 |
–0,192 |
–0,779 |
0,885 |
0,483 |
0,386 |
0,192 |
0,779 |
0,885 |
|
0,65 |
–0,459 |
–0,394 |
–0,232 |
–0,98 |
0,951 |
0,459 |
0,394 |
0,232 |
0,980 |
0,951 |
|
0,675 |
–0,437 |
–0,401 |
–0,271 |
–1,195 |
1,025 |
0,437 |
0,401 |
0,271 |
1,195 |
1,025 |
|
0,7 |
–0,416 |
–0,406 |
–0,311 |
–1,425 |
1,108 |
0,416 |
0,406 |
0,311 |
1,425 |
1,108 |
|
0,725 |
–0,396 |
–0,411 |
–0,351 |
–1,667 |
1,2 |
0,396 |
0,411 |
0,351 |
1,667 |
1,2 |
|
0,75 |
–0,378 |
–0,414 |
–0,391 |
–1,919 |
1,306 |
0,378 |
0,414 |
0,391 |
1,919 |
1,306 |
|
0,775 |
–0,361 |
–0,417 |
–0,432 |
–2,179 |
1,425 |
0,361 |
0,417 |
0,432 |
2,179 |
1,425 |
|
0,8 |
–0,346 |
–0,419 |
–0,474 |
–2,44 |
1,562 |
0,346 |
0,419 |
0,474 |
2,440 |
1,562 |
|
0,825 |
–0,331 |
–0,42 |
–0,516 |
–2,696 |
1,719 |
0,331 |
0,42 |
0,516 |
2,696 |
1,719 |
|
0,85 |
–0,317 |
–0,421 |
–0,559 |
–2,936 |
1,902 |
0,317 |
0,421 |
0,559 |
2,936 |
1,902 |
|
0,875 |
–0,304 |
–0,421 |
–0,602 |
–3,145 |
2,115 |
0,304 |
0,421 |
0,602 |
3,145 |
2,115 |
|
0,9 |
–0,292 |
–0,421 |
–0,647 |
–3,3 |
2,366 |
0,292 |
0,421 |
0,647 |
3,3 |
2,366 |
|
0,925 |
–0,280 |
–0,420 |
–0,692 |
–3,371 |
2,665 |
0,280 |
0,420 |
0,692 |
3,371 |
2,665 |
|
0,95 |
–0,269 |
–0,419 |
–0,738 |
–3,312 |
3,024 |
0,269 |
0,419 |
0,738 |
3,312 |
3,024 |
|
0,975 |
–0,259 |
–0,418 |
–0,785 |
–3,055 |
3,461 |
0,259 |
0,418 |
0,785 |
3,055 |
3,461 |
|
1 |
–0,25 |
–0,416 |
–0,833 |
–2,5 |
4 |
0,25 |
0,416 |
0,833 |
2,5 |
4 |
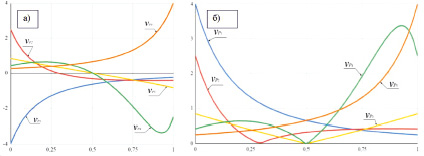
Рис. 4. Графики зависимостей а) 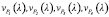 , б) значения взятые по модулю
, б) значения взятые по модулю
Выводы
1. Получены данные, необходимые для проведения первоначального грубого анализа систем управления процессами обработки информации, которые рассматриваются во времени и существуют на каждом этапе поискового исследования.
Получены графики зависимостей скорости перемещения рабочей точки, характеризующей поисковое исследование, по вероятностным характеристикам каждого этапа поискового исследования. Предложены:
– графическое изображение процесса движения точки по плоскостям в виде кривой fxz(t) на плоскости xz – вид сверху;
– графическое изображение перемещения точки по графикам зависимости P1(l), P2(l), P3(l), P4(l) и P5(l) на плоскости xy;
– графическое изображение перемещения точки по плоскости P1 в пространстве xyz рядом с финальной вероятностью P1(l).
Результаты исследования, если будут учтены при поэтапной оптимизации процесса поискового исследования, помогут разработчикам информационных систем и программного обеспечения достичь желаемой цели – снизить временные затраты на проведение поискового исследования. Для этого в теории статьи была учтена специфика поискового исследования, которое имеет дело с потоком научной информации и соответствующим образом обрабатывается на каждом этапе.
2. Получены данные, необходимые для определения показателей качества представления информации, используемой процессами обработки информации, которые рассматриваются во времени.
Были получены математические зависимости вероятности пребывания рабочей точки в текущем этапе поискового исследования:
– от времени выполнения процесса;
– полученных полезных знаний.
Авторы статьи предлагают обратить внимание на переменную – полезные знания для решения следующего этапа, полученные за время выполнения текущего. В дальнейших исследованиях будут использованы данные зависимости. По ним планируется построение плоскостей и их тщательный анализ.
Исследование проведено при финансовой поддержке РФФИ. Название проекта: «Развитие теории качественной оценки информации с учётом её структурной составляющей», № 19-47-230004, от 19.04.2019 г.
Библиографическая ссылка
Попова О.Б., Попов Б.К., Карандей В.Ю., Афанасьев В.Л. К ЗАДАЧЕ РАЗРАБОТКИ МЕТОДОЛОГИИ ОЦЕНКИ ВРЕМЕНИ ВЫПОЛНЕНИЯ ПОИСКОВОГО ИССЛЕДОВАНИЯ // Современные наукоемкие технологии. 2019. № 11-1. С. 88-96;URL: https://top-technologies.ru/ru/article/view?id=37771 (дата обращения: 08.03.2026).
DOI: https://doi.org/10.17513/snt.37771