Одним из эффективных и доступных инструментов исследования задач управления здравоохранением и медицинской организацией является моделирование. Используя модель, появляются возможности учесть влияние всех сколько-нибудь значимых факторов и их связей на результаты деятельности и своевременно принимать обоснованные управленческие решения. В настоящее время происходит всесторонняя интеграция медицины и информационных технологий, в связи с чем стало возможным использовать моделирование для всестороннего исследования процессов диагностики и лечения заболеваний [1].
Широкое применение в медицине и здравоохранении нашли кибернетические методы моделирования. Кибернетическая модель представляет собой систему, ориентированную на цель исследования. При этом ключевой особенностью моделей этого класса является возможность взаимоувязывания эндогенных и экзогенных переменных таким образом, как они связаны в исследуемом процессе. Полученные в результате модели процессов очевидным образом могут быть положены в основу программной имитационной системы.
В ходе ранее проведенных исследований была получена модель, иллюстрирующая процесс лечения пациента [2]. Однако само пространство состояний пациента в ходе лечения заболевания оставалось слабо формализованным.
Целью данного этапа исследования является разработка формализованного алгоритма методического обеспечения имитационной модели для исследования лечебно-диагностического процесса (ЛДП) медицинской организации.
Целевой установкой ЛДП может считаться достижение в ходе лечения некоторого целевого состояния [3]. В общем случае такими целевыми исходами могут считаться исходы, при которых пациент выздоравливает. А, по мнениям экспертов, в некоторых случаях удовлетворительными могут считаться состояния, связанные с ремиссией, хронизацией или стабилизацией.
Граф состояний пациента
В общем случае, пациент может поступить в медицинскую организацию в любом из xi ∈ X, i = 1…6 состояний степени тяжести заболевания. При этом, значение i = 1 означает «Болезнь отсутствует», а i = 6 – летальный исход. Промежуточные значения xi – тяжесть заболевания [1, 2].
Документами [3, 4] устанавливается процесс оказания медицинской помощи как некоторая совокупность этапов – маршрут, по мере прохождения которого пациент изменяет свое состояние. Таким образом, формируется технология лечения заболевания.
Развитие заболевания может происходить по-разному: сначала у пациента легкая степень тяжести, которая держится в течение некоторого времени; затем – средняя; далее – тяжелая, и т.д. Нередкими являются случаи быстрого развития заболевания – «скачкообразно», когда состояние здоровья ухудшается практически мгновенно (например, инфаркты, инсульты). Лечение заболевания – это всегда последовательный процесс, в ходе которого пациент как бы возвращается в состояние выздоровления. Указанные факты прогресса заболевания и его лечения положены в основу разрабатываемой модели. При этом целью лечения заболевания считается достижение целевого исхода, заключающегося в восстановлении здоровья пациента.
Состояние пациента si ∈ S, i = 1,…,n – это состояние, в котором он может находиться с вероятностью pi(si). При развитии заболевания происходит смена состояния: {pij(si → sj): si, sj ∈ S, i, j = 1,…,n; i < j}. При выздоровлении модель изменения состояния пациента имеет вид: {pji(sj > si): si, sj ∈ S, i, j = 1,…,n; j < i}.
В самом общем случае, n = 6 (болезнь отсутствует, легкое заболевание, заболевание средней тяжести, тяжелое заболевание, крайне тяжелое заболевание, летальный исход), тогда матрица переходов Р имеет вид
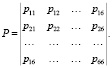(1)
Главная диагональ матрицы Р – некоторое состояние пациента. Вероятности справа – это вероятности, соответствующие ухудшению состояния здоровья, а слева – улучшения здоровья в ходе лечения. При этом, исходя из ранее обоснованного предположения о последовательном процессе выздоровления, вероятности p31,…, p51, p42,…, p52, p53, могут быть исключены из рассмотрения. А вероятности летального исхода p61,…, p66 – не имеет смысл рассматривать.
Поэтому матрицу Р можно записать следующим образом:
(2)
Таким образом, пространство состояний пациента иллюстрируется маркированным мультиграфом (рис. 1), в котором вершины – это состояния пациента, а дуги могут быть следующих типов:
– α – если есть переход из si в sj (развитие заболевания; показаны сплошными линиями);
– β – если имеет место переход из sj в si (лечение; пунктирная линия);
– ε – случай стабилизации состояния пациента, sii.
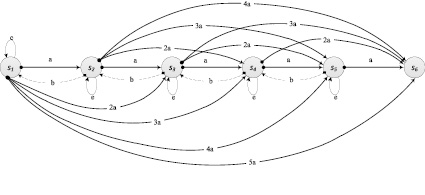
Мультиграф пространства состояний пациента
Рассмотрим пары состояний; s1 и s2, для которых pα+ pβ = 1. Но при этом не исключаются переходы вида s1 → s3. В этом случае имеет место 2pα + 2pβ = 1. Анализ возможных конфигураций маршрутов состояний пациента позволяет записать
(n – 1)pα + (n – 2)pβ = 1.
Для случая sii, pi(si) = pε.
Анализ рассматриваемой предметной области показывает, что развитие заболевания может развиваться как непрерывно, так и дискретно (резкое ухудшение здоровья). Причем заранее предсказать, в каком направлении и с какой интенсивностью будут происходить смены состояний пациента возможно только с некоторой долей вероятности. Что касается лечения заболевания, то это преимущественно непрерывный процесс, однако даже при заметном улучшении состояния здоровья возможны осложнения или иные непредвиденные ситуации. Приведенные рассуждения позволяют сделать вывод о дискретно-непрерывном и стохастическом характере рассматриваемого процесса. В данной модели намеренно не учитываются временные характеристики нахождения пациента в том или ином состоянии, поскольку для каждого заболевания имеется явная специфика лечения, а следовательно, и параметр времени будет специфичным. Это несколько упрощает модель, но при этом не теряются значимые для достижения цели исследования особенности.
Моделирование пространства состояний пациента
Как показано в [5], одной из лучших схем моделирования дискретно-стохастических систем является Р-схема, или вероятностный автомат.
Конечный стохастический автомат As представляет собой пятерку
AS = {X, Y, P, ρ0, F}, (3)
где x = {α, β, ε}; y = {y1, …, y6}; ρ0 = ||1,0,0,0,0,0||, F = {y1}; ρF = ||1,0,0,0,0,0||; Р = {Р(α), Р(β), Р(ε)}:
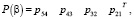
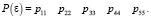
Представленные матрицы интерпретируются следующим образом:
P(α) – модель ухудшения состояния пациента;
P(β) – матрица выздоровления;
P(ε) – матрица отсутствия изменений.
Автомат, представленный (3), моделирует язык вида
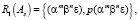
где m = k, n = k – 1,
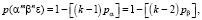
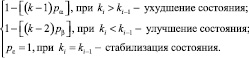
Язык R1(As) стохастического автомата получается путем порождения цепочек символов из алфавита этого языка. Синтез цепочек R1(As) основывается на формальной грамматике с дополнительной рандомизацией выбора продукций [6]. Тогда, следующая пятерка является стохастической грамматикой:
GS = (XT, XN, PS, S0, p0),
где ХТ – терминальный словарь (словарь, включающий символы разметки автомата As);
XN – нетерминальный словарь (содержит вспомогательные символы, используемые для вывода цепочек языка);
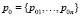– вероятностное распределение начальных символов из 
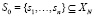, при этом 
, 
;
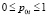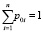PS – конечное множество вероятностных продукций, каждая из которых имеет вид
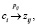
i = 1, …, k – число различных выводов цепочек с из символов si, j = 1, …, n – число начальных символов, pij – вероятность данной продукции, т.е. число, удовлетворяющее следующим условиям:
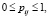
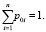
Если продукция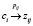 
принадлежит множеству PS, то считается, что цепочка g1 сi g2 непосредственно порождает цепочку g1 zij g2:
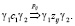
Цепочка g0 порождает цепочку gn, если существует такая последовательность g0, g1, …, gn, что
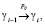i = 1, …, n.
Вероятностью такого порождения может считаться число
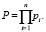
Если g0 порождает gn с вероятностью p, то это записывается следующим образом:
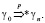
Грамматикой GS, порождается стохастический язык R(GS), представляющий собой множество пар:
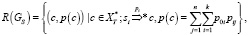
i = 1,…, k; j = 1,…,n,
где p0i – вероятность появления i-го начального символа;
pij – вероятность j-го вывода цепочки с из символа si.
Приведенные формальные определения стохастической грамматики GS позволяют определить стохастический автомат AS матрицей переходов (2). При этом Стохастическая грамматика этого автомата записывается в виде
GS = (XT, XN, PS, S0, p0),
где XT = {α, β, ε}; XN = {S}; p0 = 1; S0 = {s}, а стохастические продукции имеют вид
; 
; 
.
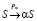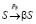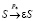Данная грамматика порождает язык:
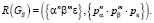
Пример [7].
Допустим, в медицинскую организацию поступает пациент в состоянии средней степени тяжести – s3. При использовании описанного подхода возможны следующие продукции:
; 
;
; 
;
; 
.
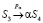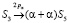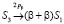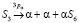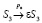При равновероятном распределении pa, pb имеет вид: pa = 0,5; pb = 0,5. Отсюда получим следующие результаты:
– цепочка c1 = ααα порождается с вероятностью: p(c1) = 0,53 = 0,125;
– цепочка c2 = ββ порождается с вероятностью: p(c2) = 0,25;
– цепочка c3 = αβββ порождается с вероятностью: p(c3) = 0,0625;
– цепочка c4 = ααββββ порождается с вероятностью: p(c4) = 0,03125.
Выбранные в данном примере значения pa и pb не являются результатом исследований. Значения выбраны произвольно только для демонстрации возможности использования предлагаемого подхода.
Заключение
При поступлении пациента в медицинскую организацию достаточно трудно предсказать, каким будет процесс его лечения и каким исходом он закончится. Проведенные в данной работе исследования показали, что вполне возможно формализовать связи между степенью тяжести заболевания и вероятностями исходов лечения. Причем по характеру эти связи являются функциональными. А значит, могут быть принятыми для оценки эффектов деятельности медицинской организации, например по показателю: «Доля достижения целевых исходов».
Кроме того, предлагаемый подход открывает возможности для разработки программной имитационной модели, с помощью которой могут быть набраны статистики для дальнейшего предсказательного моделирования процессов лечения. Очевидным развитием данного подхода является необходимость учета временного параметра в переходах состояний пациента.
Библиографическая ссылка
Горбачев Д.В., Кузнецов О.В. МОДЕЛЬ СТОХАСТИЧЕСКОГО АВТОМАТА ДЛЯ СИНТЕЗА ПРОДУКЦИЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ // Современные наукоемкие технологии. – 2019. – № 11-1. – С. 43-47;URL: https://top-technologies.ru/ru/article/view?id=37763 (дата обращения: 21.11.2024).