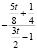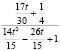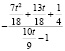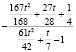Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Богомолова О.И. 1 Гараев Т.К. 2

---

1 Казанский государственный энергетический университет

2 Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ

В работе рассмотрена актуальная тема аппроксимации функции, обратной к функции гамма-распределения. Обратные функции могут быть использованы в математическом моделировании для решения уравнений и генерации ряда случайных чисел. В случае, когда функция является функцией вероятностного распределения, при генерации получают ряд, соответствующий необходимому вероятностному закону распределения. В работе рассматривается алгоритм и программная реализация получения аппроксимации Паде для функций, обратных к функциям распределения. Основой получаемой аппроксимации служит разложение Доминичи в ряд Тейлора, реализованное программно в математическом пакете Mathcad. Полученные коэффициенты разложения используются для аппроксимации Паде. Аппроксимация Паде – классический метод рациональной аппроксимации аналитических функций, заключающийся в представлении функции в виде отношения двух полиномов. Большой интерес к аппроксимациям Паде обусловлен широким применением рациональных приближений в задачах статистики, химии, механики, теоретической физики. Данный подход может быть использован для определенного вида функций, к которому относятся все функции распределения. Рассмотрен частный случай гамма-функции, для обратной к которой получена таблица Паде. Данные таблицы могут быть использованы для программной реализации на требуемом языке программирования. В работе проведен анализ относительных погрешностей полученных аппроксимаций.

Статья в формате PDF

0 KB

приближение функции

аппроксимация Паде

обратная функция

распределение вероятностей

гамма-функция

1. Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. БХВ-Петербург, 2014. 464 с.

2. Колдаев В.Д., Гагарина Л.Г. Численные методы и программирование. М.: Форум, 2018. 336 с.

3. Dominici D. The inverse of the cumulative standard normal probability function. Integral Transforms and Special Functions, 2003. № 4. С. 281–292.

4. Пантелеев А.В., Кудрявцева И.А. Численные методы для инженеров и экономистов. М.: Факториал Пресс, 2017. 416 c.

5. Богомолова О.И. Программная реализация разложения в ряд Тейлора функций, обратных к функциям распределения с использованием вложенных производных // Вестник Технологического университета. 2018. № 11. С. 119–122.

Один из важнейших разделов численной математики – аппроксимация функций [1]. Наиболее известный метод представления функции степенным рядом – разложение в ряд Тейлора [2]. В силу того, что нахождение приближения обратной функции представляет большую сложность, многие авторы исследовали эту проблему для конкретных функций, в частности для функции ошибок erf(x).

Цель работы: получить аппроксимацию функции, обратной к гамма-функции вероятностного распределения.

Материалы и методы исследования

Для обратных функций разложение в ряд Тейлора представляет сложность с точки зрения практического применения. Решению этой проблемы посвящены работы Доминичи [3]. Доминичи представляет алгоритм получения коэффициентов разложения обратной функции с использованием вложенных производных.

Разложение Доминичи для функций, обратных функциям распределения, обеспечивает высокую точность приближения не на всем рассматриваемом отрезке. Для обеспечения более высокой точности необходимо учесть в ряде Тейлора члены с более высокими степенями, что неизбежно приведет к увеличению времени вычисления аппроксимируемой функции. Для уменьшения степени разложения, без ухудшения точности приближения применим аппроксимацию Паде [2].

Аппроксимация Паде – классический метод рациональной аппроксимации аналитических функций, заключающийся в представлении функции в виде отношения двух полиномов. Большой интерес к аппроксимациям Паде обусловлен широким применением рациональных приближений в задачах статистики, химии, механики, теоретической физики и т.д. [4]. Аппроксимации Паде – это наилучшие рациональные аппроксимации заданного степенного ряда.

Результаты исследования и их обсуждение

Рассмотрим задачу получения таблицы Паде для обратной функции гамма-распределения. Для решения этой задачи потребуется получить коэффициенты разложения в ряд Тейлора для этой функции. Воспользуемся подходом, предложенным Доминичи. Автор рассматривает функции, задаваемые выражением

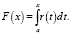(1)

Выражение (1) записывает функцию F(x), как несобственный интеграл, нижний предел которого a удовлетворяет условию a> = 0, верхний предел x условию –∞ < x < +∞. Частный случай функции F(x) – функция вероятностного распределения. Разложение базируется на введенном Доминичи понятии вложенной производной n-го порядка, которое определяется рекуррентно. Вложенная производная нулевого порядка определяется для f(x) = 1/r(x) выражением

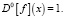(2)

Вложенная производная n-го порядка определяется выражением

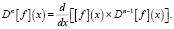(3)

Разложение в ряд Тейлора для функции, обратной функции распределения записывается выражением

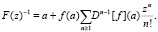(4)

В выражении (4) величиной a задаётся нижний предел интегрирования несобственного интеграла выражения (1), при условии f(a) ≠ 0; z – переменная, по которой производится разложение обратной функции. Запишем ниже программную реализацию разложения Доминичи, реализованную в математическом пакете Mathcad. Функция, разложение обратной к которой требуется найти, задается аналитически. Ниже показан код соответствующей программы [5]:

GetSeriesCoeff (N, h, x0)

с ← matrix (N +1,1,σ)

g(х) ←1

for n ∈1,2..N

g(x)←g'(x) + n•h(x)•g(x)

cn← g(х0)

return c

В коде программы используются следующие возможности математического пакета: аналитическое дифференцирование, матричная математика, циклы.

Функция, для обратной к которой требуется получить приближение, задается в Mathcad аналитически. Коэффициенты разложения этой функции в ряд Тейлора используются для получения коэффициентов аппроксимации Паде.

Аппроксимация Паде – рациональная дробь, в числителе которой многочлен степени L, а в знаменателе многочлен степени M:

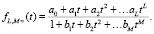(5)

В знаменателе присутствуют M + 1 слагаемых, в числителе L + 1 соответственно.

Таблица Паде представляет собой двумерный массив, в общем случае записываемый в виде

Таблица 1

Общий вид таблицы Паде

Первый столбец этой таблицы – частные суммы разложения в ряд Тейлора.

Вычисление коэффициентов ai аппроксимации Паде задается выражением

a0 = c0,

a1 = c1 + b1c0,

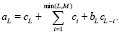(6)

Коэффициенты bi получаются программно, как решение системы линейных уравнений, записанных выражением

=

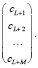- (7)

Алгоритм получения коэффициентов Паде в математическом пакете Mathcad можно представить последовательностью шагов:

1. Задать аналитически функцию, для обратной к которой требуется получить приближение.

2. Получить коэффициенты Доминичи разложения в ряд этой функции.

3. На основе полученных коэффициентов рассчитать коэффициенты Паде, используя выражения (5, 6) для различных значений N> = 1, M> = 1.

Используя предложенный алгоритм, решим задачу для получения аппроксимации Паде для функции, обратной функции гамма-распределения.

Плотность вероятности гамма распределения задается выражением

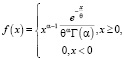(8)

Г(k) – гамма-функция Эйлера.

Гамма-распределение зависит от двух параметров и является абсолютно непрерывным. Это распределение получило широкое распространение в инженерных науках и экономических моделях. Гамма-распределение применяется для описания ряда величин, имеющих положительное значение. Данное распределение несимметрично. Коэффициент α является параметром формы, θ – параметром масштаба (рис. 1).

Получим аппроксимацию обратной к гамма-функции, выполняя алгоритм, описанный в работах Доминичи.

Первый этап – получение коэффициентов Dominici. Запишем в Mathcad функцию f(x) = 1/r(x):

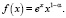(9)

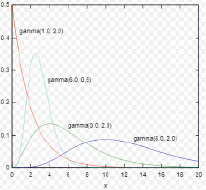
Рис. 1. Зависимость вида кривой гамма-распределения от параметров α и θ

Промежуточная величина h(x) = f’(x)/f(x) принимает значение 1 – (α – 1)/x. Значение α возьмем равным 0,5. Точке х0, в которой производим разложение функции присвоим значение равное 0,25. Для получения коэффициентов разложения в ряд Тейлора функции, обратной к гамма-функции, используем разработанную программную реализацию GetSeriesCoeff (N, h, x0) в математическом пакете Mathcad. Результат работы программы – вектор коэффициентов. Значения первых шести коэффициентов разложения, полученные программно: {1, 3, 10, 58, 424, 3928}.

Полученные коэффициенты используем для аппроксимации Паде, решая в Mathcad соответствующие системы уравнений (5, 6). На рис. 2 показан листинг программы в Mathcad, предназначенной для расчета коэффициентов аппроксимации Паде. В табл. 1 представлены аппроксимации Паде для значений M = 1,2 и значений N = 1,2.

Исследуем относительную погрешность аппроксимации Паде и Доминичи. Проведем сравнение полученных аппроксимаций с представлением функции в Mathcad. Значения обратной функции получим, поменяв значения аргумента и функции. На рис. 3 показан график относительной погрешности на отрезке [0,1] аппроксимации Паде и Доминичи. Четная степень аппроксимации Паде N означает, что в числителе и знаменателе стоят многочлены степени N/2. На графике видно, что общая степень N аппроксимации Паде обеспечивает на всем отрезке лучшую аппроксимацию, чем аппроксимация Доминичи (рис. 3).

Рис. 2. Листинг программы получения аппроксимации Паде

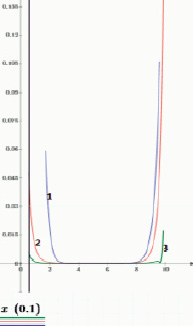
Рис. 3. Графики относительной погрешности для функции, обратной к функции гамма-распределения. Цифрами обозначены: 1 – приближение Доминичи (10-я степень); 2 – приближение Паде (8-я степень); 3 – приближение Паде (6-я степень)

Таблица 2

Таблица Паде для обратной к гамма-распределению функции (α = 0,5)

Заключение

Полученные в работе аппроксимации Паде для функции, обратной функции гамма-распределения, могут быть использованы в задачах численного моделирования. Коэффициенты аппроксимации Паде могут быть сохранены в текстовый файл и затем автоматически считаны для программной реализации на любом языке программирования. Полученные программы могут быть использованы для генерации ряда чисел, соответствующего гамма-распределению с заданными параметрами.

Библиографическая ссылка