Среди наиболее известных способов повышения использования ресурсов информационной сети автоматизированной системы специального назначения (АССН) известен способ под названием динамическое управление потоками информации, который позволяет минимизировать задержку при передаче пакетов [1, 2]. Разработанная процедура оптимизации управления передачей пакетов в информационной сети позволяет соседним с периодически недостижимым узлом информационной сети (с малым временем активности) распределять ресурсы таким образом, чтобы передать этому узлу наибольшее количество пакетов, адресованных ему. Аналогичная процедура может применяться и при недостижимости нескольких узлов информационной сети АССН.
Цель исследования: повышение эффективности управления целевыми информационными потоками от различных источников сообщений сети автоматизированной системы специального назначения достоверной и оперативной доставки сообщений.
Для решения поставленной задачи используется оптимизационный алгоритм на основе метода локально-оптимального поиска, использующий графы соседства в пространстве управления.
В АССН передача между двумя узлами обычно производится по нескольким путям, среди которых один принимается за основной, а остальные – за обходные. При этом на каждом узле задается перечень исходящих ветвей (направлений связи), которые можно использовать при передаче информации к каждому из остальных узлов информационной сети и порядок выбора этих ветвей [3, 4]. В терминологии построения информационных сетей АССН существует понятие – план распределения информации, который говорит о том, что для данного узла заданы состав допустимых исходящих направлений и порядок их выбора при установлении связи с любым из других узлов сети. Если такой план задан для каждого узла сети, то считается, что он задан для всей сети. Перечень допустимых исходящих направлений и порядок их выбора можно задать в виде матрицы маршрутов. Матрица маршрутов может быть задана как для собственного потока, т.е. потока поступающего от абонентов узла, так и для транзитных потоков, т.е. потоков, поступающих от других узлов сети. Если для каждого узла информационной сети заданы обобщенные матрицы маршрутов как для собственных, так и для транзитных информационных потоков, то они определяют планы как распределения информации, так и ограничения объема поступающей в сеть информации [2].
В имитационной модели (ИМ) пакет wj,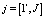 
, описывается набором признаков Pk, 
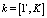, где K – количество признаков используемых в ИМ для описания пакетов, J – количество пакетов в сети [5]. Набор признаков pk, используемых для описания пакетов, будем называть характеристикой пакета и обозначим χ(wj):
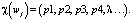
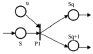
Символ λ в χ(wj) используется на месте тех признаков, которые не использовались для описания данного j-пакета. Признак pk принимают различные значения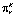 
, 
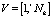, Nk – число различных значений k-го признака. Если зафиксировать некоторый набор значений признаков pk = χ(wj), то будет считать, что пакет wj пребывает в состоянии Sμ, 
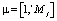, соответствующем этому зафиксированному набору значений pk, Mj – число значимых признаков j-го пакета. Очевидно, что 
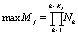, где Kj – число значимых признаков в χ(wj). Событие сопровождает переход из i-го состояния в другое. Соседние состояния различаются одним значением признака в χ(wj). Выбор набора признаков для описания пакетов и диапазона измерений их значений производится в зависимости от особенностей реальной проблемной области и требуемой степени подробности ее описания в модели сети АССН. На практике используется значительно меньшее число различимых состояний пакетов информационной сети, чем это дается оценкой maxMj. Происходит это потому, что не при каждом изменении значений признаков pk происходят действия над пакетами, а лишь при достижении этими признаками некоторых критических значений. Эти критические значения, определяющие переходы между различными состояниями, известны заблаговременно и могут контролироваться в ходе работы ИМ. В некоторых случаях существуют состояния в которых значения части признаков не принимаются во внимание. Признаки pk∈χ(wj), по значениям которых оценивается принадлежность wj тому или иному состоянию Sμ, будем называть характерными признаками μ-го состояния [5].
Присутствие пакета на маршруте wq будет представлять в ИМ как пребывание его в некотором состоянии Sμ. Признак, характеризующий временное и пространственное расстояние до вершины адресата, будет являться характерным признаком этого состояния. В вычислительных системах АССН отводится память для размещения характеристик пакетов χ(wi), находящихся в состоянии Sμ. Представлять это будем двояко:
1. wj∈Sμ
2. χ(wj)∈Mμ, где Mμ – массив памяти ЭВМ.
При этом в первом случае имя состояния Sμ становится именем подмножества пакетов wj находящихся в этом состоянии, во втором, Mμ считается именем подмножества характеристик χ(wj) записанных в нем. С учетом все этих представлений маршрут wq в ИМ представляется массивом Mμ, на котором определены 2 оператора: P1 и P2. P1 производит изменение во времени значений признаков в характеристиках χ(wj)∈Mμ. P2 контролирует значения характерных для μ-состояния признаков в характеристиках и исключает из Mμ те χ(wj), у которых характерные признаки достигли критического значения.
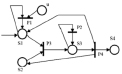
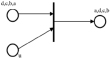
а) б)
Рис. 1. Варианты описания вершины Vi
В ИМ вершина Vi описывается достаточно разветвленной структурой, представляющей процесс многоканального и многофазного обслуживания пакетов (рис. 1).
Аппараты такого обслуживания будем представлять также наборами признаков, образующими характеристики узлов информационной сети:
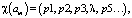
где am – имя m-го узла информационной сети,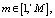 
M – число узлов сети, λ – используется на месте признаков, которые не применяются для описания данного узла информационной сети АССН.
В представленной на рис. 1 структуре вершины vi состояние S1 соответствует состоянию ожидания обслуживания. В S1 попадают все пакеты после завершения маршрута, для постановки в очередь на обслуживание. Управление пакетами в очереди производится приданием им различных приоритетов на обслуживание (т.е. выбор из очереди). Такое управление пакетами в очереди производится оператором P1 под действием управляющего элемента U задаваемого извне. Оператор P1 будем называть управляемым переходом перестановки. Используемый в ИМ управляемый переход – это операторы специального вида, реализуемые в виде программы со свободным полем памяти, которое заполняется извне перед каждым вариантом имитации процесса.
Свободные аппараты обслуживания находятся в состоянии S2. Выбор пакета из очереди (состояния S1) производится оператором P1. Одновременно с этим производится выбор свободного аппарата обслуживания пакетов. Обслуживание осуществляется оператором P2, определенным на множестве характеристик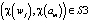 
, P2 изменяет во времени характерные признаки pk характеристик пакета и узла.
В случае достижения этими характерными признаками в состоянии S3 критических значений соответствующих характеристик χ(wj) и χ(am) пересылаются оператором P4:
- в состоянии S1, отсылаются характеристики пакета на следующую фазу обслуживания;
- в состоянии S2, отсылаются пакеты характеристики освободившихся узлов m;
- в состоянии S4 отсылаются характеристики пакетов, закончивших обслуживание и покидающих вершину vi.
Другая интерпретирующая структура представляет ветвление потока (рис. 1, б). Точки ветвления потока в модели информационной сети АССН являются точками управления. Допустим, известно, что через вершину vi, на которой происходит ветвление потока, за время T1 должно пройти n = n1 + n2 пакетов, где n1 – по маршруту w1 и n2 – по маршруту w2. Таким образом количество вариантов прохождения этой вершины пакетами будет равно n!/(n1!n2!) и будет отличаться направлениями адресации. Например, если n1 = 3 и n2 = 2, то варианты прохождения будут 11221, 22111, 12121, 21112 и т.д. Выбор того или иного варианта адресации пакетов, проходящих через точку ветвления, является управляющим воздействием на процесс перемещения пакетов в сети на интервале T1. В представленной структуре ветвления потока распределение характеристик пакетов, покидающих вершину vi, производится оператором P1, который является управляемым оператором и реализует задаваемый извне вариант распределения пакетов по маршрутам, будем называть его управляемым переходом (УП) ветвления.
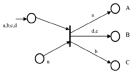
УП выполняющий функции выбора направления передачи называется УП первого рода (рис. 2, а), УП выполняющий функции выбора пакетов из очереди – УП второго рода (рис. 2, б). На представленных рис. 3 и 4 a, b, c, d – поток поступающих пакетов, Z(1) и Z(2) – вектора управляющего воздействия на переход, т.е. программа его работы. Вектор Z записывается перед каждым началом имитации. В нашем случае Z(1) состоит из номеров УПР адресатов, а Z(2) содержит приоритеты пакетов, согласно которым они выбираются из очереди.
Если определить заполнение всех узлов информационной сети, то можно получить матрицу управления Uf, строками которой является заполнение УП, элементы строки- номера узлов адресатов. Заполнением УП задается некоторая точка в пространстве оптимизации. Каждой такой точке ставится в соответствие матрица Uf.
Сформулируем задачу оптимизации:
1. Область поиска решения задается с помощью графа решения G(Uf). G(Uf) строится на множестве {Uf} матриц управления, F = [1, F], где F – мощность множества матриц управления.
2. Матрицы Uf являются вершинами графа G(Uf). Каждая вершина графа G(Uf) помечается значением оценочного функционала Lf, т.е. значением критерия достигаемого путем построения с помощью ИМ одного варианта имитации процесса при заданной Uf.
3. Имеется набор P правил p преобразования матриц Uf. Применение правил p к тем или иным матрицам не порождает новых матриц.
4. Цель управления формулируется в виде указаний: найти на графе G(Uf) вершину с экстремальным значением функционала Lf.
Правило p для УП первого типа имеет вид a→, b→, a←, b← и т.д., где стрелкой обозначено направление сдвига символов a, b в заполнении УП. Правило p для УП второго типа имеет вид: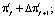 
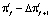, где πf – значение приоритета I-того пакета в f-той матрице управления, 
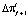– приращение приоритета при переходе к f + 1 матрице управления.
а) б)
Z(1) = (a(A), b(C), c(B), d(B)) Z(2) = (a(4), b(1), c(2), d(3))
Рис. 2. Варианты управляемого перехода
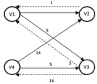
а) б)
Рис. 3. Пример оптимизационного алгоритма
Оптимизационный алгоритм является реализацией метода локально-оптимального поиска [6], использующего графы соседства в пространстве управления. Вершинами графов соседства служат матрицы управления Uf. На основе анализа решаемой задачи построение соседних матриц предлагается осуществить путем перемещения на N разрядов влево в строках матрицы Uf номеров узлов информационной сети, у которых время активности меньше по сравнению с другими. Можно ожидать, что при этом на сети будут создаваться условия, при которых пакеты, пересылаемые в данный узел информационной сети, будут адресоваться в нее раньше. Перемещая номера узлов информационной сети в строках матрицы управления на 1, 2, …, N разрядов влево, будем получать однососедние, двухсоседние, N – соседние матрицы управления. Идею этой процедуры рассмотрим на примере (рис. 3).
Среди вершин графа выделим подмножество вершин, передающих массив информации узлу информационной сети. На рис. 3, а это вершины V1 и V4, для них задается план передачи в числах пакетов Q(v1) и Q(v4). В частности, Q(v1) = 19, Q(v4) = 14. Окончанием процесса будем считать момент, когда будут переданы все пакеты. Определим конечную ситуацию, как на рис. 3, б, где горизонтальные линии соответствуют времени, в течении которого каждая из УПР ведет передачу. В качестве критерия оптимизации принимается minmaxTвп(Vi), где Tвп(Vi) момент выполнения плана I-м узлом информационной сети (момент окончания передачи узлом). Допустим, конечная ситуация, представленная на рис. 6, получена при матрице управления вида
При отстающей вершине V4 матрица U2, однососедняя к U1, имеет вид:
В U1 преобразованию подвергается строка ci, i = 3 путем смещения четверок на 1 разряд влево:
Таким образом, строка c3 будет иметь вид: 4 4 4 4 4 1 1 4 4 4 4 1 4 4 1 4 4 4 1.
Алгоритм оптимизации, построенный на основе предложенного способа построения соседних матриц управления, предполагает выполнение следующих этапов:
1. Выбирается случайная матрица управления U1сл.
2. С помощью ИМ строится вариант экстраполяции процесса при заданной U1сл до момента выполнения плана всеми УПР ПРС, для которых определен план.
3. Строится конечная ситуация вида рис. 6 и определяется отстающая вершина.
4. Осуществляется преобразование U1сл в целях получения однососедней матрицы по номеру отстающей вершины.
После этого идет переход к пункту 2 алгоритма. Алгоритм в цикле по пунктам 2–4 работает до тех пор, пока имеется тенденция к снижению критерия оптимизации. Показателем того, что возможности локальной оптимизации на базе случайной матрицы U1 исчерпаны, служат изменения знака приращений критерия оптимизации на последних этапах текущего шага оптимизации. После этого строится новая случайная матрица управления U1сл, и процесс оптимизации продолжается. Под этапом оптимизации понимается участок алгоритма, состоящий из пунктов 2–4. Шаг – это отрезок процедуры оптимизации между двумя соседними случайными матрицами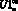 
управления. Работа алгоритма заканчивается либо по достижении целевой ситуации [6], т.е. такой, когда ∀vi, Tвп(vi) ≤ Tз, либо по истечении времени, отведенного для оптимизации.
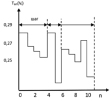
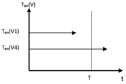
а)
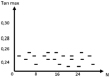
б)
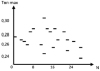
в)
Рис. 4. Поведение критерия оптимизации на шаге оптимизации и полученные результаты
Для рассматриваемого примера была построена и реализована ИМ, с помощью которой проведено исследование процесса перемещения пакетов на сети с точки зрения его оптимизации и определены характеристики эффективности предлагаемого алгоритма оптимизации. Для сопоставления эффективности описанного алгоритма оптимизации с методом случайного поиска [7] была проведена серия из 30 шагов (80 этапов) оптимизации. Характер поведения критерия оптимизации на шаге оптимизации показан на рис. 4, а.
На каждом шаге были выбраны лучшие достигнутые значения критерия (рис. 4, б) и проведено их сопоставление со значениями критерия, полученного при базовой (случайной) матрице управления на том же шаге (рис. 4, в).
Среднее значение критерия, достигнутое в результате оптимизации за 30 шагов, по сравнению со случайным поиском [7] уменьшилось на 8 % (с 0,278 до 0,255 мс), а дисперсия уменьшилась более чем в 3 раза. Среднее число этапов на одном шаге оптимизации оказалось равным 2,7. Лучшее значение критерия (T = 0,245 мс), достигнутое в результате оптимизации, меньше лучшего, найденного при случайном поиске на 5,3 %.
Заключение
Таким образом, предложенный метод повышения эффективности управления потоками в информационных сетях АССН показал свою достаточную эффективность и простоту применения, что позволит усовершенствовать существующие методы динамического управления потоками при наличии априорной информации о последующем изменении ситуации на сети.
Библиографическая ссылка
Цветков А.Ю., Самсонов Ф.А., Галанкин А.В., Прохоров М.А. РАЗРАБОТКА МЕТОДА ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ УПРАВЛЕНИЯ ИНФОРМАЦИОННЫМИ ПОТОКАМИ В СЕТЯХ АВТОМАТИЗИРОВАННЫХ СИСТЕМ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ С ПОМОЩЬЮ ИМИТАЦИОННОЙ МОДЕЛИ // Современные наукоемкие технологии. – 2019. – № 10-2. – С. 313-318;URL: https://top-technologies.ru/ru/article/view?id=37743 (дата обращения: 23.11.2024).