Оценка потерь времени на регулируемых пешеходных переходах является актуальной темой исследования в настоящее время. В силу увеличения интенсивности как транспортных, так и пешеходных потоков в городах количество регулируемых пересечений увеличивается и их влияние на суммарные затраты на передвижение транспорта и пешеходов также растет [1]. Как правило, среднее время на пересечение пешеходного перехода по различным методикам их вычисления складываается из времени ожидания возможности продолжить движение и времени, необходимого для непосредственного пересечения перехода. Методы расчета зависят от выбранного метода моделирования потоков транспорта и пешехода, а также от целей, для которых в дальнейшем будет применен данный аналитический инструмент.
Моделирование транспортных потоков развивается с середины прошлого столетия. Разработано большое количество моделей, разнообразных по степени детализации данных. В последнее время их классифицируют на макроскопические, мезоскопические и микроскопические. Пешеходным потокам внимание стали уделять значительно позже. Однако сейчас потребность в его моделировании существует в различных отраслях экономической и социальной политики. Прогнозирование поведения людей требуется при проведении массовых мероприятий, при строительстве зданий и сооружений для составления плана эвакуации людей в случае чрезвычайных ситуаций, при проектировании транспортной сети города, края или области для оптимизации перевозки пассажиров и грузов. В разных случаях требуется разная степень детализации и точности модели. Поэтому разработаны и продолжают разрабатываться модели пешеходных потоков, отвечающие тем или иным требованиям.
Актуальной задачей является разработка модели движения транспорта и пешеходов на регулируемом переходе, дающая результат приемлемой точности при минимально возможном количестве исходных данных, которые могут быть получены автоматизированно в режиме реального времени.
Цель работы: разработка метода сбора и обработки исходных данных для мезоскопической модели движения транспорта и пешеходов на регулируемом переходе, разработанной автором.
Материалы и методы исследования
Существующие модели пешеходных потоков можно ранжировать на макромодели, мезомодели и микромодели [2–4]. В случае направленного движения пешеходов к переходу удобно применять модели, описывающие поток как случайный процесс с помощью случайных функций. Такую степень детализации данных можно отнести к мезоскопической.
В модели TIMeR_Mod, разработанной автором [5], автотранспортный поток описывается как поток Пальма, интервалы по времени между которыми подчиняются обобщенному закону Эрланга. Это достаточно универсальное многопараметрическое статистическое распределение, которое при соответствующем подборе параметров позволяет описать потоки различной плотности. Однако полностью скопировать предположения, выдвинутые при моделировании транспортного потока, на поток пешеходный не представляется возможным.
Для получения исходных данных модели пешеходного перехода с вызывным устройством необходимо по результатам видеосъемки вычислить параметры пешеходного потока и транспортных потоков на каждой из полос для движения, прибывающих к переходу. С этой целью будем использовать методы статистического анализа, кластерный анализ.
Результаты исследования и их обсуждение
Описание модели движения пешеходного потока
Рассмотрим вызывное устройство, расположенное вблизи такого «источника» пешеходного потока, как остановка общественного транспорта, кинотеатр, учебное заведение и т.п. В этом случае потоки пешеходов состоят из кластеров, движущихся в данном направлении (рис. 1). Каждый кластер характеризуется тем, что достаточно одного нажатия кнопки вызывного утройства, чтобы все успели пересечь дорогу.
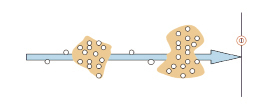
Рис. 1. Поток пешеходов к переходу с вызывным устройством
Поэтому целесообразно рассматривать такой поток не как поток отдельных пешеходов, а как поток кластеров. Считая поток распределенным по показательному закону, его интенсивность обозначим через 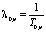 , где Т0p – средний интервал (в секундах) по времени между подряд идущими событиями (в нашем случае, между следующими друг за другом кластерами).
, где Т0p – средний интервал (в секундах) по времени между подряд идущими событиями (в нашем случае, между следующими друг за другом кластерами).
Кластерный анализ данных для моделирования пешеходного движения
Основная задача кластерного анализа – разбить множество объектов на классы, однородность которых определяется по некоторым заданным признакам. Это многомерный статистический метод, который позволяет работать с данными значительного объема и учитывать одновременно несколько n признаков, характеризующих объекты [6]. Объекты представляют как точки в n-мерном пространстве, а однородность определяют по расстоянию между этими точками. Расстояние в общем случае можно вводить разными способами, главное, правильно подобрать масштаб по каждой из осей. С этой целью нормируют данные. В качестве расстояния можно выбрать, например, линейное, евклидово, квадрат евклидова расстояния, обобщенное степенное расстояние Минковского, расстояние Чебышева, Манхэттенское расстояние. Методы разбиения на кластеры классифицируют как иерархические и неиерархические.
Основные этапы кластерного анализа следующие: формулировка проблемы; выбор способа измерения расстояния; выбор места кластеризации; принятие решения о количестве кластеров; интерпретация и профилирование кластеров; оценка достоверности кластеризации [7].
Для разделения пешеходов на кластеры будем использовать иерархическую агломеративную процедуру, последовательно объединяя пешеходов в отдельные группы. Основной признак, по которому будем объединять объекты – расстояние между соседними пешеходами и расстояние до центра кластера. Кроме того, введем ограничение Dmax на диаметр кластера и Dfree на расстояние между соседними объектами. Константу Dmax определяют при калибровке модели к конкретному переходу. Она определяется из условия гарантированного перехода через дорогу всех объектов в кластере за один цикл при известных параметрах: средней скорости отдельного пешехода и ширине проезжей части. Константа Dfree определяет движение пешехода вне кластера.
Возможны два подхода к автоматизированному сбору данных. В первом случае в данный момент времени снимаются показания с видеодетектора о месторасположении объектов и фиксируются их декартовы координаты на плоскости Oxy: (xi, yi). Тогда расстояние между двумя объектами dij находим как обычное Евклидово расстояние:
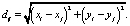 (1)
(1)
Объекты объединяются в один кластер, если расстояние от объекта до центра кластера не превышает 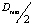 , и внутри круга радиусом Dfree находится хотя бы один объект формируемого кластера. При добавлении нового объекта в кластер пересчитывается диаметр и центр кластера. Диаметр dc – это расстояние между двумя наиболее удаленными объектами, а центр – координаты середины диаметра.
, и внутри круга радиусом Dfree находится хотя бы один объект формируемого кластера. При добавлении нового объекта в кластер пересчитывается диаметр и центр кластера. Диаметр dc – это расстояние между двумя наиболее удаленными объектами, а центр – координаты середины диаметра.
Во втором случае для каждого момента времени снимается только координата xi, отражающая проекцию объекта на ось направления движения. Тогда расстояние dij между двумя объектами равно
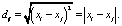 (2)
(2)
Диаметр в данном случае равен наибольшему расстоянию между проекциями объектов на ось направления движения (рис. 2).
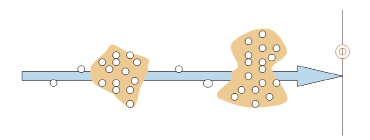
Рис. 2. Диаметр кластеров при моделировании пешеходного потока
При моделировании движения на подходах к пешеходному переходу задействуется для снятия показаний небольшой участок,который можно аппроксимировть прямой линией. В противном случае, если направление движения представляет собой кривую линию и аппроксимация ее прямой нерациональна, тогда в качестве координат берут проекции точек на кривую. Расстояние dij рассчитывается как длина дуги кривой, на которую проецируются точки.
В условиях данной модели второй случай формирования кластеров предпочтительнее. Исходя из поведения пешеходов, важна их удаленность от перехода вдоль направления движения. Пешеходы, выстроившиеся в «узкий», но «широкий» кластер, начинают движение по переходу одновременно.
Алгоритм обработки данных для пешеходного потока
Плотность распределения показательного закона распределения случайной величины имеет вид
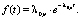 (3)
(3)
Он является однопараметрическим и применим для потоков с небольшой интенсивностью [8]. При разбиении пешеходного потока на кластеры мы можем им воспользоваться. Для получения значения параметра λ0p показательного закона требуется по экспериментальным данным определить средний интервал по времени между подряд идущими событиями Т0p. Тогда 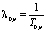 .
.
При организации эксперимента необходимо получить следующие измерения: интервалы по времени 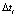 между последовательными прибытиями центров кластеров пешеходного потока к данной точке пространства на подходах к пешеходному переходу. Тогда выборочное среднее:
между последовательными прибытиями центров кластеров пешеходного потока к данной точке пространства на подходах к пешеходному переходу. Тогда выборочное среднее:
 (4)
(4)
где n – количество измерений, а 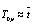 .
.
Алгоритм обработки данных для пешеходного потока:
1) в момент времени s = t1 фиксируем координаты xi проекций точек (пешеходов) на ось направления движения;
2) проводим разбиение на кластеры (рис. 3):
2.1) располагаем точки по возрастанию координат xi;
2.2) вычисляем расстояние от точки x* = xN с наибольшей координатой до соседней;
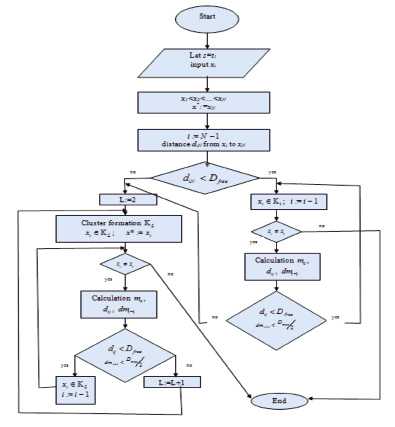
Рис. 3. Алгоритм формирования кластеров пешеходного потока в определенный момент времени
2.3) если расстояние 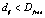 , объединяем точки в один кластер;
, объединяем точки в один кластер;
2.4) находим центр кластера mc как середину отрезка между точками;
2.5) находим расстояние dij от последней включенной в кластер точки xi до следующей по убыванию xi–1 и расстояние dmi–1 от точки xi–1 до центра кластера mc;
2.6) если оба условия 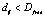 и
и 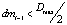 выполнены, включаем точку xi–1 в текущий кластер;
выполнены, включаем точку xi–1 в текущий кластер;
2.7) находим центр кластера как середину отрезка между xi–1 и x*: 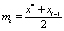 ;
;
2.8) если хотя бы одно из условий пункта 2.6 текущего алгоритма не выполнено, включаем точку xi–1 в новый кластер и считаем для нового кластера 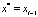 ;
;
2.9) повторяем пункты 2.5–2.8 до тех пор, пока все данные для момента времени s = 1 не будут разбиты на кластеры;
3) фиксируем координату центра первого кластера на оси направления движения Xcontrol;
4) фиксируем момент времени s = t2, когда центр второго кластера достигает точки Xcontrol;
5) вычисляем 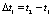 ;
;
6) повторяем пункты 2–5 для момента времени s = t2 необходимое количество n раз;
7) вычисляем 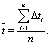
Получение и обработка данных для автотранспортного потока
Определение параметров распределения Эрланга для автотранспортного потока подробно описано, например, в работе автора [5]. Для их расчета необходимо получить экспериментальные данные о величине интервалов по времени между подряд идущими транспортными средствами в потоке, фиксируя их прибытие к данной точке дороги. Распределение Эрланга является многопараметрическим. Для получения оценки этих параметров по данным эксперимента рассчитываются 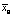 – выборочная средняя случайной величины T – интервалов между следующими подряд по одной полосе автомобилями;
– выборочная средняя случайной величины T – интервалов между следующими подряд по одной полосе автомобилями; 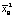 – выборочная средняя случайной величины T;
– выборочная средняя случайной величины T; 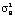 – выборочная дисперсия случайной величины T.
– выборочная дисперсия случайной величины T.
В первую очередь вычисляется значение 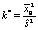 и находится ближайшее целое число, большее k*:
и находится ближайшее целое число, большее k*:
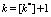 . (5)
. (5)
Экспериментально доказано, что начение параметра k не превышает четырех.
Считая, что 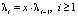 , остальные значения параметров распределения были рассчитаны с помощью метода моментов.
, остальные значения параметров распределения были рассчитаны с помощью метода моментов.
При k = 1 получем показательный закон, для которого 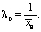
При k = 2:
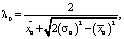
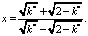 (6)
(6)
При k = 3:
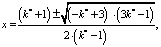
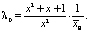 (7)
(7)
При k = 4:
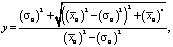
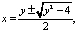
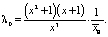 (8)
(8)
Замечание: если 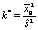 – целое число, то для всех
– целое число, то для всех 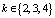 получим значение x = 1, а следовательно, все λi совпадают. В этом случае получим специальное распределение Эрланга или, иначе, «распределение Эрланга». Тогда параметры распределения находятся по следующим формулам:
получим значение x = 1, а следовательно, все λi совпадают. В этом случае получим специальное распределение Эрланга или, иначе, «распределение Эрланга». Тогда параметры распределения находятся по следующим формулам:
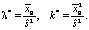 (9)
(9)
Заключение
Разработанная автором модель движения автомобильного транспорта и пешеходов через регулируемое пересечение требует исходных данных, которые возможно снимать и обновлять автоматизированно с помощью видеодетекторов. Развитие компьютерных и информационных технологий делает возможным обновление этих данных в режиме онлайн. Этот факт позволяет использовать разработанную мезоскопическую модель в Интеллектуальных транспортных системах для прогнозирования изменения задержек пешеходов и автотранспорта с течением времени.
Библиографическая ссылка
Наумова Н.А. АЛГОРИТМ ОПРЕДЕЛЕНИЯ ИСХОДНЫХ ДАННЫХ ДЛЯ МОДЕЛИРОВАНИЯ ПЕШЕХОДНОГО ПЕРЕХОДА С ВЫЗЫВНЫМ УСТРОЙСТВОМ // Современные наукоемкие технологии. 2019. № 10-2. С. 285-289;URL: https://top-technologies.ru/ru/article/view?id=37738 (дата обращения: 21.02.2026).



