Научный журнал

Современные наукоемкие технологии

ISSN 1812-7320

"Перечень" ВАК

ИФ РИНЦ = 0,940

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Медведев А.В. 1 Победаш П.Н. 2 Рапп Е.Ю. 1 Крамаренко В.А. 2

---

1 ФГБОУ ВО «Российский экономический университет имени Г.В. Плеханова» Кемеровский институт (филиал)

2 ФГБОУ ВО «Кузбасский государственный технический университет имени Т.Ф. Горбачева»

В статье приводится описание финансово-аналитического программного продукта, в основе которого лежит решение линейной задачи оптимального управления в дискретном времени. Кратко изложена концепция моделирования экономических процессов и математический инструментарий для решения задач указанного класса в целях экономического планирования и прогнозирования. Подчеркнута необходимость использования при описании и оценке эффективности деятельности предприятия комбинации оптимизационного подхода, выявляющего ее экономический потенциал, с имитационным, максимально учитывающим правила формирования возникающих доходных и расходных потоков. Рассмотрена общая математическая постановка многошаговой задачи линейного программирования, а также имеющие экономический смысл условия существования решения во всех допустимых диапазонах входящих в нее переменных и параметров. Приведен алгоритм преобразования исходной задачи в эквивалентную ей задачу линейного программирования. Кратко описаны вычислительные характеристики программного продукта, технология построения информационных услуг, а также ряд особенностей работы разработанного автоматизированного программного комплекса. Представлены результаты модельного вычислительного эксперимента с использованием входной информации, соответствующей реальному инвестиционному проекту регионального уровня, а также графоаналитический метод визуализации его результатов. Предложенный инструментарий можно рассматривать как систему поддержки принятия инвестиционных, производственных и финансовых решений как на микро-, так и на мезоэкономическом уровне при стратегическом планировании деятельности различных экономических структур.

Статья в формате PDF

0 KB

стратегическое экономическое планирование и прогнозирование

многошаговая задача линейного программирования

пакет прикладных программ

автоматизированная система поддержки принятия решений

1. Гурман В.И., Матвеев Г.А., Трушкова Е.А. Социо-эколого-экономическая модель региона в параллельных вычислениях // Управление большими системами: сборник трудов. 2011. № 32. С. 109–130.

2. Горбунов М.А., Медведев А.В., Победаш П.Н., Смольянинов А.В. Оптимизационный пакет прикладных программ «Карма» и его применение в задачах бизнес-планирования // Фундаментальные исследования. 2015. № 4. С. 42–47.

3. Габасов Р., Кириллова Ф.М. О некоторых проблемах оптимального управления в реальном времени линейными стационарными системами // Известия Иркутского государственного университета. Серия «Математика». 2019. Т. 27. С. 15–27.

4. Апалькова Т.Г., Мищенко А.В. Методы и модели оценки эффективности управления производственно-финансовой деятельностью в промышленной логистике // Логистика и управление цепями поставок. 2016. № 2 (73). С. 8–27.

5. Целых А.Н., Целых Л.А., Стаханов Д.В. Система поддержки принятия инвестиционных решений в малом бизнесе // Известия ЮФУ. Технические науки. 2013. № 6 (143). С. 166–173.

6. Программа для решения многошаговой задачи линейного программирования методом последовательных приближений («Линейная динамика») / Программа для ЭВМ. Свидетельство о регистрации в Роспатенте № 2004611491 от 17.06.2004. Правообладатели: А.В. Медведев, П.Н. Победаш.

Описание функционирования экономических систем требует учета множества сложных процессов в экономике – инвестиционных, производственных, финансовых, управленческих, – и поэтому затруднительно без разработки их математических моделей. Кроме того, цифровые технологии автоматизированной обработки циркулирующих в этих моделях материальных, финансовых и информационных потоков должны иметь реализуемые на компьютере алгоритмы и позволять как получать искомое решение моделируемых задач, так и анализировать его в удобной для конечного пользователя форме. При изучении экономических процессов в первую очередь интерес представляют модели динамических задач, характеризующиеся наличием временной переменной и зависимостью от нее других искомых переменных и параметров. Большинство современных автоматизированных программных систем, ориентированных на решение планово-прогнозных задач экономики, в качестве своей математической основы имеют задачу Коши для системы обыкновенных линейных дифференциальных уравнений 1-го порядка, имитирующие развитие предприятия. Получаемые решения описывают траекторию развития предприятия во времени, имитируя тем самым различные стороны его функционирования. Однако, не решая задачу оптимального управления, они не позволяют определять объемы инвестиций, производства продукции и соответствующие показатели финансово-хозяйственной деятельности предприятия, выявляющие наилучшие (в смысле выбранных критериев) варианты развития. С другой стороны, имеющиеся оптимизационные пакеты опираются на модели, описывающие преобразование затрат в выгоды производственными функциями абстрактно-математического характера (типа функций Кобба – Дугласа в модели Р. Солоу), что излишне идеализирует деятельность предприятия, либо (например, [1]) труднодоступны для конечного пользователя или громоздки в использовании, что, как правило, не удовлетворяет целевую аудиторию конечных пользователей данных пакетов.

В связи с изложенным выше, для решения задач экономического планирования и прогнозирования, на наш взгляд, целесообразно ориентироваться на комбинацию имитационных и оптимизационных методов, суть которых можно сформулировать следующим образом. Необходимо разрабатывать автоматизированные финансово-аналитические системы, в основе которых лежат оптимизационные модели деятельности предприятия, а потоки доходов и расходов в них формируются путем применения универсальных бухгалтерских алгоритмов (то есть, по возможности, использовать максимальную информацию о циркулирующих в экономической системе потоках). При этом полный компьютерный анализ инвестиционной, производственной и финансовой деятельности предприятия должен быть доступен для всех указанных составляющих. Иначе говоря, содержательная адекватность описания деятельности предприятия должна соответствовать используемым классам математических моделей и возможностям их полного компьютерного анализа. Обоснование указанных положений можно рассматривать в качестве цели данного исследования.

Материалы и методы исследования

Для реализации предлагаемого подхода целесообразно использовать удовлетворяющую указанным выше требованиям многошаговую задачу линейного программирования (МЗЛП): найти такие векторы u(t) и x(t), что справедливы условия

x(t + 1) = A(t)x(t) + B(t)u(t) – s(t); x(0) = a,

C(t)x(t) + D(t)u(t) ≤ h(t); u(t) ≥ 0 (t = 0,..., T0 – 1), (1)

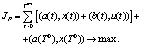
Здесь u(t) = [ul(t)], x(t) = [xi(t)] – управляющий и фазовый векторы соответственно; матрицы A(t) = [aij(t)]; B(t) = [bil(t)]; C(t) = [ckj(t)]; D(t) = [dkl(t)]; векторы a = [ai]; s(t) = [si(t)]; h(t) = [hk(t)]; a(t) = [ai(t)]; b(t) = [bl(t)]; (i, j = 1,... n; l = 1,... rt; k = 1,... mt; t = 0,…,T0); rt, mt и T0 – размерность вектора u(t), число неравенств в момент времени t и шагов по времени соответственно; (α, β) – скалярное произведение векторов α и β. Матрицы задачи (1) могут содержать практически неограниченную информацию об описываемых инвестиционных, производственных и финансовых процессах, в том числе имеющих нелинейный по переменной t характер. При этом, являясь линейной по фазовым и управляющим векторам, задача (1) может быть решена на основе эффективных численных алгоритмов при практически значимых размерностях rt, mt и T0, выявляя экономический потенциал инвестиционных, производственных и финансовых процессов.

Интерес к исследованию класса систем вида (1) в настоящее время не ослабевает [1–3], что обусловлено, с одной стороны, их важной содержательной составляющей, связанной с необходимостью изучения реальных технических и экономических процессов, описываемых в классе МЗЛП, а с другой, – с возможностями их автоматизированного компьютерного решения и анализа. Следует отметить, что аналитическое решение многошаговой задачи (1) в общей постановке не получено. Кроме того, при больших значениях n, T0 затруднительно получение и ее численного решения, а имеющиеся пакеты программ, в которых задача (1) решается в частном случае отсутствия, например, фазовых ограничений (С(t) = 0, t = 0,…,T0), резко ограничивают круг ее реальных экономических приложений. Поэтому вопросы разработки автоматизированных средств решения и анализа указанных систем также остаются в центре внимания исследователей [4, 5].

Известно, что при разработке автоматизированных средств численного решения задач вида (1) крайне важно знать заранее, всегда ли существует такое решение. В [2] приведен библиографический список работ, в которых теоретически и численно обосновано, что при выполнении условий

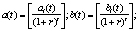
i = 1,…,n; t = 0,…,T0 – 1, (2)

задача (1) имеет решение во всех диапазонах изменения входящих в нее параметров и допустимых значений искомых управляющих u(t) и фазовых x(t) переменных. В этой связи автоматизация анализа задачи (1)–(2) приобретает очевидный смысл. Следует отметить, что условия (2) описывают известный в экономических приложениях процесс дисконтирования денежных потоков во времени, моделирующий всеобщий экономический закон обесценения во времени стоимости финансового ресурса. Это обуславливает целесообразность применения системы (1)–(2) именно и в первую очередь при анализе финансово-экономических процессов развития экономических систем. Однако последнее не исключает применение задачи (1)–(2) и пакетов ее автоматизированного анализа в технических приложениях, особенно если техническая система характеризуется целевыми функционалами, учитывающими объективно существующие законы трения в системе. Задача (1)–(2), как многошаговая задача линейного программирования, может быть решена путем перехода к эквивалентной ей статической ЗЛП путем следующих рассуждений.

Выражая фазовый вектор x(t) через управляющий вектор u(t) из уравнений движения в (1), получим

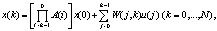
где ,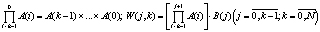

N – количество шагов. В этом случае МЗЛП вида

x(k + 1) = A(k)x(k) + B(k)u(k) 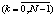; x(0) = a,

C(k)x(k) + D(k)u(k) ≤ h(k); u(k) ≥ 0 ,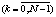

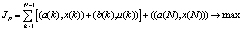
сводится к статической ЗЛП:

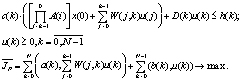(3)

Причем

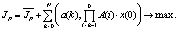
Результаты исследования и их обсуждение

Для автоматизированного анализа задачи (1)–(2) на основе алгоритма (3) был разработан комплекс прикладных программ [6]. В [2] приведена библиография источников, содержащих модели задач управления экономическими процессами и системами вида (1)–(2), а также результаты соответствующих вычислительных экспериментов, успешно подтверждающих существование их решения и позволяющих получать полезные для практики социально-экономических исследований результаты. Вместе с тем пакет [6] реализован на языке Паскаль, что затрудняет разработку соответствующих современным вычислительным и аналитическим возможностям систем поддержки принятия решений при анализе задачи (1)–(2). Данный факт предопределил необходимость дальнейшего совершенствования указанного программного комплекса в объектно-ориентированных программных средах, что привело к разработке авторами описанной ниже автоматизированной информационной системы «Линейная экономическая динамика» (АИС «ЛЭД») в объектно-ориентированной среде Microsoft Visual Studio на алгоритмическом языке C#.

Автоматизированная информационная система «ЛЭД» имеет две основные функции поддержки принятия решений при анализе задачи (1)–(2):

1) внесение и верификация входной матрично-числовой информации;

2) получение и анализ оптимального решения задачи u*(t), x*(t) (t = 0,…,T0) в форме одно- и многопараметрических зависимостей.

Разработанный комплекс не требователен к ресурсам компьютера, однако для комфортной работы необходимо наличие следующих программно-технических средств и ресурсов, представленных в табл. 1.

Использование АИС «ЛЭД» ориентировано на различных пользователей. Специалисту-математику она позволяет заносить матрично-числовую информацию и корректировать математические модели в форме (1)–(2), а также контролировать корректность внесения информации, а конечному пользователю – экономисту-аналитику – в удобном режиме создавать собственную конфигурацию бизнес-проектов (выделяя блоки характеристик активов, продукции, внешнего окружения проекта, финансовый блок и т.п.) и заносить входную статистическую и экспертную информацию. Указанные свойства, по сути, превращают АИС «ЛЭД» в систему поддержки принятия инвестиционных, производственных и финансовых решений. Основным аналитическим инструментом АИС «ЛЭД» является блок анализа графической информации, позволяющий представлять результаты расчетов в виде совокупностей графиков многопараметрических зависимостей, одновременно получаемых на нескольких графических полях (от одного до девяти). Тестирование АИС «ЛЭД» проводилось при различных размерностях n, T0. Используемая версия симплекс-метода давала устойчивые расчеты в следующих максимальных диапазонах их значений: 1) n = 1÷2, T⁰ ≤ 100; 2) n = 3÷5, T⁰ ≤ 30; 3) n ≥ 6, T⁰ ≤ 10, что позволяло решать большинство прикладных задач экономического анализа реальных инвестиционно-производственных проектов. При этом длительность самых объемных расчетов не превышала нескольких секунд.

Для краткой иллюстрации работы АИС «ЛЭД» рассмотрим численный эксперимент с представленными в табл. 2 входными параметрами модели развития некоторой региональной экономической системы.

Таблица 1

Программно-технические требования к использованию АИС «ЛЭД»

Таблица 2

Параметры инвестиционного проекта

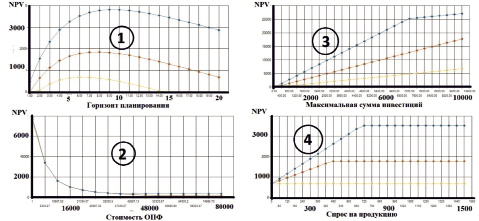
Графики зависимостей NPV от горизонта планирования (1), стоимости ОПФ (2), максимальной суммы инвестиций (3) и спроса на продукцию (4) при варьировании параметра стоимости ОПФ (оптимистический, базовый и пессимистический сценарии)

На рисунке представлены серии графиков, полученных в среде АИС «ЛЭД», отражающих чистую приведенную стоимость (NPV) проекта в зависимости от интересующих исследователя параметров. Приведенные группы графиков, отражаемых одновременно на четырех независимых графических полях (максимальное количество графических полей в системе – девять), в частности, иллюстрируют зависимости NPV от ряда ключевых параметров инвестиционного проекта при варьировании некоторого, заранее выбранного параметра (в данном случае, стоимости комплекта ОПФ).

АИС «ЛЭД», наряду с пакетом [6], используется при расчете ряда инвестиционных проектов стратегического планирования [2], бизнес-проектов малого и среднего бизнеса, оценки эффективности проектов производственного, финансового, коммерческого и управленческого содержания.

Заключение

АИС «ЛЭД» является удобным инструментом поддержки принятия решений при анализе проектов планирования и прогнозирования экономической деятельности различных инвестиционно-производственных структур в форме оптимизационных задач линейной экономической динамики с дисконтированием коэффициентов в критериях, а его графоаналитический инструментарий позволяет исследователю проводить многопараметрический анализ получаемых результатов, интерпретировать и оценивать их содержательную адекватность, на основании чего принимать эффективные инвестиционные, производственные и финансовые решения, зная при этом, что они соответствуют максимально возможным значениям критериев эффективности развития предприятия.

Библиографическая ссылка