Постоянный рост пользователей WiFi-гаджетов приводит к ситуации, когда существующие стандарты обеспечения беспроводной системы связи не позволяют в полной мере удовлетворить возрастающие потребности. Это приводит к необходимости введения нового протокола для мобильной связи, в частности 5G. В настоящее время разработан проект стандарта IMT-2020, согласно которому перспективные сети мобильной связи 5G должны обладать характеристиками, которые превосходят стандарты 4G. Переход к новым технологиям позволит обеспечивать скорость передачи информации не ниже 10 Гбит/c. При этом величина сетевой задержки на должна превысить 1 мс. Выдвигаемые в проекте стандарта IMT-2020 требования к перспективному протоколу 5G позволят обеспечить эффективное обслуживание до миллиона устройств на один квадратный километр [1–3].
В основе принципов построения беспроводных сетей 5G лежат две технологии. Первая представляет широкополосную передачу с использованием гребенчатой фильтрации FBMC (Filter Bank MultiCarrier) [4]. В основе второй лежит использование универсальной фильтрации UFMC (Universal Filtered MultiCarrier) [5]. Благодаря применению такого подхода обеспечивается повышение показателей качества обслуживания, которые были обеспечены в системах беспроводной связи LTE/LTE-Advanced и стандарте IEEE 802.11a/g/n/ac. В частности, использование фильтров позволяет отказаться от циклического префикса, улучшив спектральную эффективность сигнала OFDM. Однако при этом возрастают вычислительные затраты на выполнение процедур цифровой фильтрации, что приводит к увеличению сетевой задержки. Поэтому разработка быстрого алгоритма выполнения теоретико-числовых преобразований сигналов для систем OFDM, поддерживающих стандарт 5G, является актуальной задачей.
При разработке проекта развертывания сетей 5G планируется, что достижение поставленной цели на повышение скорости передачи информации возможно за счет повышения архитектуры сетей 4G. Для этого необходимо обеспечить применение перспективных технологий цифровой фильтрации FBMC и UFMC [4, 5]. Однако дополнительная цифровая обработка сигнала, направленная на более качественное подавление боковых лепестков поднесущих, требует достаточно большого объема вычислений, что снижает скорость передачи информации. Проведенные исследования показали, что применение метода UFMC позволяет обеспечить более качественную фильтрацию поднесущей по сравнению с гребенчатой фильтрацией FBMC. Однако использование данного метода требует больших вычислительных затрат, что негативно влияет на скорость передачи информации и на сетевые задержки. Поэтому целью статьи является снижение величины сетевых задержек при применении технологии фильтрации UFMC-сигналов за счет использования быстрого алгоритма выполнения теоретико-числового преобразования (ТЧП).
Материалы и методы исследования
Стремление повысить эффективность мобильных сетей 5G привело к активизации работ по модификации технологии OFDM. Для повышения спектральной эффективности сигнала с частотным ортогональным мультиплексированием предлагается использование дополнительной цифровой обработки сигналов. В настоящее время существуют два основных подхода по реализации в технологии OFDM методов цифровой фильтрации. В работах [2–5] показано, что основу первого подхода составляют методы широкополосной передачи на основе FBMC-фильтрации. В основе второго подхода предлагается использовать универсальную UFMC-фильтрацию (Filter Bank MultiCarrier) обеспечения сигнала.
Первая представляет методы широкополосной передачи с использованием гребенчатой фильтрации FBMC (Filter Bank MultiCarrier). В основе второй лежит использование универсальной фильтрации UFMC (Universal Filtered MultiCarrier). Благодаря применению такого подхода обеспечивается повышение показателей качества обслуживания, которые были обеспечены в системах беспроводной связи LTE/LTE-Advanced и стандарте IEEE 802.11a/g/n/ac. В частности, использование фильтров позволяет отказаться от циклического префикса, улучшив спектральную эффективность сигнала OFDM [1, 2].
На рис. 1 приведена функциональная схема передающего устройства, использующего технологию UFMC-фильтрации без учета блоков, осуществляющих цифро-аналоговое преобразование и переноса частоты для передачи по каналу связи.
При реализации технологии UFMC необходимо последовательный поток, состоящий из N двоичных символов, разбить на В параллельных блоков. Каждый такой блок поступает на входы QAM-модуляторов. Затем последовательный поток символов 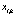 , где
, где 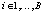 ,
, 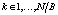 , с выходов QAM-модуляторов подаются на входы преобразователей последовательных потоков отсчетов в параллельные (S/P), а затем на входы блоков 2N-pt IFFT, реализующих 2N – точечное обратное быстрое преобразование Фурье (ОБПФ). Размер ОБПФ определяется необходимостью получения вещественных временных составляющих. Для этого в каждый блок добавляются комплексно-сопряженные QAM-символы. Такой подход позволяет получить частотный диапазон, включающий в себя В последовательно расположенных поддиапазонов, в которых содержится N/B информационных поднесущих, что показано на рис. 1.
, с выходов QAM-модуляторов подаются на входы преобразователей последовательных потоков отсчетов в параллельные (S/P), а затем на входы блоков 2N-pt IFFT, реализующих 2N – точечное обратное быстрое преобразование Фурье (ОБПФ). Размер ОБПФ определяется необходимостью получения вещественных временных составляющих. Для этого в каждый блок добавляются комплексно-сопряженные QAM-символы. Такой подход позволяет получить частотный диапазон, включающий в себя В последовательно расположенных поддиапазонов, в которых содержится N/B информационных поднесущих, что показано на рис. 1.
Полученные вещественные временные составляющие Xi,k, где 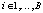 ,
, 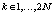 , с выходов блоков 2N-pt IFFT, реализующих 2N–точечного ОБПФ, с помощью преобразователей P/S преобразуются в последовательный поток. Затем временные составляющие сигнала поступают на входы КИХ-фильтров, которые на рис. 1 обозначены как Band Filter Fi, length L. Данные цифровые фильтры имеют конечную импульсную характеристику, которая определяется информационными поднесущими соответствующих поддиапазонов.
, с выходов блоков 2N-pt IFFT, реализующих 2N–точечного ОБПФ, с помощью преобразователей P/S преобразуются в последовательный поток. Затем временные составляющие сигнала поступают на входы КИХ-фильтров, которые на рис. 1 обозначены как Band Filter Fi, length L. Данные цифровые фильтры имеют конечную импульсную характеристику, которая определяется информационными поднесущими соответствующих поддиапазонов.
Известно, что длина КИХ-фильтра L оказывает первостепенное влияние на спектральную характеристики систем связи, использующих UFMC-фильтрацию. Для уменьшения величины спектральных составляющих, находящихся за пределами полосы пропускания, необходимо увеличивать порядок фильтра. Следует отметить, что это также способствует повышению устойчивости КИХ-фильтра к искажениям в многолучевом канале и ошибкам синхронизации [6]. Поэтому в системах 5G, использующих UFMC-фильтрацию, предлагают выбирать порядок фильтра равный 7 % от величины блока ОБПФ.
Однако, улучшая спектральные составляющие сигнала 5G, дополнительная UFMC-фильтрация оказывает негативное влияние на временные показатели обработки сигналов.
Дополнительная фильтрация приводит к увеличению вычислений, требуемых для формирования символов. Так, для получения вещественных временных отсчетов сигнала OFDM требуется выполнить 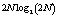 операций комплексного умножения, а также
операций комплексного умножения, а также 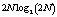 операций комплексного сложения. Тогда временные затраты для формирования символа UFMC будут в В раз больше чем затраты при реализации ОБПФ. Это связано с тем, что 2N временных отсчета, снятых после выполнения ОБПФ, подвергаются цифровой фильтрации, в основе которой лежит линейная свертка
операций комплексного сложения. Тогда временные затраты для формирования символа UFMC будут в В раз больше чем затраты при реализации ОБПФ. Это связано с тем, что 2N временных отсчета, снятых после выполнения ОБПФ, подвергаются цифровой фильтрации, в основе которой лежит линейная свертка
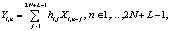 (1)
(1)
где Yi,n – отклик цифрового фильтра; Xi,k – входная последовательность вещественных отсчетов; hi,l – весовые коэффициенты фильтра; 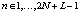 ;
; 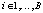 ;
; 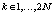 ; L – порядок КИХ-фильтра.
; L – порядок КИХ-фильтра.
В результате использования такого фильтра для выполнения цифровой фильтрации, потребуется 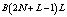 операций умножений [6]. Очевидно, что увеличение порядка фильтра L будет приводить к значительным временным задержкам, которые связаны с необходимостью получения отклика.
операций умножений [6]. Очевидно, что увеличение порядка фильтра L будет приводить к значительным временным задержкам, которые связаны с необходимостью получения отклика.
Для уменьшения величины сетевой задержки при использовании UFMC-фильтрации предлагается использовать циклическую свертку входной последовательности Xi,k и коэффициентов КИХ-фильтра hi,l. Сначала вещественные значения отсчетов Xi,k, где 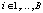 ,
, 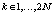 , преобразуем в целочисленный формат вида
, преобразуем в целочисленный формат вида 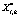 . Аналогичным образом поступим с коэффициентами КИХ-фильтра hi,l. В результате получаем
. Аналогичным образом поступим с коэффициентами КИХ-фильтра hi,l. В результате получаем 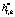 , где
, где 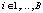 ,
, 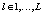 . Так как значение N выбирается из условия, что это степень двойки, то добавим к входной последовательности 2N нулей. А к коэффициентам КИХ-фильтра – 4N – L нулей. Это позволяет получить две последовательности, которые имеют длину, равную 4N, к которой можно применить циклическую свертку.
. Так как значение N выбирается из условия, что это степень двойки, то добавим к входной последовательности 2N нулей. А к коэффициентам КИХ-фильтра – 4N – L нулей. Это позволяет получить две последовательности, которые имеют длину, равную 4N, к которой можно применить циклическую свертку.
Для повышения скорости выполнения цифровой фильтрации на основе теоретико-числового преобразования можно воспользоваться свойством циклической свертки. Для этого необходимо найти теоретико-числовые образы обрабатываемых последовательностей 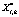 и
и 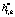 .
.
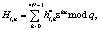 (2)
(2)
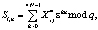 (3)
(3)
где 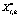 и
и 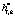 – обрабатываемые последовательности, Si,n и Hi,k – результаты преобразования, ε – ядро теоретико-числового преобразования; q – простое число;
– обрабатываемые последовательности, Si,n и Hi,k – результаты преобразования, ε – ядро теоретико-числового преобразования; q – простое число; 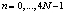 .
.
Затем найти произведение результатов преобразования
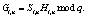 (4)
(4)
После этого к полученному результату применяют обратное теоретико-числовое преобразование. Тогда имеем
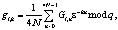 (5)
(5)
где N и q – взаимно простые натуральные числа, ε удовлетворяет условиям 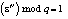 .
.
Очевидно, что выигрыш в производительности выполнения выражения (2)–(5) возможен, если использовать быстрый алгоритм вычисления ТЧП. В работах [7, 8] представлен алгоритм быстрого выполнения ТЧП, который по своей структуре аналогичен быстрому преобразованию Фурье (БПФ). При длине входной последовательности равной M теоретико-числового преобразования сигнала может быть реализовано за 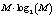 операций умножений.
операций умножений.
Результаты исследования и их обсуждение
Рассмотрим реализацию разработка быстрого алгоритма выполнения теоретико-числовых преобразований сигналов для систем 5G, использующих технологию OFDM. Для проведения сравнительного анализа была разработана имитационная модель в среде Matlab2017. В качестве КИХ UFMC-фильтра выбран КИХ-фильтр Дольфа – Чебышева. Размер окна, определяемый импульсной характеристикой цифрового фильтра, составляет 74 отсчета. Ослабление UFMC-фильтра за пределами полосы пропускания составляет 60 дБ. Выбранный размер теоретико-числового преобразования – 2048 отсчетов. Модуль, используемый при реализации ТЧП, равен q = 974849.
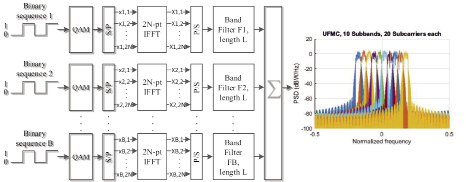
Рис. 1. Функциональная схема передающего устройства, реализующего UFMC-фильтрацию
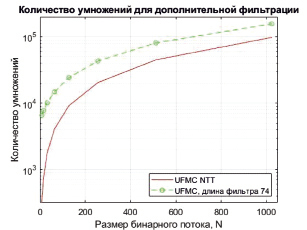
Рис. 2. Количество умножений при выполнении фильтрации в технологиях UFMC и UFMC NTT
Очевидно, что при выполнении быстрого алгоритма ТЧП рассмотренной выше свертки понадобится выполнить 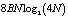 операций умножения по модулю q. При этом ТЧП-образы коэффициентов КИХ-фильтр Дольфа – Чебышева могут быть получены заранее. Поэтому для реализации предложенного быстрого алгоритма выполнения ТЧП необходимо выполнить выражения (3)–(5).
операций умножения по модулю q. При этом ТЧП-образы коэффициентов КИХ-фильтр Дольфа – Чебышева могут быть получены заранее. Поэтому для реализации предложенного быстрого алгоритма выполнения ТЧП необходимо выполнить выражения (3)–(5).
Сравнительный анализ разработанного быстрого алгоритма выполнения ТЧП будем осуществлять с классическим подходом, вычисления отклика цифрового UFMC-фильтра. На рис. 2 показана зависимость количества умножений при выполнении фильтрации в технологиях UFMC и UFMC NTT от размера N бинарного потока передаваемых данных в одном подканале сигнала OFDM. Так как операция умножения требует наибольших временных затрат на свое выполнение по сравнению с другими арифметическими операциями, то сокращение количества данной операции буде положительно сказываться на времени вычисления ТЧП.
Анализ рис. 2 показывает, что использование разработанного быстрого алгоритма выполнения ТЧП позволяет уменьшить количество операций умножения по сравнению с классическими методами выполнения цифровой фильтрации. Так при длине входной последовательности N = 512 отсчетов количество целочисленных умножений при выполнении UFMC-фильтрации с использованием разработанного алгоритма составит 36864 операций. При этом для выполнения UFMC-фильтрации потребуется 81178 операций умножения. Значит, использование разработанного быстрого алгоритма ТЧП позволяет сократить количество операций умножения в 2,2 раза по сравнению с классической реализацией UFMC-фильтрации. Таким образом, очевидно, что реализация быстрого алгоритма ТЧП позволит сократить сетевую задержку при применении технологии фильтрации UFMC-сигналов.
Заключение
В работе показано применение разработанного быстрого алгоритма выполнения теоретико-числового преобразования сигналов в беспроводных системах 5G. Использование разработанного алгоритма позволило уменьшить количество операций умножения при выполнении UFMC-фильтрации. Так при обработке дискретной входной последовательности из N = 512 отсчетов количество целочисленных умножений при выполнении UFMC-фильтрации с использованием разработанного алгоритма составит 36864 операции. При этом для выполнения UFMC-фильтрации потребуется 81178 операций умножения, что в 2,2 раза больше по сравнению с разработанным алгоритмом. А так как операция умножения является наиболее затратной по времени, то очевидно, что использование разработанного быстрого алгоритма ТЧП позволяет сократить сетевую задержку при применении технологии фильтрации UFMC-сигналов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-37-00009.
Библиографическая ссылка
Калмыков М.И., Юрданов Д.В., Степанова Е.П., Калмыков И.А., Топоркова Е.В. РАЗРАБОТКА БЫСТРОГО АЛГОРИТМА ВЫПОЛНЕНИЯ ТЕОРЕТИКО-ЧИСЛОВЫХ ПРЕОБРАЗОВАНИЙ СИГНАЛОВ ДЛЯ СИСТЕМ OFDM // Современные наукоемкие технологии. 2019. № 10-2. С. 257-261;URL: https://top-technologies.ru/ru/article/view?id=37733 (дата обращения: 13.03.2026).



