В данной статье сравнивается определение приоритета принятия решения посредством метода анализа иерархий и предложенного авторами способа выбора рационального решения. Сам способ по своей сути основывается на методе анализа иерархий и призван стать математическим инструментом системного подхода к сложным проблемам принятия решений [1]. Отличается данный способ от классического применения метода анализа иерархий: применением прямых отношений величин (показателей, характеристик) альтернатив при построении матриц относительных оценок, а также транспонированием матриц оценок альтернативных вариантов.
Цель исследования: повышение объективности принятия решения в случае использования нескольких разнородных критериев, применяя учет коэффициента согласованности оценок экспертов. Для сравнения точности принятия решения будет решена задача выбора сорта яблок. При решении указанной задачи необходимо выбрать сорт яблок, обладающий минимальной среднерыночной стоимостью саженца, максимальным средним временем хранения и средней массой плода, а также хорошими вкусовыми качествами. Сравниваемые образцы яблок: «Айдаред», «Шафран», «Северный Синап» – обладают следующими характеристиками, представленными в табл. 1.
Для удобства расчетов и их отображения введем следующие обозначения: «Айдаред» – Я1, «Шафран» – Я2, «Северный синап» – Я3, «Среднее время хранения» – tхр, «Средняя масса плода» – mср, «Среднерыночная стоимость» – Сср; «Вкусовые качества» – Вк.
Материалы и методы исследования
Так как при классическом применении метода анализа иерархий строятся матрицы оценок альтернативных вариантов по соответствующим критериям на основе шкалы относительной важности, разработанной Т. Саати, то необходимо задействовать экспертов [2]. Исходя из этого, сформируем группу экспертов, проверим их на согласованность и построим матрицы оценок альтернативных вариантов по критериям: среднее время хранения, средняя масса плода, среднерыночная стоимость – и по критерию вкусовые качества. В табл. 2 приведен расчет матрицы оценок альтернатив по критерию среднее время хранения для эксперта № 1, аналогичным образом произведен расчет для других критериев и остальных девяти экспертов.
Проверим суждения экспертов на согласованность и рассчитаем средние значения нормированных векторов оценок экспертов.
Согласованность экспертов определим по коэффициенту конкордации (W):
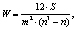 (1)
(1)
где m – число экспертов, n – количество суждений по взаимной значимости критериев или по значимости альтернативы по соответствующему критерию.
Далее построим матрицы оценок суждений экспертов по соответствующим критериям. В табл. 3 приведен расчет матрицы оценок суждений экспертов по критерию среднее время хранения эксперту № 1, таким же образом произведен расчет для других критериев и экспертов.
Степень согласованности оценок суждений экспертов по критериям [3]: среднее время хранения, средняя масса плода, среднерыночная стоимость и вкусовые качества составляет
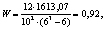 (2)
(2)
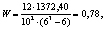 (3)
(3)
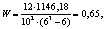 (4)
(4)
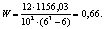 (5)
(5)
Таблица 1
Количественные и качественные характеристики рассматриваемых сортов яблок
|
Наименование сорта |
Среднее время хранения, мес. |
Средняя масса плода, гр. |
Среднерыночная стоимость, руб. |
Вкусовые качества |
|
Айдаред |
6 |
200 |
900 |
кисло-сладкий |
|
Шафран |
3 |
110 |
800 |
сладкий |
|
Северный синап |
7 |
120 |
800 |
кисло-сладкий |
Таблица 2
Матрица оценок альтернативных вариантов по критерию среднее время хранения
|
Эксперт № 1 |
Я1 |
Я2 |
Я3 |
Норм. вектор |
|
Я1 |
1 |
4,00 |
0,50 |
1,32 |
|
Я2 |
0,25 |
1 |
0,13 |
0,33 |
|
Я3 |
2,00 |
8,00 |
1 |
2,64 |
Таблица 3
Матрица оценок суждений экспертов по критерию среднее время хранения
|
Эксперты |
n |
Σ |
|||||
|
Я1/Я2 |
Я1/Я3 |
Я2/Я1 |
Я2/Я3 |
Я3/Я1 |
Я3/Я2 |
||
|
Эксперт № 1 |
4,00 |
0,50 |
0,25 |
0,13 |
2,00 |
8,00 |
|
|
Сумма рангов по каждому суждению |
30,00 |
7,00 |
3,70 |
2,62 |
16,00 |
48,00 |
107,32 |
|
Отклонение от средней суммы рангов |
12,82 |
–10,18 |
–13,48 |
–14,56 |
–1,18 |
30,82 |
|
|
Квадраты отклонений сумм рангов |
164,40 |
103,59 |
181,66 |
212,03 |
1,39 |
950,00 |
1613,07 |
Таблица 4
Нормированный вектор средних значений оценок суждений экспертов по критерию среднее время хранения
|
Наименование сорта |
Нормированные вектора экспертов |
Норм. вект. сред. |
|||||||||
|
Экс. № 1 |
Экс. № 2 |
Экс. № 3 |
Экс. № 4 |
Экс. № 5 |
Экс. № 6 |
Экс. № 7 |
Экс. № 8 |
Экс. № 9 |
Экс. № 10 |
||
|
Я1 |
1,32 |
1,20 |
1,27 |
1,13 |
1,08 |
1,29 |
0,91 |
1,16 |
1,12 |
0,87 |
1,13 |
|
Я2 |
0,33 |
0,60 |
0,42 |
0,38 |
0,36 |
0,26 |
0,46 |
0,58 |
0,28 |
0,43 |
0,41 |
|
Я3 |
2,64 |
1,20 |
1,27 |
2,26 |
2,15 |
1,29 |
1,82 |
1,16 |
2,24 |
1,73 |
1,78 |
Таблица 5
Матрица оценок суждений экспертов о взаимной значимости критериев
|
Эксперты |
n |
∑ |
|||||||||||
|
tхр/mср |
tхр/Сср |
tхр/ Вк |
mср/tхр |
mср/Сср |
mср/Вк |
Сср/tхр |
Сср/mср |
Сср/Вк |
Вк/ tхр |
Вк/ mср |
Вк/ Сср |
||
|
Эксперт № 1 |
9,00 |
8,00 |
3,00 |
0,11 |
0,89 |
0,33 |
0,13 |
1,13 |
0,38 |
0,33 |
3,00 |
2,67 |
|
|
Сумма рангов по каждому суждению |
72,00 |
58,24 |
4,18 |
1,48 |
55,89 |
1,54 |
18,12 |
2,80 |
1,49 |
71,35 |
72,00 |
76,69 |
436 |
|
Отклонение от средней суммы рангов |
35,68 |
21,92 |
–32,14 |
–34,84 |
19,57 |
–34,77 |
–18,19 |
–33,51 |
–34,83 |
35,04 |
35,69 |
40,38 |
|
|
Квадраты отклонений сумм рангов |
1273 |
481 |
1033 |
1214 |
383 |
1209 |
331 |
1123 |
1213 |
1228 |
1274 |
1630 |
12391 |
Таблица 6
Нормированный вектор средних значений оценок суждений экспертов о значимости соответствующего критерия
|
Критерии |
Нормированные вектора экспертов |
Норм. вект. сред. |
|||||||||
|
Экс. № 1 |
Экс. № 2 |
Экс. № 3 |
Экс. № 4 |
Экс. № 5 |
Экс. № 6 |
Экс. № 7 |
Экс. № 8 |
Экс. № 9 |
Экс. № 10 |
||
|
tхр |
2,55 |
0,84 |
1,18 |
1,32 |
1,14 |
1,12 |
1,35 |
0,67 |
0,88 |
0,97 |
1,20 |
|
mср |
0,28 |
0,46 |
0,42 |
0,42 |
0,40 |
0,31 |
0,48 |
0,80 |
0,87 |
0,28 |
0,47 |
|
Сср |
0,32 |
0,16 |
0,15 |
0,18 |
0,14 |
0,19 |
0,17 |
0,90 |
0,86 |
0,16 |
0,32 |
|
Вк |
0,85 |
3,35 |
3,33 |
3,48 |
3,40 |
3,17 |
2,76 |
2,92 |
2,97 |
3,43 |
2,97 |
Результаты расчета нормированного вектора средних значений оценок суждений экспертов по критерию среднее время хранения представлены в табл. 4, аналогичным образом произведен расчет и для других критериев.
Кроме того, необходимо сформировать матрицу оценок суждений экспертов о взаимной значимости критериев (табл. 5) и на ее основе рассчитать нормированный вектор средних значений оценок суждений эксперта № 1 о значимости соответствующего критерия (табл. 6), а также аналогично получить данные для других экспертов, затем согласно предыдущим выкладкам определить коэффициент конкордации (формула 6) [4].
Далее необходимо из нормированных векторов матриц оценок альтернативных вариантов по соответствующему критерию (табл. 4) сформировать матрицу (табл. 7) размерностью m×n, где m – количество сравниваемых альтернатив, а n – количество критериев по которым проводится сравнение [5].
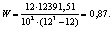 (6)
(6)
Таблица 7
Матрица нормированных векторов оценок суждений экспертов по соответствующему критерию
|
Наименование показателя |
n |
||||
|
tхр |
mср |
Сср |
Вк |
||
|
m |
Я1 |
1,13 |
1,17 |
0,77 |
1,54 |
|
Я2 |
0,41 |
0,42 |
3,13 |
0,39 |
|
|
Я3 |
1,78 |
1,68 |
1,08 |
1,13 |
|
После чего умножить сформированную матрицу, элементы которой представлены в табл. 7, на нормированный вектор оценок суждений экспертов о значимости соответствующего критерия (табл. 6). Произведение матрицы на нормированный вектор представлено формулой
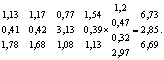 (7)
(7)
В результате получен глобальный вектор приоритета, который показывает, что, исходя из оценок экспертов, сорт яблок «Северный синап» наиболее приемлем с точки зрения времени хранения, массы плода, среднерыночной стоимости и вкусовых качеств.
Теперь рассмотрим определение приоритета принятия решения при выборе сорта яблок, если применить предложенный авторами способ выбора рационального решения. В данном способе предлагается следующий алгоритм обработки экспертных оценок: взамен шкалы относительной важности перейти к прямым отношениям одноименных величин в тех случаях, когда сравниваемые альтернативы обладают четко выраженными количественными характеристиками. Например, если сравниваемые объекты обладают массой, тогда при их парном сравнении необходимо массу объекта, находящегося в строке, отнести к массе объекта, находящегося в столбце, и таким образом заполнить всю матрицу парных сравнений, т.е. заполнить оценками в виде прямых отношений сравниваемых альтернатив по соответствующему критерию [6]. Исходя из этого, получаем матрицу оценок альтернативных вариантов по критерию среднее время хранения (табл. 8) и аналогичным образом производим расчет для других критериев.
Таблица 8
Матрица оценок альтернативных вариантов по критерию среднее время хранения
|
tхр |
Я1 |
Я2 |
Я3 |
Норм. вектор |
|
Я1 |
1 |
2,00 |
0,86 |
1,13 |
|
Я2 |
0,50 |
1 |
0,43 |
0,56 |
|
Я3 |
1,17 |
2,33 |
1 |
1,31 |
Так как по критерию вкусовые качества сравниваемые альтернативы не обладают количественными характеристиками и оценены экспертами в предыдущих выкладках, то значения матриц оценок суждений экспертов о взаимной значимости критериев, матриц суждений экспертов по критерию вкусовые качества, а также соответствующие им коэффициенты конкордации остаются неизменными.
После того как заполнены матрицы оценок альтернативных вариантов по критериям (среднее время хранения, средняя масса плода, среднерыночная стоимость, вкусовые качества) и проверена согласованность экспертов, необходимо провести транспонирование тех матриц оценок альтернативных вариантов по критериям, которые должны выйти в глобальный вектор приоритетов с минимальными характеристиками [7]. Другими словами, это делается для того, чтобы в глобальном векторе приоритетов, например, по критерию «среднерыночная стоимость», на лидирующие позиции выходили наиболее дешевые сорта яблок, а не самые дорогие.
Транспонирование матрицы оценок альтернативных вариантов по критерию среднерыночная стоимость представлено в табл. 9.
Далее аналогично вышеуказанным выкладкам формируется матрица нормированных векторов оценок суждений экспертов и прямых отношений их количественных характеристик по соответствующему критерию (табл. 10). После чего рассчитывается глобальный вектор приоритета (формула 8).
Таблица 9
Транспонированная матрица оценок альтернативных вариантов по критерию среднерыночная стоимость
|
Сср |
Я1 |
Я2 |
Я3 |
Норм. вектор |
|
Я1 |
1 |
0,89 |
0,89 |
0,92 |
|
Я2 |
1,13 |
1 |
1,00 |
1,04 |
|
Я3 |
1,13 |
1,00 |
1 |
1,04 |
Таблица 10
Матрица нормированных векторов оценок (средних значений оценок) суждений экспертов по соответствующему критерию
|
Наименование показателя |
n |
||||
|
tхр |
mср |
Сср |
Вк |
||
|
m |
Я1 |
1,13 |
1,4 |
0,92 |
1,49 |
|
Я2 |
0,56 |
0,77 |
1,04 |
0,40 |
|
|
Я3 |
1,31 |
0,84 |
1,04 |
1,13 |
|
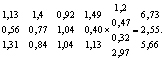 (8)
(8)
Исходя из имеющихся данных по количественным характеристикам рассматриваемых сортов яблок, а также с учетом оценок экспертов сорт яблок «Айдаред» наиболее приемлем. Однако это противоречит результатам, полученным в первой части статьи, при классическом применении метода анализа иерархий. В свою очередь, прямые отношения реально существующих характеристик нельзя считать ошибочными в силу их физического естества. В результате остается единственно верным искать ошибку в оценках данных экспертами.
Результаты исследования и их обсуждение
Сама теория экспертных оценок оговаривает этот случай так: «чем выше степень согласованности экспертной группы, тем ниже вероятность ошибки» [8]. Однако в рассматриваемом примере и так высокая степень согласованности, в среднем по четырем критериям порядка 0,75. На данном примере наглядно показано повышение объективности принятия решения (рисунок). При сравнении данных, полученных методом анализа иерархий на основе экспертных оценок с аналогичными значениями, полученными, на основе того же метода, но с применением прямых отношений показателей (характеристик) альтернатив и транспонирования матриц относительных оценок альтернативных вариантов.
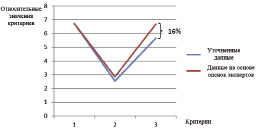
Сравнение полученных результатов при выборе рационального решения
Таким образом, предложенный способ призван обеспечить корректность сравнения альтернатив и степень обоснованности предпочтительного варианта решения. Разработанные процедуры удобны для алгоритмизации и программирования, что будет способствовать автоматизации процесса сравнительного анализа и экспертизы альтернатив.
Выводы
Полученные результаты позволяют считать, что предлагаемый авторами способ выбора рационального решения позволяет повысить объективность принятия решения по отдельным критериям до 16 % исходя их конкретно рассматриваемого случая. Развитие и внедрение данного способа позволит расширить математический инструмент системного подхода к сложным проблемам принятия решения.
Библиографическая ссылка
Золотухин С.И., Дьяков Д.Е., Зибров Р.С., Котляров П.С. ТОЧНОСТЬ РАСЧЕТОВ ПРИ ПРИМЕНЕНИИ СПОСОБА ВЫБОРА РАЦИОНАЛЬНОГО РЕШЕНИЯ // Современные наукоемкие технологии. 2019. № 10-2. С. 252-256;URL: https://top-technologies.ru/ru/article/view?id=37732 (дата обращения: 06.02.2026).



