Задачи об одноосном растяжении плоских и цилиндрических образцов в условиях плоской и осесимметричной деформации рассматривались в работах [1–3]. Алгоритм решения рассматриваемой задачи в целом соответствует указанным работам.
Еще одним решением задачи о растяжении полосы в условиях плоского напряженного состояния будет решение аналогично решению Е. Оната и В. Прагера при плоской деформации.
Цель работы: исследование и анализ зависимостей полей скоростей деформаций от относительных удлинений, возникающих при деформировании образца. Также целью данной работы является определение наиболее предпочтительных моделей поведения образца при различных полях скоростей перемещения и сравнительный анализ зависимостей деформирования образца как при плоской деформации, так и при плоском напряженном состоянии.
Материалы и методы исследования
Рассмотрим растяжение полосы с разрывным полем скоростей перемещений. Пластическая деформация в данном случае локализуется вдоль линий разрыва скоростей перемещений. Особенностью данной задачи являются разрывность поля скоростей перемещений и скачкообразное увеличение деформаций при пересечении частицей линий разрыва скоростей и локализация деформаций в заштрихованной области (рис. 1).
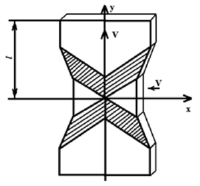
Рис. 1. Растяжение полосы при неоднородном поле скоростей перемещений
Пусть L – линия разрыва скоростей перемещений Vi, которая распространяется с нормальной скоростью Gi.
Деформация частицы в условиях плоского напряженного состояния при пересечении линии разрыва скоростей перемещений [4] (L) будет иметь вид (рис. 2), и нормальная скорость линии определяется по формуле: Gi = –Gνi.
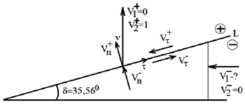
Рис. 2. Скорости деформаций
Движение среды будет описываться в форме Эйлера.
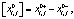
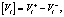(1)
«+» и «–» определенная сторона линии разрыва.
Будем считать, что ниже линии разрыва L [5] материал недеформирован:
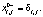(2)
Для разрывов производных имеют место геометрические и кинематические условия совместности:
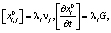(3)
νj – единичный вектор нормали, τj – единичный вектор касательной с координатами ν(0,1), τ(1,0).
Вдоль траектории материальной частицы лагранжевы координаты постоянны:
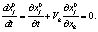(4)
Получаем
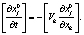(5)
Из соотношений (2) и (3) получаем
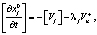(6)
где [Vj] – вектор разрыва скорости перемещения, который определяется в виде
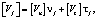
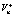– нормальная скорость движения частины на линии разрыва.
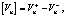
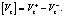
Из уравнений (1)–(4) получаем
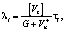
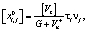(7)
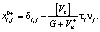(8)
Значение диссипации энергии для разрывного поля скоростей [6] перемещений при плоском напряженном состоянии имеет вид
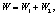
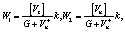
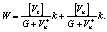
Объемная плотность диссипации энергии, получаемой материальной частицей при пересещении поверхности разрыва скоростей, имеет вид
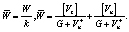(9)
Разрыв тензора градиентов перемещения имеет вид
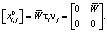(10)
Из (10) получаем компоненты тензора Альманси в виде
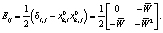(11)
Главные значения тензора Альманси согласно (11) имеют вид
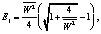
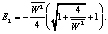
Из условия несжимаемости:
Получаем
E3 = 0. (12)
Определим значение объемной плотности энергии диссипации. Используя рис. 2, имеем
(13)
Необходимо найти значение скорости перемещений V1.
Для соотношения объемов при переходе через линию разрыва выполняются соотношения
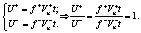(14)
Используя (14), получаем
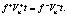(15)
Из (13) и (15) имеем
;
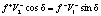пр условии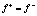 
имеем: 
;
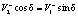так как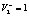 
, то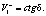 
Согласно (1) получаем
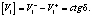(16)
Разрыв скорости перемещений из (12)–(15) в нормальном направлении имеет вид
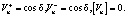(17)
Из (17) следует, что нормальная составляющая скорости перемещений непрерывна и скачок происходит только в касательном напралении. Из рис. 2 (совместно с (16) имеем
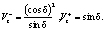(18)
Разрыв касательной состовляющей согласно (18) имеет вид
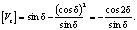(19)
Из соотношений (9), (12), (17), (19):
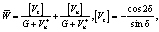
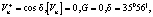(20)
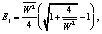
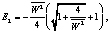E3 = 0.
Используя формулы (20), определим значения величин:
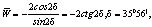
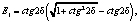(21)
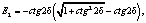
E3 = 0.
Результаты исследования и их обсуждение
Полученные зависимости (20) и (21) являются решением задачи о растяжении полосы с разрывным полем скоростей перемещений и позволяют найти тензор конечных деформаций Альманси (11).
Приведем сравнительный анализ решений, полученных для задачи растяжения полосы с непрерывным полем скоростей перемещений и задачи с разрывным полем скоростей перемещений. На рис. 3 представлены зависимости первого инварианта тензора деформации Альманси (E1) для решений с непрерывным и разрывным полем скоростей перемещений.
На рис. 4 изображены зависимости объемной плотности диссипации (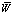
) энергии для различных полей скоростей [7] перемещений (непрерывного и разрывного поля скоростей перемещений).
На рис. 5 показаны графики зависимостей усилия (P), необходимого для растяжения полосы, от относительного удлинения образца (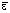
) для решений с непрерывным полем скоростей перемещений и разрывным полем скоростей перемещений.
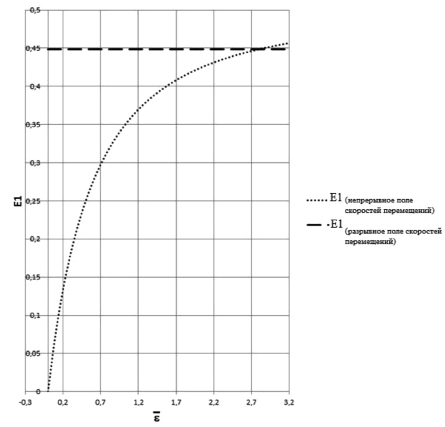
Рис. 3. Первое главное значение тензора деформации Альманси
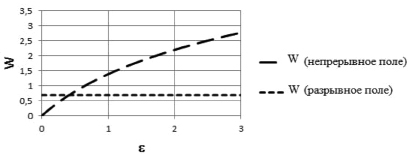
Рис. 4. Диссипация энергии
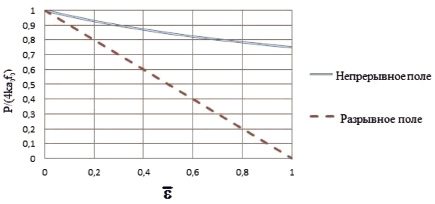
Рис. 5. Усилие, необходимое для растяжения образца
Заключение
Анализ полученных зависимостей показывает, что на начальном этапе деформирования решение с непрерывным полем скоростей перемещений при плоском напряженном состоянии приводит к меньшим деформациям частиц материала и к большим усилиям, необходимым для деформирования образца. Следовательно, модель с непрерывным полем скоростей перемещений более предпочтительна для реальных материалов (алюминиевые сплавы (7475, 1163, 1161, 2524 и т.д.), алюминиево-литиевые сплавы), причем анализ зависимостей, в отличие от плоской деформации образца, производится с учетом геометрии (изменение толщины и ширины образца). Данные выводы позволяют на ранних этапах деформирования оценить поведение элементы конструкции и сделать выводы о его деформировании в различных частях конструкции.
Результаты, полученные в данной работе, позволят принять соответствующие меры для предотвращения нежелательного деформирования и последующего разрушения материала, что приводит к возможному разрушению элемента конструкции.
Библиографическая ссылка
Хромов А.И., Григорьев Я.Ю., Григорьева А.Л., Жарикова Е.П. ДЕФОРМИРОВАНИЕ ПЛОСКОГО ОБРАЗЦА ПРИ РАЗРЫВНОМ ПОЛЕ СКОРОСТЕЙ ПЕРЕМЕЩЕНИЙ В УСЛОВИЯХ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ // Современные наукоемкие технологии. – 2019. – № 10-1. – С. 73-77;URL: https://top-technologies.ru/ru/article/view?id=37700 (дата обращения: 23.11.2024).