Пешеходные переходы являются той частью улично-дорожной сети, которая оказывает значительное влияние на время передвижения как автотранспорта, так и пешеходов [1]. В силу высокой интенсивности движения использование нерегулируемых переходов становится нецелосообразным и небезопасным. Использование светофоров с жестким режимом регулирования там, где интенсивность пешеходных потоков крайне неравномерна в течение дня, приводит к излишним затратам времени. В таких случаях оптимизировать движение позволяют переходы, обустроенные вызывными устройствами для пешеходов типа Puffin, Pelican, Toucan.
С целью выбора оптимального режима функционирования вызывных устройств, а также прогнозирования времени в пути для автомобильного транспорта и пешеходов, необходимо иметь аналитический аппарат для оценки величины задержек транспортных и пешеходных потоков на переходах с вызывными устройствами. Причем по причине внедрения Интеллектальных транспортных систем актуальной задачей является разработка такой модели оценки, которая использовала бы мезоскопическую детализацию данных и позволяла бы получать результаты на текущий момент и прогнозировать их на ближайшее время.
Таким образом, целью исследования явялется разработка методов оценки задержек автотранспорта и пешеходов на переходах с вызывными устройствами.
Материалы и методы исследования
Ранее автором была разработана мезоскопическая модель TIMeR_Mod распределения транспортных потоков по улично-дорожной сети. При ее разработке принято, что интервалы по времени между автотранспортными потоками на каждой из полос для движения приняты подчиненными обобщенному закону Эрланга. При построении модели движения транспортных и пешеходных потоков будем оставаться в рамках предположений модели TIMeR_Mod.
В настоящее время моделированию пешеходных потоков уделяется достаточно много внимания в силу востребованности во многих отраслях. Например, при планировании публичных зданий и сооружений, остановок общественного транспорта, аэропортов и вокзалов, при проведении массовых общественных мероприятий необходимо моделировать поведение людей в тех или иных ситуациях, а также в случае паники. При этом в каждом случае требуется различная точность, особая важность тех или иных апсектов в поведении пешеходного потока. В настоящее время существуют микроскопические, мезоскопические и макроскопические модели пешеходного движения [2–4]. Микроскопичееские модели учитывают позицию, скорость и силы, действующие на каждого отдельного человека. Здесь можно выделить клеточную модель выгодной стоимости (Benefit Cost Cellular Model), модель клеточных автоматов (Cellular Automata Model), модель магнитных сил (Magnetic Force Model) и модель социальных сил (Social Force Model). В клеточной модели выгодной стоимости все пространство разбито на клетки, в каждой из которых может находиться или не находиться человек. В зависимости от того, занята клетка, свободна или граничит с занятой, ей присваивается стоимость. Передвижение пешехода отражается в модели как изменение стоимости клеток.
Модель магнитных сил описывает движение отдельного пешехода, который движется к своей цели и избегает столкновений, с помощью сил притяжения или отталкивания между ним и другими объектами и пешеходами.
В модели клеточных автоматов прогулка моделируется как передвижение по ячейкам сетки. Для описания движения составляется матрица, элементами которой являются вероятности для пешехода занять соседние ячейки.
Модель социальных сил считается лучшей среди микроскопических моделей и достаточно глубоко разработана. Согласно этой модели, пешеход – это объект, которого мотивируют социальные силы. Пешеход стремится достичь цели, причем наиболее комфортным для себя способом. Кроме того, каждый пешеход стремится сохранить комфортную для себя дистанцию от других пещшеходов и объектов. На основании этих положений составляются уравнения, описывающие поведение пешехода в потоке.
Модели, основанные на теории очередей (теории массового обслуживания), в разных источниках относят то к микроскопическим, то к мезоскопическим. Применяются они в том случае, когда поток движется в заданном направлении. Например, при моделировании процесса эвакуации людей из здания. При моделировании движения пешеходов по пешеходному переходу также применим этот тип моделей [5].
Результаты исследования и их обсуждение
1. Описание устройства. Рассмотрим пешеходный переход с вызывным устройством типа Pelpcan. Вызывное устройство расположено между перекрестками на значительном расстоянии. Неподалеку расположены «источники» пешеходного потока, например остановка общественного транспорта, учебное заведение, развлекательный центр и т.п. После нажатия кнопки вызывного устройства в течение времени tw пешеходы ожидают разрешающего сигнала (рисунок). Затем в течение фиксированного времени tgp I пешеходы пересекают дорогу. В течение tover горит запрещающий сигнал и для пешеходов, и для автотранспорта. В это время пешеходы заканчивают движение.
2. Описание пешеходного потока. Как было отмечено выше, модели, основанные на описании пешеходного потока как случайного с помощью случайных функций, используются в том случае, когда поток движется в заданном направлении. А следовательно, применимы при моделировании движения пешеходов по пешеходному переходу.
Пешеходный поток на подходах к пешеходному переходу можно рассматривать как поток «кластеров», движущихся в одном направлении. Кластеры образуются в результате выхода пассажиров из прибывшего к остановке общественного транспорта, после окончания сеанса в кинотеатре, после окончания занятий в учебном заведении и т.п. Кластер – это плотное скоплление людей, которым дотаточно одного нажатия кнопки вызывного устройства для перехода через дорогу.
Будем рассматривать кластер как отдельный объект. Распределение интервалов по времени между объектами (кластерами и отдельными «одиночными» пешеходами) примем подчиненным показательному закону c параметром λ 0 p.
3. Расчет задержек автотранспортного потока. В рамках математической модели TIMeR_Mod, поток прибывающих автомобилей является потоком Пальма, а интервалы по времени между транспортными средствами распределены по обобщенному закону Эрланга [6].
Найдем среднюю задержку автомобиля, случайно прибывающего к переходу. Под задержкой будем понимать время, проведенное в ожидании включения разрешающего сигнала светофора. Задержки, связанные со снижением скорости при приближении к переходу, не учитываются. Если транспортное средство прибывает к переходу в тот момент, когда пешеходов нет, оно проезжает без остановки. В противном случае ожидает включения разрешающего сигнала.

Схема включения запрещающего сигнала светофора для автотранспорта
3.1. Расчет средней задержки одного автотранспортного средства, прибывающего к пешеходному переходу.
Запрещающий сигнал для автотранспорта появляется в случайные промежутки времени согласно показательному закону с параметром λ 0 p. Длительность запрещающего сигнала фиксирована и равна 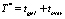 . Пусть X – случайная величина, время ожидания возможности продолжить движение. Так как параметр λ 0 p характеризует среднюю частоту появления события в единицу времени, то
. Пусть X – случайная величина, время ожидания возможности продолжить движение. Так как параметр λ 0 p характеризует среднюю частоту появления события в единицу времени, то
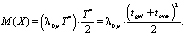 (1)
(1)
Формула (1) задает среднее значение задержки одного автотранспортного средства, прибывающего к пешеходному переходу в случае низкой интенсивности движения АТС по каждой из полос.
3.2. Расчет средней суммарной задержки автотранспортных средств, прибывающих к пешеходному переходу с вызывным устройством.
Вычислим предполагаемую суммарную задержку требований рассматриваемого потока за T* секунд – время, в течение которого запрещено движение АТС в рассматриваемом направлении по данной полосе. При этом будем считать, что в момент времени t = 0 очередь отсутствует.
При обобщенном распределении Эрланга интервал по времени между подряд идущими требованиями проходит k стадий 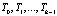 , причем длительности этих стадий имеют показательные распределения с параметрами
, причем длительности этих стадий имеют показательные распределения с параметрами 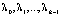 соответственно. Обозначим для удобства
соответственно. Обозначим для удобства 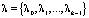 . Если все параметры λi различны, функция распределения обобщенного закона Эрланга имеет вид
. Если все параметры λi различны, функция распределения обобщенного закона Эрланга имеет вид
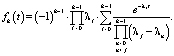 (2)
(2)
Математическое ожидание M(T) и дисперсия D(T) для обобщенного закона Эрланга равны соответственно
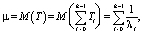
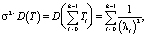 (3)
(3)
H(T) – функция восстановления для транспортного потока.
Разобьем интервал 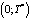 на n частей точками
на n частей точками 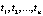 ;
; 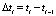 . Тогда суммарная задержка всех требований данного потока за один цикл T* приближенно равна
. Тогда суммарная задержка всех требований данного потока за один цикл T* приближенно равна
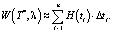 (4)
(4)
Перейдя к пределу при 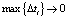 , получим:
, получим: 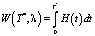 (треб.•с.)
(треб.•с.)
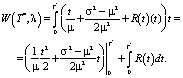 (5)
(5)
В работе [6] доказано, что функция R(T) может состоять только из следующих слагаемых:
1) 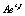 ;
;
2) 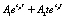 ;
;
3) 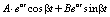 .
.
Соответствующие слагаемые в функции 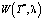 для каждого из перечисленных случаев также выведены в работе [6]:
для каждого из перечисленных случаев также выведены в работе [6]:
1) 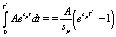 ; (6)
; (6)
2) 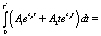
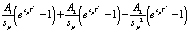 ; (7)
; (7)
3) 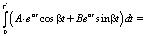
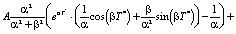
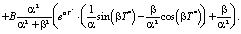 (8)
(8)
Средняя суммарная задержка (в часах) всех требований данного потока за единицу времени – один час, выражается следующим образом:
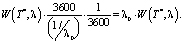 (9)
(9)
Если 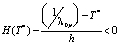 , то очередь в данном направлении ликвидируется за один цикл.
, то очередь в данном направлении ликвидируется за один цикл.
В таком случае можно уточнить формулу (1) для более высоких интенсивностей транспортных потоков:
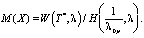 (10)
(10)
В случае высокой интенсивности пешеходного или транспортного потока возможно скопление очереди у перехода, что характеризуется выполнением следующего неравенства:
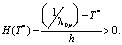 (11)
(11)
Тогда средняя задержка автотранспортного средства может быть вычислена следующим образом:
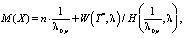 (12)
(12)
где n – количество полных циклов, проведенных АТС в ожидании возможности продолжить движение.
4. Расчет задержек пешеходов на переходе. Согласно предположению [7], распределение интервалов по времени между объектами (кластерами и отдельными «одиночными» пешеходами) подчиненяется показательному закону c параметром λ 0 p. Вычислим среднее время ожидания пешеходами возможности начать движение через дорогу. Поступим аналогично пункту 3.2.
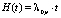 – функция восстановления для показательного закона (количество объектов, прибывших за время t).
– функция восстановления для показательного закона (количество объектов, прибывших за время t).
Разобьем интервал 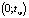 на n частей точками
на n частей точками 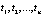 ;
; 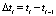 и вычислим суммарную задержку всех пешеходов, прибывающих к переходу за время tw. При этом каждый кластер отождествляем с одним объектом. Однако при нахождении средней задержки одного пешехода это будет учтено.
и вычислим суммарную задержку всех пешеходов, прибывающих к переходу за время tw. При этом каждый кластер отождествляем с одним объектом. Однако при нахождении средней задержки одного пешехода это будет учтено.
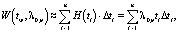
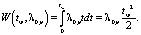 (13)
(13)
Среднее количество пешеходов, прибывающих к переходу, задает функция восстановления [8]. Пешеходы, прибывающие к переходу в то время, когда горит разрешающий сигнал, за редким исключением, перейдут дорогу, ускорив шаг, и будут заканчивать движение в течение времени tover. Следовательно, не будут тратить время на ожидание.
Таким образом, среднее время M(Tpc) ожидания возможности продолжить движение, задается формулой
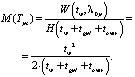 (14)
(14)
Заключение
Представленная выше модель движения транспортных и пешеходных потоков на переходах с вызывным устройством укладывается в рамки разработанной автором ранее модели распределения транспортных потоков по улично-дорожной сети. А следовательно, может увеличить диапазон транспортных задач, решаемых с ее помощью. Данный метод оценки проводится с помощью аналитических расчетов при ограниченном количестве исходных данных. Причем эти данные могут корректироваться по результатам, полученным с видеодетекторов. То есть разработанная модель вполне приемлема для использования в Интеллектуальных транспортных системах.
Библиографическая ссылка
Наумова Н.А., Карачанская Т.А. МОДЕЛЬ ОЦЕНКИ ЗАДЕРЖЕК АВТОТРАНСПОРТА И ПЕШЕХОДОВ НА ПЕРЕХОДАХ С ВЫЗЫВНЫМИ УСТРОЙСТВАМИ // Современные наукоемкие технологии. 2019. № 10-1. С. 68-72;URL: https://top-technologies.ru/ru/article/view?id=37699 (дата обращения: 05.03.2026).



