В период непосредственной угрозы агрессии и в военное время необходимо проведение комплекса мероприятий и действий по наращиванию и восполнению орбитальной группировки космических аппаратов военного назначения в стратегической космической зоне за короткий отрезок времени [1, 2]. Это в свою очередь приводит к резкому увеличению интенсивности запуска космических аппаратов (КА) военного назначения. Показателем, влияющим на оперативность наращивания и восполнения орбитальной группировки КА, является вероятность подготовки и пуска ракеты космического назначения (РКН) за заданное время (Рпп).
Анализ отчетов по пускам ракет-носителей «Союз-2» с 1-го Государственного испытательного космодрома Министерства обороны (МО) РФ показал, что в настоящее время имеется несоответствие вероятности подготовки и пуска РКН за заданное время требуемым значениям.
На эту вероятность оказывают влияние различные параметры системы обеспечения готовности (СОГ) РКН к пуску, такие как: количество запасных частей (ЗЧ) элементов замены (ЭЗ) технологического оборудования (ТлОБ) РКК; времена доставки ЗЧ ЭЗ; уровень обученности личного состава БР, характеризующийся временем устранения отказа tустр; период контроля технического состояния (ТС) ТлОб. Также стоит отметить, что эти параметры существенным образом влияют и на эксплуатационные затраты процесса подготовки РКН [3]. В свою очередь требованиями различных руководящих документов определена необходимость минимизации эксплуатационных затрат на вооружение и военную технику (ВВТ).
Таким образом вышесказанные обстоятельства свидетельствуют о необходимости наличия научно-методического аппарата, позволяющего выбрать оптимальные значения параметров СОГ, которые обеспечат требуемую Рпп при минимизации эксплуатационных затрат.
Целью данной статьи является представление на основе полученных зависимостей Рпп и эксплуатационных затрат от параметров СОГ [4] разработанной методики выбора таких их значений, которые позволят обеспечить требуемую вероятность подготовки и пуска РКН за заданное время при минимизации эксплуатационных затрат в условиях различной интенсивности запуска КА.
Структурно-логическая схема методики
Для того чтобы описать предложенную в статье методику выбора значений параметров СОГ РКН к пуску при различной интенсивности запусков КА, представим ее в виде структурно-логической схемы (рис. 1), на которой отражены основные ее этапы.
Определение оптимальных значений параметров сог ркн к пуску
Постановка задачи
В описанной выше методике наибольший интерес представляет этап 7, на котором происходит выбор оптимальных значений параметров СОГ РКН к пуску. Формально эта задача может быть представлена следующим образом:
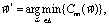(1)
где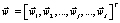 
– вектор параметров СОГ РКН к пуску; 
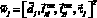– вектор параметров СОГ ТлОб, участвующего в проведении j-й ТехОп; 
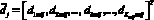– вектор, характеризующий количество ЗЧ k-го ЭЗ m-й СЧ i-го вида ТлОб, участвующего в j-й ТехОп; 
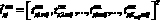– вектор, характеризующий ожидаемое время доставки ЗЧ k-го ЭЗ m-ой СЧ i-го вида ТлОб, участвующего в j-й ТехОп; 
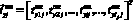– вектор, характеризующий ожидаемое время устранения отказа БР i-го вида ТлОб, участвующего в j-ой ТехОп; 
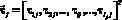– вектор, характеризующий периодичность контроля ТС i-го вида ТлОб, участвующего в j-й ТехОп; 
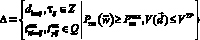– область допустимых значений параметров СОГ, учитывающая ограничения на 
и суммарный объем, отводимый для хранения ЗЧ (VTP).
Для решения представленной оптимизационной задачи был выбран метод динамического программирования [5]. Вместе с тем стоит отметить, решение задачи (1) с требуемой точностью вычислений будет затруднено необходимостью учета ограничения на вероятность подготовки и пуска РКН за заданное время, поэтому для решения этой частной задачи целесообразно, используя метод погружения, поставить более общую задачу (2), которая позволит в процессе однократного ее решения получить множество Парето-оптимальных решений, соответствующих возможным значениям пределов в ограничениях. Формально задача (2) может быть представлена в следующем виде:
Дано:
J, Ij, Mij, Kmij – данные о технологическом оборудовании, участвующем в процессе подготовки РКН; λkmij – интенсивность отказов ЭЗ ТлОб;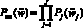 
– модель оценивания вероятности завершения процесса подготовки и пуска РКН за заданное время;
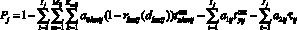– модель оценивания вероятности завершения j-й технологической операции за заданное время; 
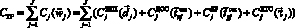– модель ресурсоемкости процесса подготовки и пуска ракеты космического назначения [2].
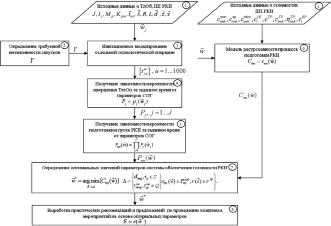
Рис. 1. Структурно-логическая схема методики выбора значений параметров системы обеспечения готовности РКН к пуску
Найти:
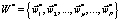– множество Парето-оптимальных решений, (2)
где
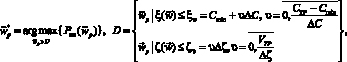
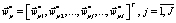– вектор условно-оптимальных решений, соответствующий паре 
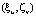; vkmij – объем, занимаемый ЗЧ k-го элемента замены m-й составной части i-го вида ТлОб, участвующего в j-й ТехОп.
Алгоритм решения задачи определения оптимальных значений параметров СОГ РКН к пуску
Для решения задачи (2) необходимо решить две последовательных задачи: Задача I – найти множество Парето-оптимальных решений для каждой операции ТГ; Задача II – путем «склейки» ТехОп, используя метод динамического программирования, найти множество Парето-оптимальных решений для всего процесса.
Решение Задачи I заключается в выполнении трех сложных в вычислительном плане шагов. Алгоритм первого шага представлен на рис. 2.
В результате выполнения описанного выше алгоритма (рис. 2) для всех значений 
и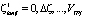 
получаем максимальное значение 
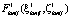и соответствующие ему условно-оптимальные значения количества ЗЧ – 
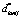и времени их доставки – 
.
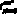Далее необходимо перейти к выполнению второго шага, блок-схема алгоритма которого приведена на рис. 3.
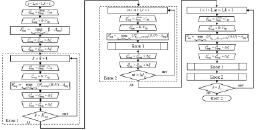
Рис. 2. Блок-схема алгоритма выполнения первого шага нахождения множества Парето-оптимальных решений для j-й ТехОп (с учетом количества ЗЧ ЭЗ и времен их доставки, где:
; 
;
; 
;
; 
;
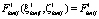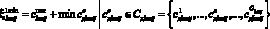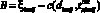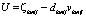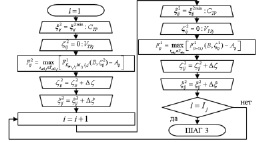
Рис. 3. Блок-схема алгоритма выполнения второго шага нахождения множества Парето-оптимальных решений для j-й ТехОп (с учетом времени устранения отказа), где:
; 
; 
; 
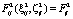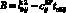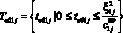
Результатом выполнения второго шага (рис. 3) является нахождение для всех значений 
и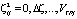 
максимального значения 
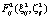и соответствующего ему условно-оптимального значения времени устранения отказа – 
.
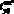Заключительным шагом нахождения множества Парето-оптимальных решений для j-ой ТехОп является 3 шаг. Блок-схема алгоритма его выполнения представлена на рис. 4.
В результате выполнения описанного выше алгоритма (рис. 4) для всех значений 
и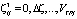 
получаем максимальное значение 
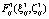и соответствующее ему условно-оптимальное значение периодичности контроля – 
.
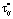Решение Задачи I J раз позволит получить множество Парето-оптимальных решений для каждой ТехОп технологического графика подготовки РКН к пуску и тем самым перейти к решению Задачи II – путем «склейки» ТехОп, используя метод динамического программирования, найти множество Парето-оптимальных решений для всего процесса.
Метод динамического программирования позволяет свести решение этой задачи с 2(J – 1) неизвестными к последовательному решению (J – 1) задачи с двумя неизвестными. При этом в связи с тем, что при решении каждой такой задачи неизвестно количество располагаемых денежных средств и суммарного объема, выделяемого для хранения ЗЧ, необходимо находить ее решение на первом шаге («склейка» первой и второй ТехОп) для всех возможных значений
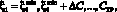(3)
где
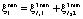
и для всех возможных значений
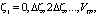(4)
а на втором и последующих шагах для всех возможных значений
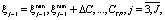(5)
где
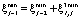
и для всех возможных значений
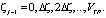(6)
Для первого шага функциональное уравнение Беллмана имеет вид
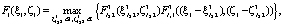(7)
где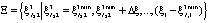 
, 
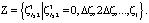
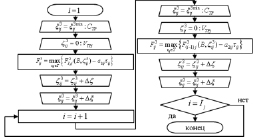
Рис. 4. Блок-схема алгоритма выполнения третьего шага нахождения множества Парето-оптимальных решений для j-ой ТехОп (с учетом периодичности контроля ТС), где:
; 
; 
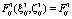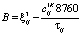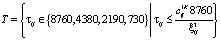
В результате выполнения этого шага получим для всех значений (3–4) максимальные значения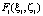 
и соответствующие им условно-оптимальные значения выделяемых денежных средств на проведение первой и второй ТехОп – 
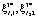и суммарных объемов, выделяемых для хранения ЗЧ – 
.
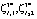Для последующих шагов (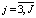
) уравнение Беллмана принимает следующий вид
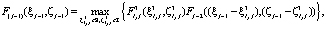(8)
где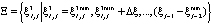 
, 
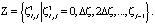
Результатом каждого шага является нахождение для всех значений (5–6) максимальных значений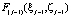 
и соответствующих им условно-оптимальных значений выделяемых денежных средств на j-ю ТехОп – 
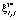и суммарных объемов, выделяемых для хранения ЗЧ – 
.
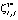Выполнив все шаги, получаем множество Парето-оптимальных решений для процесса подготовки РКН в целом.
Далее для решения обозначенной выше задачи (1) необходимо на последнем шаге выбрать условно-оптимальное значение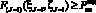 
при условие что соответствующее ему 
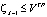, и, выполнив операции обратного хода, найти 
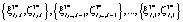. Затем для каждой пары 
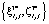, используя результаты решения задачи нахождения множества Парето-оптимальных решений для j-й ТехОп, также, выполнив операции обратного хода, найдем для нее вектор оптимальных значений параметров 
и в итоге вектор оптимальных значений параметров СОГ РКН к пуску –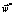 
.
Далее на основе полученного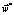 
будет возможна выработка практических рекомендаций и предложений по проведению комплекса мероприятий, направленного на обеспечение требуемой вероятности подготовки и пуска РКН за заданное время.
Заключение
В статье была описана методика выбора значений параметров системы обеспечения готовности РКН к пуску. Приведена структурно-логическая схема методики. Представлен алгоритм решения задачи определения оптимальных значений параметров СОГ РКН к пуску, но основе последовательного применения метода динамического программирования, на первом этапе которого удается получить множество Парето-оптимальных решений для каждой ТехОп технологического графика подготовки, а на втором – используя полученные решения, найти множество Парето-оптимальных решений для всего процесса подготовки РКН в целом.
Представленная методика выбора значений параметров системы обеспечения готовности РКН к пуску отличается от известных учетом различной интенсивности запуска КА военного назначения путем получения соответствующих значений коэффициентов регрессии модели оценивания вероятности завершения ТехОп за заданное время и позволяет выработать практические рекомендации и предложения по проведению комплекса мероприятий на основе полученного вектора оптимальных значений параметров СОГ РКН к пуску.
Библиографическая ссылка
Вивчарь Р.М., Решетников Д.В., Герасименко С.Ю. МЕТОДИКА ВЫБОРА ЗНАЧЕНИЙ ПАРАМЕТРОВ СИСТЕМЫ ОБЕСПЕЧЕНИЯ ГОТОВНОСТИ РАКЕТЫ КОСМИЧЕСКОГО НАЗНАЧЕНИЯ К ПУСКУ // Современные наукоемкие технологии. – 2019. – № 10-1. – С. 32-37;URL: https://top-technologies.ru/ru/article/view?id=37693 (дата обращения: 23.11.2024).