В сложившихся условиях конкуренции и постоянного развития новых технологий возникает проблема защиты информации путем ее преобразования, исключающего ее прочтение посторонним лицом. Создание квантовых компьютеров, технологий нейросетевых вычислений приводит к дискредитации некоторых криптографических систем.
Все системы шифрования можно разделить на два типа: симметричные и асимметричные системы шифрования. К первым относятся системы, в которых для шифрования и дешифрования используется один ключ. Ко вторым относятся системы, в которых для шифрования сообщения используется открытый ключ, а для дешифрования закрытый ключ. На данный момент наиболее распространенными являются асимметричные системы шифрования, которые позволяют решить проблему обмена ключами. Однако этот тип криптографических систем уступает по скорости и эффективности симметричным системам шифрования, которые могут быстро зашифровывать большие объемы данных.
Решением проблемы распространения ключа в симметричных системах шифрования занимались такие ученые, как А. Климов, А. Митягин, А. Шамир [1], Б.Р. Приянка [2], А. Мартин [3]. Ими было предложено использование криптографического алгоритма, основанного на синхронизации нейронных сетей.
Синхронизация представляет собой явление, которое можно наблюдать во многих физических и биологических системах. Она представляет интерес тем, что в результате ее достижения две и более системы приобретают одинаковые параметры. Синхронизацию нейронных сетей (далее НС) можно представить следующим образом: первоначально на вход НС поступают общие входные данные, являющиеся случайным набором, в дальнейшем при обучении в качестве входных данных выступают выходные значения других сетей [4]. Спустя короткое время достигается полная синхронизация, в результате которой весовые коэффициенты нейронных сетей оказываются равными. Полученные значения весовых коэффициентов в дальнейшем используются в качестве ключа шифрования.
Цель данного исследования заключалась в рассмотрении факторов, влияющих на скорость достижения синхронизации нейронных сетей в криптографическом алгоритме.
Архитектура TPM. В основе нейросетевой криптографии лежат TPM (tree parity machines – древовидные машины четности), которые являются многоуровневыми нейронными сетями прямого распространения [5]. Как показано на рис. 1, TPM имеет три слоя: входной, скрытый и выходной слой.
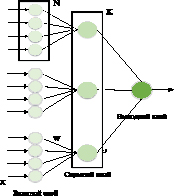
Рис. 1. Топология TPM
Рассматриваемая нейронная сеть, состоит из:
- K x N входных нейронов;
- K скрытых нейронов;
- одного скрытого нейрона.
Все входные значения являются случайными и двоичными значениями xi,j∈{–1, +1}, а веса – дискретными числами между –L и +L (где индекс i = 1, . . . ,К обозначает i-й скрытый нейрон, индекс j = 1, . . . N обозначает j-й входной нейрон, L – заданный параметр).
Как и в других НС, в TPM взвешенная сумма используется для определения выходных значений, а состояние скрытого нейрона определяется его суммарным входом
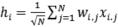 .
.
Выход каждого скрытого нейрона σi можно определить как
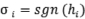 ,
,
а общий выход TPM задается произведением (четностью) скрытых единиц,
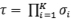 .
.
Основной концепцией синхронизации TPM является взаимное обучение. Процесс синхронизации начинается со случайно заданных входных векторов и случайно выбранных весовых коэффициентов. Обновление весов происходит только в том случае, если выходные значения двух TPM равны. Для достижения равенства весов необходимо выполнить следующие действия:
0. У двух абонентов есть многослойная сеть TPM.
1. Инициализация нейронной сети. В начале процесса синхронизации значения весовых коэффициентов задаются случайным образом.
2. Генерация случайного входного вектора, который подается на вход НС.
3. Вычисление значения скрытых и выходного нейронов.
4. Проверка равенства выходных значений обоих НС.
5. В случае несовпадения выходных значений необходимо вернуться ко второму шагу. Если выходные значения равны, тогда для каждой НС используем одно из трех правил обучений, представленных выше.
6. После достижения полной синхронизации НС на основе полученных весовых коэффициентов генерируется ключ шифрования [6].
Структура алгоритма синхронизации двух TPM представлена на рис. 2.
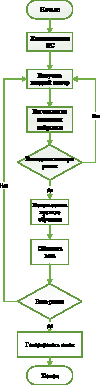
Рис. 2. Структура алгоритма синхронизации
Для достижения полной синхронизации древовидных машин четности можно использовать три правила обучения [7]:
- правило Хебба
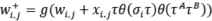 , (1)
, (1)
где wi,j – весовые значения скрытого слоя; xi,j – входные значения; τA – выходное значение TPMА; τB – выходное значение TPMВ; τ – общий выход.
- правило анти-Хебба
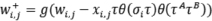 ; (2)
; (2)
- случайное блуждание [8]
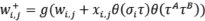 . (3)
. (3)
Представленные правила обучения должны гарантировать, нахождение весовых коэффициентов в допустимом диапазоне между –L и +L. Если же один из весов выходит за пределы этого промежутка, тогда он сбрасывается до ближайшего граничного значения L, что достигается путем использования функции g(w) в каждом правиле обучения.
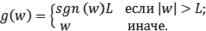
С учетом вышесказанного можно сделать вывод о том, что конечным результатом процесса синхронизации является получение одинаковых значений весовых коэффициентов двух НС.
Нейросетевая симметричная система шифрования на основе TPM. Рассмотрим, как можно использовать процесс синхронизации в предлагаемом криптографическом алгоритме. Оба участника связи (Алиса – отправитель, Боб – получатель) используют TPM, которые обладают одинаковой архитектурой. Такие параметры, как K, L и N, являются общедоступными.
Как уже было сказано, каждая нейронная сеть начинает процесс синхронизации со случайно выбранных весовых коэффициентов, которые держатся в секрете. В процессе синхронизации по общедоступному каналу связи передаются только входные значения xi и общие выходы τA и τB. Следовательно, каждый участник связи может знать только свое внутреннее представление (σ1, σ2, . . ., σК). После достижения полной синхронизации Алиса и Боб используют весовые коэффициенты в качестве общего секретного ключа.
На основе полученного секретного ключа Алиса и Боб могут использовать любой алгоритм симметричного шифрования. В общем виде процесс шифрования и дешифрования можно представить следующим образом:
Алиса шифрует исходное сообщение, используя закрытый ключ
E(m, d) = c,
где E – функция шифрования, d – закрытый ключ, m – открытый текст, с – зашифрованный текст.
Боб дешифрует полученное сообщение, используя тот же закрытый ключ
D(c, d) = m,
где D – функция дешифрования.
Безопасность. Безопасность криптографического алгоритма, основанного на процессе синхронизации, обеспечивается благодаря тому, что внутреннее представление TPM (σ1, σ2, ..., σК) неизвестно никому, кроме того участника связи, кому принадлежит эта нейронная сеть. Таким образом, для того чтобы расшифровать сообщение, злоумышленнику (Ева) надо знать состояния скрытых нейронов, поскольку от их значений зависит изменение весовых коэффициентов (уравнение 1, 2, 3).
Рассмотрим три метода атак, с помощью которых Ева может узнать секретный ключ:
- Метод перебора. Наиболее очевидным методом атаки на TPM является метод перебора. Однако данный способ является наименее эффективным, вследствие того, что необходимо перебрать тысячи комбинаций, прежде чем будет найдена правильная.
- Простая атака. Для осуществления этого типа атаки Ева использует TPM с такой же архитектурой, как у Алисы и Боба, а также входные xi и выходные τA значения. Как говорилось выше, эти значения передаются по общедоступному каналу связи. Ева так же, как Алиса и Боб, начинает синхронизацию со случайных весов. При этом Ева для обучения использует то же правило обучения, что Алиса и Боб. На каждом шаге возможны три ситуации: τA ≠ τB (веса не обновляются); τA = τB = τE (веса обновляются); τA = τB ≠ τE (веса обновляют Алиса и Боб). Таким образом, TPMЕ обучается медленнее, чем TPMА и TPMВ синхронизируются. Следовательно, Ева может определить ключ лишь с малой вероятностью.
- Генетическая атака. Данный тип атаки основан на эволюционном алгоритме, т.е. создании большой популяции TPM. Перед началом процесса синхронизации Ева имеет одну TPM с такой же архитектурой, как у Алисы и Боба. Всякий раз, когда Алиса и Боб обновляют веса (т.е. τA = τB), происходит следующее: пока число TPM, которыми обладает Ева, не превышает некоторый заданный порог M, то все TPMЕ заменяются на репрезентацию из F новых TPMЕ, каждая из которых получается альтернативной заменой скрытого нейрона на противоположное значение, собственно для этого подбираются новые веса [3].
Экспериментальная система и анализ результатов. На основе проведенного анализа был проведен эксперимент по сравнению представленных в первом разделе правил обучения TPM (правило Хебба, правило анти-Хебба, случайное блуждание). Целью эксперимента являлось определение того, как правила обучения влияют на продолжительность синхронизации двух TPM.
В качестве языка разработки экспериментальной системы был выбран Python, который представляет собой высокоуровневый язык программирования [9].
В экспериментальной системе были использованы четыре архитектуры TPM:
- K – 10; N – 5;
- K – 10; N – 25;
- K – 100; N – 10;
- K – 200; N – 15.
В таблице представлены параметры, полученные в ходе проведения эксперимента.
Параметры, полученные в ходе проведения эксперимента
|
Время сходимости, с |
Количество обновлений |
Количество обновлений, совершенных Евой |
|
|
Архитектура 10 х 5 |
|||
|
Правило Хебба |
0,193461 |
267 |
69 |
|
Правило анти-Хебба |
0,207788 |
314 |
92 |
|
Случайное блуждание |
0,092321 |
175 |
53 |
|
Архитектура 10 х 25 |
|||
|
Правило Хебба |
0,3806 |
322 |
72 |
|
Правило анти-Хебба |
0,5997 |
425 |
113 |
|
Случайное блуждание |
0,4255 |
320 |
92 |
|
Архитектура 100 х 10 |
|||
|
Правило Хебба |
3,67883 |
609 |
118 |
|
Правило анти-Хебба |
6,222801 |
1305 |
245 |
|
Случайное блуждание |
4,516365 |
897 |
146 |
|
Архитектура 200 х 15 |
|||
|
Правило Хебба |
16,745014 |
1187 |
214 |
|
Правило анти-Хебба |
39,21302 |
2723 |
576 |
|
Случайное блуждание |
23,25365 |
1469 |
272 |
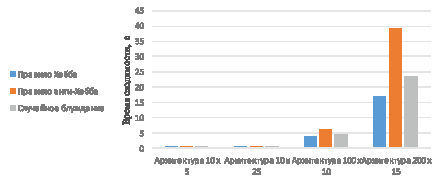
Рис. 3. Время, затраченное на синхронизацию (10×5)
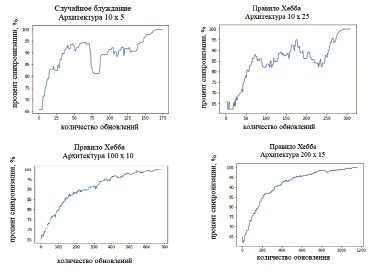
Рис. 4. Процесс синхронизации
На рис. 3 показано количество секунд, затраченных на синхронизацию TPMА и TPMВ с представленными выше архитектурами.
Рис. 4 демонстрирует, каким образом изменялась синхронизация TPMА и TPMВ в процессе обновления весов с использованием правил, показавших наименьшее время в результате проведенного эксперимента.
В результате проведенного эксперимента можно сделать вывод о том, что с увеличением количества нейронов во входном и скрытом слоях TPM эффективней использовать правило Хебба.
Выводы
Рассмотренный криптографический алгоритм, базирующийся на синхронизации двух нейронных сетей, позволяет решить проблему распространения секретного ключа в симметричных системах шифрования, к которым он относится. Однако данный алгоритм имеет два слабых места: он может быть взломан с помощью простой или генетической атаки. В качестве основного метода предотвращения простой атаки, который планируется исследовать в будущем, предлагаем использовать квантовые нейронные сети. Квантовые нейронные сети, основываясь на квантовых вычислениях, обладают такими преимуществами, как квантовый параллелизм, позволяющий работать одновременно со всеми допустимыми состояниями; теория о невозможности копирования неизвестного квантового состояния и невозможности прослушать сигнал, так как это искажает сообщение. Таким образом, можно сделать предположение о том, что криптографический алгоритм, основанный на использовании квантовых нейронных сетей, будет безопасным, вследствие невозможности прослушивания сигнала Евой. Для защиты от генетической атаки предлагаем исследовать возможность увеличения количества нейронов.
Библиографическая ссылка
Береза А.Н., Бегляров В.В., Шемякина М.А. КРИПТОГРАФИЧЕСКИЙ АЛГОРИТМ, ОСНОВАННЫЙ НА СИНХРОНИЗАЦИИ НЕЙРОННЫХ СЕТЕЙ // Современные наукоемкие технологии. 2019. № 10-1. С. 15-20;URL: https://top-technologies.ru/ru/article/view?id=37690 (дата обращения: 05.03.2026).



